二、感知机

感知机是二类分类的线性模型，属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分离超平面。是神经网络和支持向量机的基础。

• 模型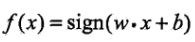：，w 叫作权值向量，b 叫做偏置，sign 是符号函数。
• 感知机的几何解释：wx+b 对应于特征空间中的一个分离超平面 S，其中 w 是 S 的法向量，b 是 S 的截距。S 将特征空间划分为两个部分，位于两个部分的点分别被分为正负两类。
• 策略：假设训练数据集是线性可分的，感知机的损失函数是误分类点到超平面 S 的总距离。因为误分类点到超平面S的距离是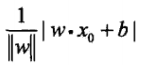，且对于误分类的数据来说，总有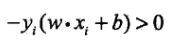成立，因此不考虑 1/||w||，就得到感知机的损失函数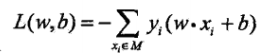：，其中 M 是误分类点的集合。感知机学习的策略就是选取使损失函数最小的模型参数。
• 算法：感知机的最优化方法采用随机梯度下降法。首先任意选取一个超平面 w0，b0，然后不断地极小化目标函数。在极小化过程中一次随机选取一个误分类点更新 w，b，直到损失函数为0。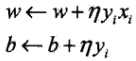其中 η 表示步长。该算法的直观解释是：当一个点被误分类，就调整 w，b 使分离超平面向该误分类点接近。感知机的解可以不同。
• 对偶原理：一个优化问题可以从主问题和对偶问题两个方面考虑。在推导对偶问题时，通过将拉格朗日函数对 x 求导并使导数为0来获得对偶函数。对偶函数给出了主问题最优解的下界，因此对偶问题一般是凸问题，那么只需求解对偶函数的最优解就可以了。
• 对偶形式：假设原始形式中的 w0 和 b0 均为0，设逐步修改 w 和 b 共 n 次，令 a=nη，最后学习到的 w，b 可以表示为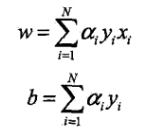那么对偶算法就变为设初始 a 和 b 均为0，每次选取数据更新 a 和 b 直至没有误分类点为止。对偶形式的意义在于可以将训练集中实例间的内积计算出来，存在 Gram 矩阵中，可以大大加快训练速度。