堆

什么是堆？

堆是一种特殊的完全二叉树。完全二叉树的含义就是每层节点都完全填满，除了最后一层外只允许最右边缺少若干个节点。在 JavaScript 中通常用数组表示堆（按照广度优先遍历顺序）。

最大堆

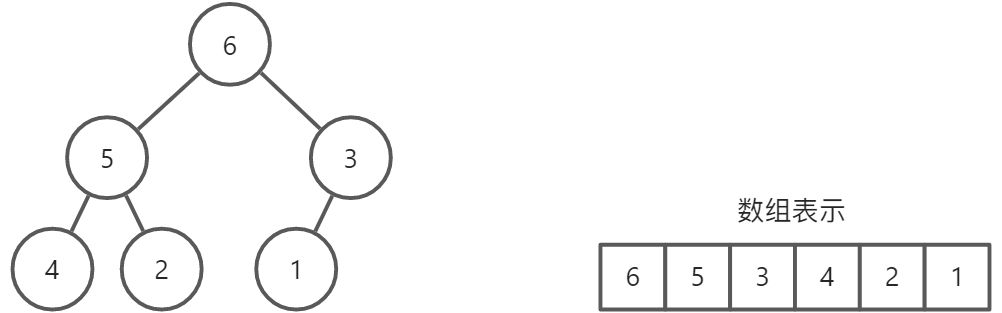
最小堆

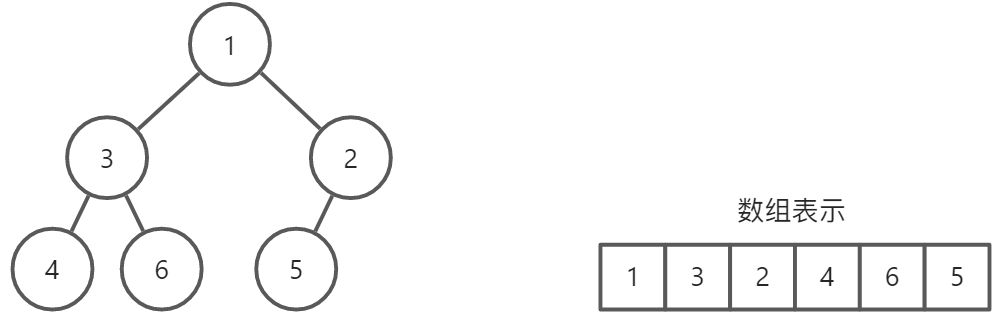
特性

• 所有的节点都大于等于它的子节点（最大堆）
• 或者所有的节点都小于等于它的子节点（最小堆）
• 左侧子节点的位置是 2 * index + 1
• 右侧子节点的位置是 2 * index + 2 （也就是在左子节点的基础上 + 1）
• 父节点的位置是 (index - 1) / 2

优点

• 高效、快速的找出堆的最大值和最小值，时间复杂度是 O (1)
• 找出第 K 个最大、最小元素

常用操作

插入：

• 将值插入堆的底部，即数据的尾部
• 然后上移，将这个值和它父节点进行交换，直到父节点小于等于这个插入的值
• 大小为 k 的堆中插入元素的时间复杂度为 O (logK)

删除堆顶：

• 用数组尾部元素替换堆顶（直接删除堆顶会破坏结构）
• 然后下移，将新堆顶和它的子节点进行交换，直到子节点大于等于这个新堆顶
• 大小为 k 的堆中删除堆顶的时间复杂度为 O (logK)

获取堆顶：

• 返回数组的第0项

获取堆大小：

• 返回数组的长度

案例

通过 Class 实现最小堆

class MinHeap {
    constructor() {
        this.heap = [];
    }
    top() {
        return this.heap[0];
    }
    size() {
        return this.heap.length;
    }
    getChildLeftIndex(i) {
        return i * 2 + 1;
    }
    getChildRightIndex(i) {
        return i * 2 + 2;
    }
    getParentIndex(i) {
        return (i - 1) >> 1;
    }
    swap(index1, index2) {
        const temp = this.heap[index1];
        this.heap[index1] = this.heap[index2];
        this.heap[index2] = temp;
    }
    shiftUp(index) {
        if (index === 0) return;
        const parentIndex = this.getParentIndex(index);
        if (this.heap[parentIndex] > this.heap[index]) {
            this.swap(parentIndex, index);
            this.shiftUp(parentIndex);
        }
    }
    shiftDown(index) {
        const leftChildIndex = this.getChildLeftIndex(index);
        const rightChildIndex = this.getChildRightIndex(index);
        if (this.heap[leftChildIndex] < this.heap[index]) {
            this.swap(leftChildIndex, index);
            this.shiftDown(leftChildIndex);
        }
        if (this.heap[rightChildIndex] < this.heap[index]) {
            this.swap(rightChildIndex, index);
            this.shiftDown(rightChildIndex);
        }
    }
    insert(value) {
        this.heap.push(value);
        this.shiftUp(this.heap.length - 1);
    }
    pop() {
        this.heap[0] = this.heap.pop();
        this.shiftDown(0);
    }
}
const h = new MinHeap();
h.insert(3);
h.insert(2);
h.insert(1);
h.pop()