LeetCode 417（太平洋大西洋流水问题）

解题步骤

1. 新建两个矩阵、分别记录能流到两个大洋的坐标
2. 从两个海岸线四个方向同时出发，进行深度优先遍历图，遍历过程中填充对应的两个矩阵
3. 遍历矩阵，找出能同时流到两个大洋的坐标

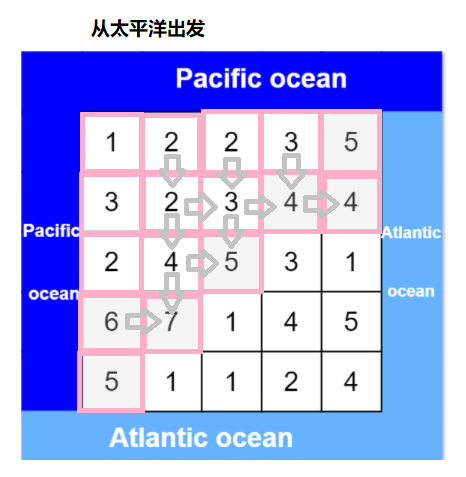
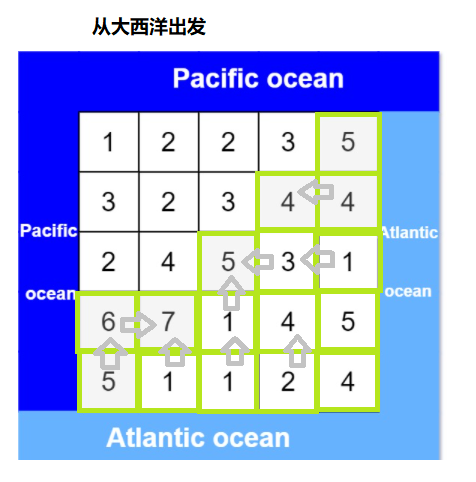
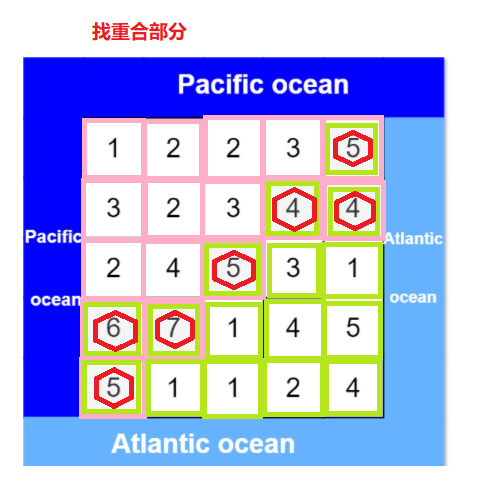
通过图的方式进行实现

• 时间复杂度：O (m * n)

• 空间复杂度：O (m * n)

  function pacificAtlantic(heights) {
    const rows = heights.length;
    const cols = heights[0].length;
    const matrix1 = Array.from({ length: rows }, () => new Array(cols).fill(false));
    const matrix2 = Array.from({ length: rows }, () => new Array(cols).fill(false));
    const dfs = (row, col, matrix) => {
        matrix[row][col] = true;
        [
            [row - 1, col],
            [row + 1, col],
            [row, col - 1],
            [row, col + 1],
        ].forEach(([nRow, nCol]) => {
            const cond1 = nRow >= 0 && nRow < rows && nCol >= 0 && nCol < cols;
            const cond2 = cond1 ? !matrix[nRow][nCol] : false;
            const cond3 = cond2 ? heights[row][col] <= heights[nRow][nCol] : false;
            if (cond1 && cond2 && cond3) {
                dfs(nRow, nCol, matrix);
            }
        });
    };
    for (let i = 0; i < rows; i++) {
        dfs(i, 0, matrix1);
        dfs(i, cols - 1, matrix2);
    }
    for (let i = 0; i < cols; i++) {
        dfs(0, i, matrix1);
        dfs(rows - 1, i, matrix2);
    }
    const res = [];
    for (let row = 0; row < rows; row++) {
        for (let col = 0; col < cols; col++) {
            if (matrix1[row][col] && matrix2[row][col]) {
                res.push([row, col]);
            }
        }
    }
    return res;
  }

上方代码中无论 for 循环写的多么复杂，但是我们实际上只是遍历了矩阵的每一个元素，所以时间复杂度是 O (m n)，m 代表是行的长度，n 是代表列的长度。代码中使用了两个矩阵，矩阵的大小是 m n 。所以我们按大的占用空间来算，空间复杂度是 O (m * n)。