什么是图?
图是网络结构的抽象模型,是一组由边连接的节点。图可以表示任何二元关系,比如道路、航班等。在 JavaScript 中没有图,但是可以通过 Object 和 Array 来构建图。
图的常用操作
- 深度优先遍历
- 广度优先遍历
图的表示法
- 邻接矩阵
- 邻接表
- 关联矩阵
- …
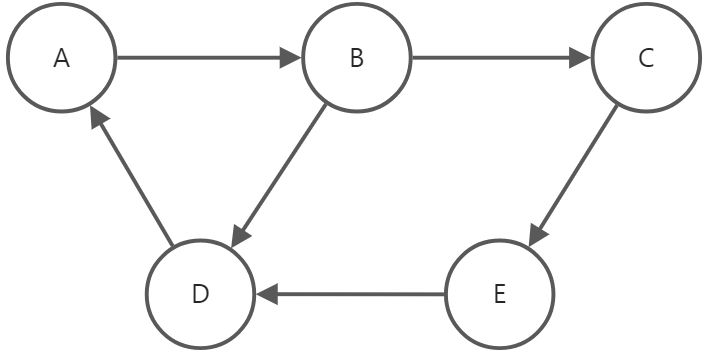
邻接矩阵:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 1 | 0 | 0 | 0 |
| ** | 0 | 0 | 1 | 1 | 0 |
| C | 0 | 0 | 0 | 0 | 1 |
| D | 1 | 0 | 0 | 0 | 0 |
| E | 0 | 0 | 0 | 1 | 0 |
邻接表:
并非仅限于通过数组表示,其他形式也可以。
{"A": ["B"],"B": ["C", "D"],"C": ["E"],"D": ["A"],"E": ["D"]}
图的深度/广度优先遍历
- 深度优先遍历
- 尽可能深的搜索图的分支
口诀:
- 先访问根节点
- 对根节点的没访问过的相邻节点挨个进行深度优先遍历(因为相邻节点可能也会指向当前节点)
const graph = {A: ['B'],B: ['C', 'D'],C: ['E'],D: ['A'],E: ['D'],};const visited = new Set();const dfs = (n) => {console.log(n);visited.add(n);graph[n].forEach((item) => {if (!visited.has(item)) {dfs(item);}});};dfs('A'); // A B C E D
广度优先遍历:
先访问离根节点最新的节点。
口诀:
- 新建一个队列,把根节点入队
- 把队头出队并访问
- 把队头的没有访问过的相邻节点入队
- 重复第2、3步直到队列为空
const graph = {A: ['B'],B: ['C', 'D'],C: ['E'],D: ['A'],E: ['D'],};const bfs = (head) => {const visited = new Set();visited.add(head);const q = [head];while (q.length) {const n = q.shift();console.log(n);graph[n].forEach((item) => {if (!visited.has(item)) {q.push(item);visited.add(item);}});}};bfs('A'); // A B C D E

