树的基础知识

递归遍历

中序遍历

public class InOrderTraversalRecursion {
    // 中序遍历
    public static List<Integer> inOrderTraversalRecursion(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inOrderDFS(root, result);
        return result;
    }
    private static void inOrderDFS(TreeNode node, List<Integer> result) {
        if (node == null) {
            return;
        }
        inOrderDFS(node.left, result);
        result.add(node.val);
        inOrderDFS(node.right, result);
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(inOrderTraversalRecursion(root));
    }
}

前序遍历

public class PreOrderTraversalRecursion {
    // 前序遍历
    public static List<Integer> preOrderTraversalRecursion(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        preOrderDFS(root, result);
        return result;
    }
    private static void preOrderDFS(TreeNode node, List<Integer> result) {
        if (node == null) {
            return;
        }
        result.add(node.val);
        preOrderDFS(node.left, result);
        preOrderDFS(node.right, result);
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(preOrderTraversalRecursion(root));
    }
}

后序遍历

public class PostOrderTraversalRecursion {
    // 后遍历
    public static List<Integer> preOrderTraversalRecursion(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        preOrderDFS(root, result);
        return result;
    }
    private static void preOrderDFS(TreeNode node, List<Integer> result) {
        if (node == null) {
            return;
        }
        preOrderDFS(node.left, result);
        preOrderDFS(node.right, result);
        result.add(node.val);
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(preOrderTraversalRecursion(root));
    }
}

迭代+栈

中序遍历

public class InOrderTraversal {
    // 中序遍历
    public static List<Integer> inOrderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            // DFS
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            // 中序遍历
            result.add(cur.val);
            // 处理右侧节点
            cur = cur.right;
        }
        return result;
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(inOrderTraversal(root));
    }
}

前序遍历

public class PreOrderTraversal {
    // 前序遍历
    public static List<Integer> preOrderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            // DFS
            while (cur != null) {
                // 前序遍历
                result.add(cur.val);
                // dfs
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            // 处理右侧节点
            cur = cur.right;
        }
        return result;
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(preOrderTraversal(root));
    }
}

后序遍历

public class PostOrderTraversal {
    // 后续遍历
    public static List<Integer> postOrderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode pre = null;
        while (cur != null || !stack.isEmpty()) {
            // DFS
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            // peek 栈顶，不是pop哦，
            cur = stack.peek();
            if (cur.right != null && cur.right != pre) {
                // 如果右子树还没被遍历，则外循环先遍历右子树
                cur = cur.right;
            } else {
                // 遍历当前节点
                result.add(cur.val);
                // 后序遍历，此时当前节点的子节点都遍历完了，可以pop掉
                stack.pop();
                // 更新pre节点
                pre = cur;
                // 置空cur节点，待下一轮循环pop出来
                cur = null;
            }
        }
        return result;
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(postOrderTraversal(root));
    }
}

二叉树的深度优先搜索

47：二叉树剪枝

:::info 题目：一棵二叉树的所有节点的值要么是0要么是1，请剪除该二叉树中所有节点的值全都是0的子树。例如，在剪除图8.2（a）中二叉树中所有节点值都为0的子树之后的结果如图8.2（b）所示。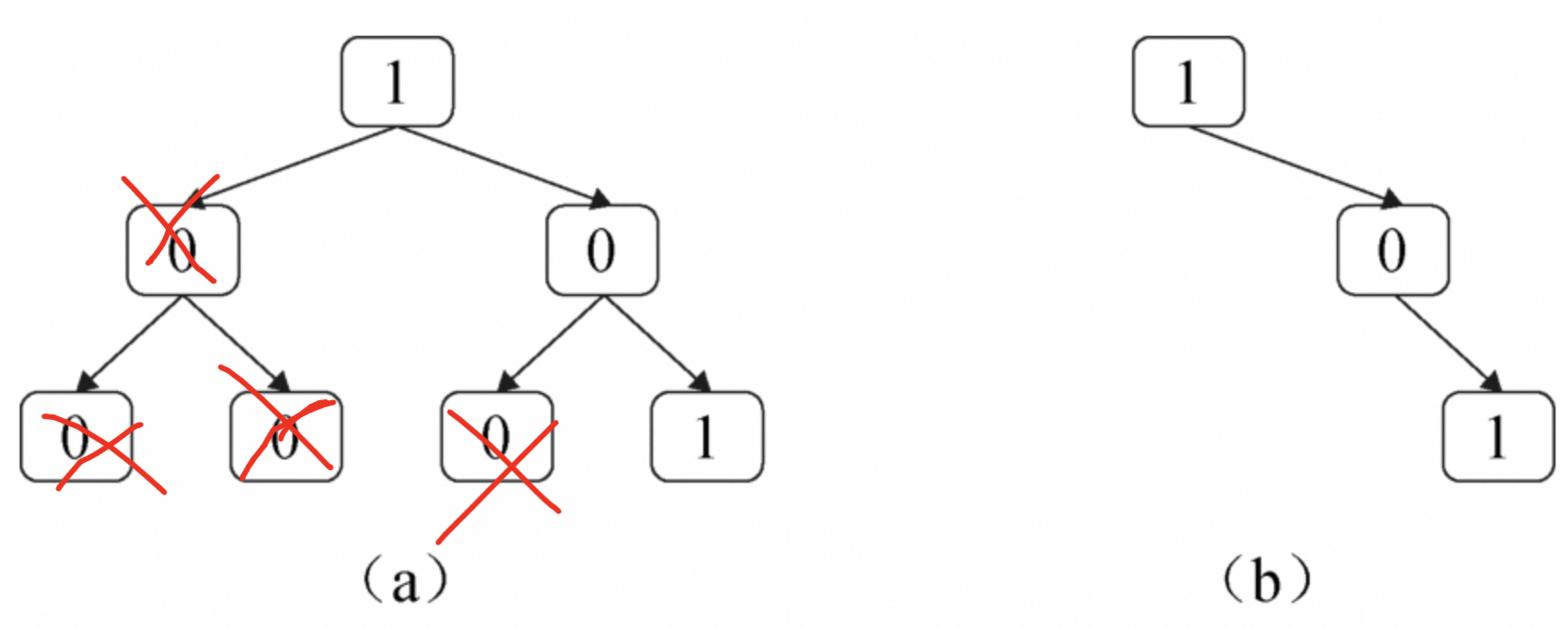
:::

public class PruneTree {
    public static TreeNode pruneTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        // 递归处理左子树
        root.left = pruneTree(root.left);
        // 递归处理左子树
        root.right = pruneTree(root.right);
        // 如果当前节点是叶子节点，且值为0，那它可以被剪去
        if (root.left == null && root.right == null && root.val == 0) {
            // 从递归的视角看，
            // 由于是后续遍历，如果一个节点的子节点都是0，那么当递归遍历到自己的时候，它的子节点都已经被剪完了，也可以被剪去
            return null;
        }
        return root;
    }
}

48：序列化和反序列化二叉树

:::info 题目：请设计一个算法将二叉树序列化成一个字符串，并能将该字符串反序列化出原来二叉树的算法。 :::

public class SerializeBinaryTree {
    /**
     * 前序遍历二叉树，null节点用#补齐
     * @param root
     * @return
     */
    public static String serializeBinaryTree(TreeNode root) {
        if (root == null) {
            return "#";
        }
        String leftString = serializeBinaryTree(root.left);
        String rightString = serializeBinaryTree(root.right);
        return root.val + "," + leftString + "," + rightString;
    }
    public static TreeNode deserializeBinaryTree(String string) {
        String[] arr = string.split(",");
        int[] index = {0};
        return deserializeBinaryTree(arr, index);
    }
    /**
     * 由于是前序遍历， 所以当前节点就是父节点，然后再分别递归处理左子树和右子树
     * 递归的终止条件是遇到"#"空节点时，返回null
     * @param arr
     * @param index
     * @return
     */
    private static TreeNode deserializeBinaryTree(String[] arr, int[] index) {
        String val = arr[index[0]];
        index[0]++;
        if (val.equals("#")) {
            return null;
        }
        TreeNode node = new TreeNode(Integer.valueOf(val));
        node.left = deserializeBinaryTree(arr, index);
        node.right = deserializeBinaryTree(arr, index);
        return node;
    }
}

49：从根节点到叶节点的路径数字之和

:::info 题目：在一棵二叉树中所有节点都在0～9的范围之内，从根节点到叶节点的路径表示一个数字。求二叉树中所有路径表示的数字之和。例如，图8.4的二叉树有3条从根节点到叶节点的路径，它们分别表示数字395、391和302，这3个数字之和是1088。 :::

public class PathSum {
    public static int pathSum(TreeNode root) {
        return pathSum(0, root);
    }
    public static int pathSum(int sum, TreeNode node) {
        if (node == null) {
            return 0;
        }
        sum = sum * 10 + node.val;
        // 如果是叶子节点，此时要终止。
        // 上一句已经加过了，不然走到下面又多加一次
        // PS：递归的理解可真难orz
        if (node.left == null && node.right == null) {
            return sum;
        }
        // sum是int，是值传递，所以不会影响其他节点的递归
        return pathSum(sum, node.left) + pathSum(sum, node.right);
    }
}

50：向下的路径节点值之和

:::info 题目：给定一棵二叉树和一个值sum，求二叉树中节点值之和等于sum的路径的数目。路径的定义为二叉树中顺着指向子节点的指针向下移动所经过的节点，但不一定从根节点开始，也不一定到叶节点结束。例如，在如图8.5所示中的二叉树中有两条路径的节点值之和等于8，其中，第1条路径从节点5开始经过节点2到达节点1，第2条路径从节点2开始到节点6。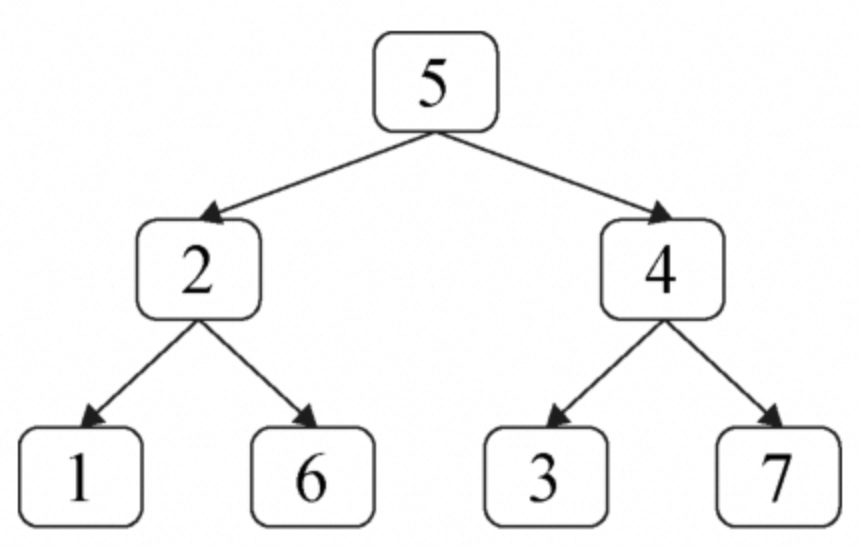
:::

public class pathSum50 {
    public static int pathsum(TreeNode root, int sum) {
        // 累加和，count
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0, 1);
        int pathSum = 0;
        return dfs(root, map, sum, pathSum);
    }
    private static int dfs(TreeNode node, Map<Integer, Integer> map, int sum, int pathSum) {
        if (node == null) {
            return 0;
        }
        pathSum += node.val;
        int count = map.getOrDefault(pathSum - sum, 0);
        map.put(pathSum, map.getOrDefault(pathSum, 0) + 1);
        count += dfs(node.left, map, sum, pathSum);
        count += dfs(node.right, map, sum, pathSum);
        // 此时当前节点的左右字数都遍历完了，count已经计算上了
        // 就把自己的累计值从map里面去掉，这样不影响其他路径的计算
        map.put(pathSum, map.get(pathSum) - 1);
        return count;
    }
}

51：节点值之和最大的路径

:::info 题目：在二叉树中将路径定义为顺着节点之间的连接从任意一个节点开始到达任意一个节点所经过的所有节点。路径中至少包含一个节点，不一定经过二叉树的根节点，也不一定经过叶节点。给定非空的一棵二叉树，请求出二叉树所有路径上节点值之和的最大值。例如，在如图8.6所示的二叉树中，从节点15开始经过节点20到达节点7的路径的节点值之和为42，是节点值之和最大的路径。 :::

// TODO

二叉搜索树

// TODO

我是一个程序猿

chapter8 树

树的基础知识

递归遍历

中序遍历

前序遍历

后序遍历

迭代+栈

中序遍历

前序遍历

后序遍历

二叉树的深度优先搜索

47：二叉树剪枝

48：序列化和反序列化二叉树

49：从根节点到叶节点的路径数字之和

50：向下的路径节点值之和

51：节点值之和最大的路径

二叉搜索树

TreeSet和TreeMap的应用