队列的应用

41：滑动窗口的平均值

:::info 请实现如下类型MovingAverage，计算滑动窗口中所有数字的平均值，该类型构造函数的参数确定滑动窗口的大小，每次调用成员函数next时都会在滑动窗口中添加一个整数，并返回滑动窗口中所有数字的平均值。 :::

public class MovingAverage {
    private Queue<Integer> queue = new LinkedList<>();
    int sum = 0;
    int capcity = 0;
    public MovingAverage(int capacity) {
        this.capcity = capacity;
    }
    public double next(int val) {
        if (queue.size() == capcity) {
            int deletedNum = queue.poll();
            sum -= deletedNum;
        }
        sum += val;
        queue.add(val);
        return (double) sum / queue.size();
    }
    public static void main(String[] args) {
        MovingAverage movingAverage = new MovingAverage(3);
        System.out.println(movingAverage.next(1));
        System.out.println(movingAverage.next(2));
        System.out.println(movingAverage.next(3));
        System.out.println(movingAverage.next(4));
    }
}

42：最近请求次数

:::info 题目：请实现如下类型RecentCounter，它是统计过去3000ms内的请求次数的计数器。该类型的构造函数RecentCounter初始化计数器，请求数初始化为0；函数ping（int t）在时间t添加一个新请求（t表示以毫秒为单位的时间），并返回过去3000ms内（时间范围为[t-3000，t]）发生的所有请求数。假设每次调用函数ping的参数t都比之前调用的参数值大。 :::

public cleass RecentCounter {
    private int windowSize = 3000;
    private Queue<Integer> times = new LinkedList<>();
    public RecentCounter42() {
    }
    public int ping(int time) {
        times.offer(time);
        while(times.peek() + windowSize < time) {
            times.poll();
        }
        return times.size();
    }
}

二叉树的广度优先搜索

BFS

:::info 二叉树的广度优先遍历 :::

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int val) {
        this.val = val;
    }
}

public class BFS {
    public void bfd(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if(root == null) {
            return result;
        }
        queue.add(root);
        while(queue.isNotEmpty()) {
            TreeNode node = queue.poll();
            result.add(node.val);
            if(node.left != null) {
                queue.offer(left);
            }
            if(node.right != null) {
                queue.offer(right);
            }
        }
        return result;
    }
    public static void main(String[] args) {
        TreeNode node5 = new TreeNode(5);
        TreeNode node7 = new TreeNode(7);
        TreeNode node6 = new TreeNode(6, node5, node7);
        TreeNode node9 = new TreeNode(9);
        TreeNode node11 = new TreeNode(11);
        TreeNode node10 = new TreeNode(10, node9, node11);
        TreeNode node8 = new TreeNode(8, node6, node10);
        System.out.println(bfs(node8));
    }
}

:::info 笔记：
队列的特点是先进先出，所以每一层的元素先进队列之后，一定会先被遍历到，才会开始遍历后进的子节点。 :::

43：在完全二叉树中添加节点

:::info 题目：在完全二叉树中，除最后一层之外其他层的节点都是满的（第n层有2n-1个节点）。最后一层的节点可能不满，该层所有的节点尽可能向左边靠拢。例如，图7.3中的4棵二叉树均为完全二叉树。实现数据结构CBTInserter有如下3种方法。
● 构造函数CBTInserter（TreeNode root），用一棵完全二叉树的根节点初始化该数据结构。
● 函数insert（int v）在完全二叉树中添加一个值为v的节点，并返回被插入节点的父节点。例如，在如图7.3（a）所示的完全二叉树中添加一个值为7的节点之后，二叉树如图7.3（b）所示，并返回节点3。在如图7.3（b）所示的完全二叉树中添加一个值为8的节点之后，二叉树如图7.3（c）所示，并返回节点4。在如图7.3（c）所示的完全二叉树中添加节点9会得到如图7.3（d）所示的二叉树并返回节点4。
● 函数get_root()返回完全二叉树的根节点。 :::

public class CBTInserter {
    // 保存所有左右子节点不完全的节点
    private Queue<TreeNode> queue = new LinkedList<>();
    private TreeNode root;
    public CBTInserter(TreeNode treeNode) {
        this.root = treeNode;
        if (treeNode != null) {
            queue.offer(treeNode);
            // 遍历直到找到最后一层不满的节点
            while (queue.peek().left != null && queue.peek().right != null) {
                TreeNode node = queue.poll();
                queue.offer(node.left);
                queue.offer(node.right);
            }
        }
    }
    public int insert(TreeNode node) {
        queue.offer(node);
        TreeNode parent = queue.peek();
        if (parent.left == null) {
            parent.left = node;
        } else {
            parent.right = node;
            // 右节点补齐了，要把这个节点从queue里面删掉了
            queue.poll();
            queue.offer(parent.left);
            queue.offer(parent.right);
        }
        return parent.val;
    }
    public TreeNode getRoot() {
        return root;
    }
    public static void main(String[] args) {
        TreeNode node4 = new TreeNode(4);
        TreeNode node5 = new TreeNode(5);
        TreeNode node2 = new TreeNode(2, node4, node5);
        TreeNode node6 = new TreeNode(6);
        TreeNode node7 = new TreeNode(7);
        TreeNode node3 = new TreeNode(3, node6, node7);
        TreeNode node1 = new TreeNode(1, node2, node3);
        CBTInserter inserter = new CBTInserter(node1);
        System.out.println(inserter.insert(new TreeNode(8)));
        System.out.println(inserter.insert(new TreeNode(9)));
        System.out.println(inserter.insert(new TreeNode(10)));
    }
}

44：二叉树中每层的最大值

:::info 题目：输入一棵二叉树，请找出二叉树中每层的最大值。例如，输入图7.4中的二叉树，返回各层节点的最大值[3，4，9]。

:::

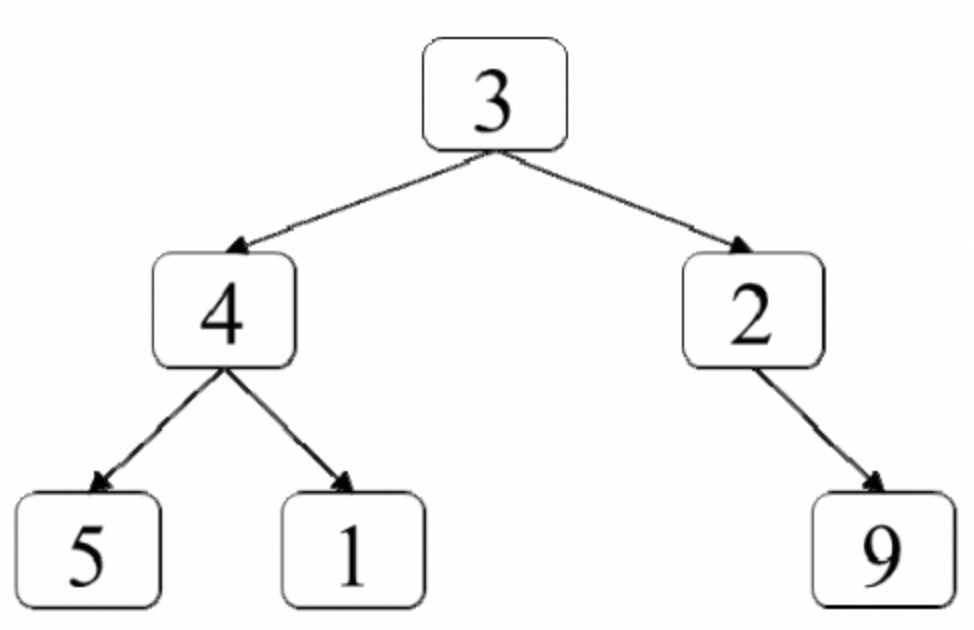public class LargestValues{
    public static List<Integer> findLargestValues(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<Integer> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int current = 1;
        int next = 0;
        int maxValue = Integer.MIN_VALUE;
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            maxValue = Math.max(maxValue, node.val);
            current--;
            if (node.left != null) {
                queue.offer(node.left);
                next++;
            }
            if (node.right != null) {
                queue.offer(node.right);
                next++;
            }
            // 这个if条件需要放在最后，否则next的计数会不准确
            if (current == 0) {
                result.add(maxValue);
                // 重置计数器
                maxValue = Integer.MIN_VALUE;
                current = next;
                next = 0;
            }
        }
        return result;
    }
    public static List<Integer> findLargestValuesWith2Queue(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<Integer> result = new ArrayList<>();
        // 用来存当前层
        Queue<TreeNode> queue1 = new LinkedList<>();
        queue1.offer(root);
        // 用来存下一层
        Queue<TreeNode> queue2 = new LinkedList<>();
        Integer maxValue = Integer.MIN_VALUE;
        while (!queue1.isEmpty()) {
            TreeNode node = queue1.poll();
            maxValue = Math.max(maxValue, node.val);
            if (node.left != null) {
                queue2.offer(node.left);
            }
            if (node.right != null) {
                queue2.offer(node.right);
            }
            // 这个if条件需要放在最后
            if (queue1.isEmpty()) {
                result.add(maxValue);
                queue1 = queue2;
                queue2 = new LinkedList<>();
            }
        }
        return result;
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(findLargestValues(root));
        System.out.println(findLargestValuesWith2Queue(root));
    }
}

45：二叉树最低层最左边的值

:::info 题目：如何在一棵二叉树中找出它最低层最左边节点的值？假设二叉树中最少有一个节点。例如，在如图7.5所示的二叉树中最低层最左边一个节点的值是5。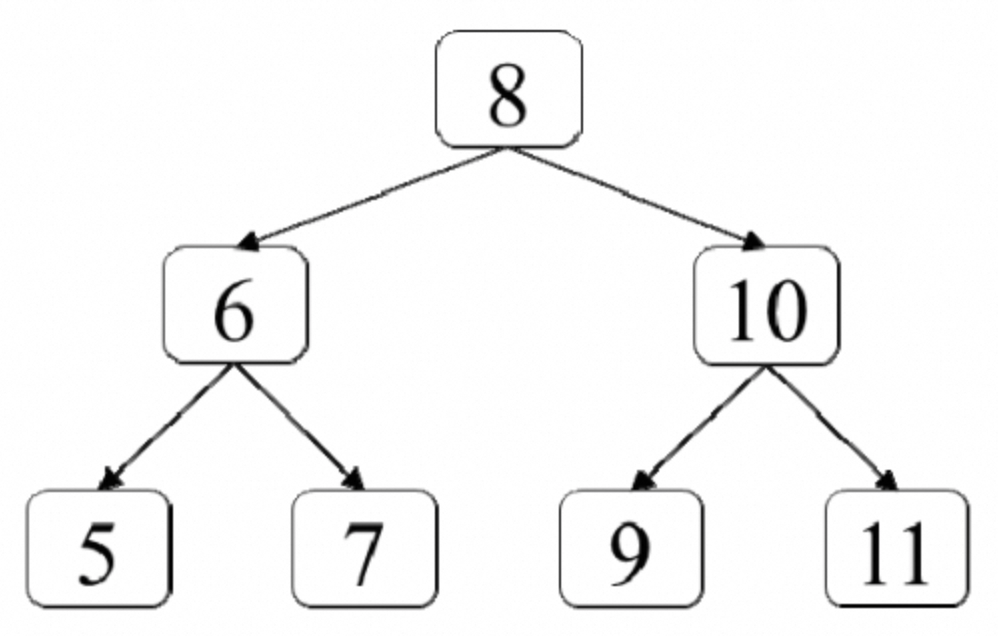
:::

public class BottomLeft {
    public static TreeNode findBottomLeftNode(TreeNode root) {
        if (root == null) {
            return null;
        }
        List<Integer> result = new ArrayList<>();
        // 用来存当前层
        Queue<TreeNode> queue1 = new LinkedList<>();
        queue1.offer(root);
        // 用来存下一层
        Queue<TreeNode> queue2 = new LinkedList<>();
        TreeNode bottomLeftNode = root;
        while (!queue1.isEmpty()) {
            TreeNode node = queue1.poll();
            if (node.left != null) {
                queue2.offer(node.left);
            }
            if (node.right != null) {
                queue2.offer(node.right);
            }
            // 这个if条件需要放在最后
            if (queue1.isEmpty()) {
                if (!queue2.isEmpty()) {
                    bottomLeftNode = queue2.peek();
                }
                queue1 = queue2;
                queue2 = new LinkedList<>();
            }
        }
        return bottomLeftNode;
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(findBottomLeftNode(root).val);
    }
}

46：二叉树的右侧视图

:::info 题目：给定一棵二叉树，如果站在该二叉树的右侧，那么从上到下看到的节点构成二叉树的右侧视图。例如，图7.6中二叉树的右侧视图包含节点8、节点10和节点7。请写一个函数返回二叉树的右侧视图节点的值。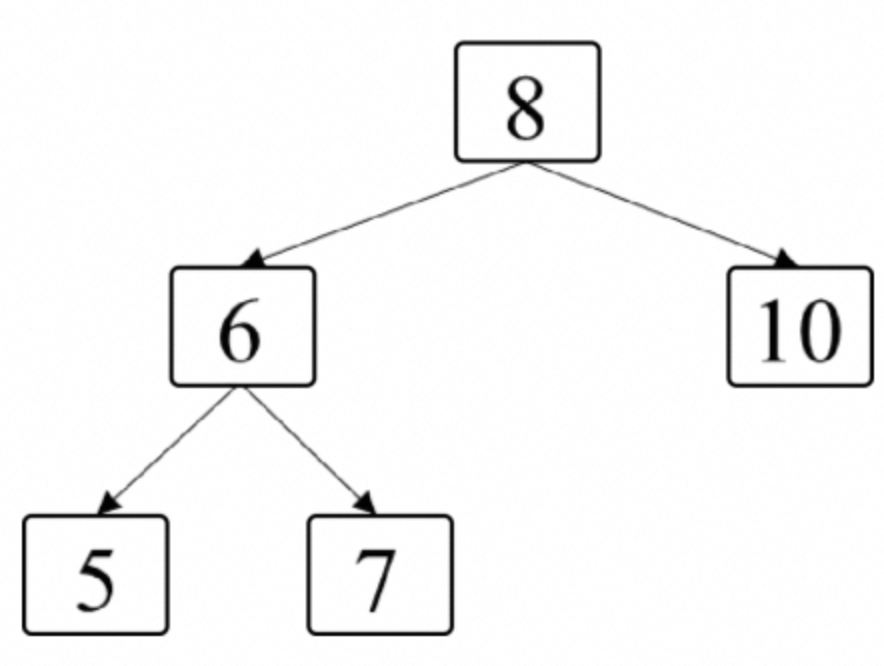
:::

public class RightView {
    public static List<Integer> rightView(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<Integer> result = new ArrayList<>();
        // 用来存当前层
        Queue<TreeNode> queue1 = new LinkedList<>();
        queue1.offer(root);
        // 用来存下一层
        Queue<TreeNode> queue2 = new LinkedList<>();
        while (!queue1.isEmpty()) {
            TreeNode node = queue1.poll();
            if (node.left != null) {
                queue2.offer(node.left);
            }
            if (node.right != null) {
                queue2.offer(node.right);
            }
            // 这个if条件需要放在最后
            if (queue1.isEmpty()) {
                result.add(node.val);
                queue1 = queue2;
                queue2 = new LinkedList<>();
            }
        }
        return result;
    }
    public static void main(String[] args) {
        TreeNode root = TreeNode.buildCBT();
        System.out.println(rightView(root));
    }

我是一个程序猿

chapter7 队列