Leetcode240.搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        for(int i = 0; i< m; i++){
            for(int j = 0; j< n; j++){
                if(matrix[i][j]>target){
                    break;
                }else if(matrix[i][j] == target){
                    return true;
                }
            }
        }
        return false;

    }
}

一点脑子没动，虽然通过了

参考题解（二分查找）：
每一行左边是最小的，右边是最大的
①如果某一行的第一个元素大于target，那么直接结束返回false
②如果某一行的最后一个元素小于target，那么continue跳过，下一行继续搜索
③每一行利用二分查找

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if(matrix.length == 0 ||  matrix[0].length == 0){
            return false;
        }
        for(int i = 0; i<matrix.length; i++){
            if(matrix[i][0]>target){
                break;
            }
            if(matrix[i][matrix[i].length - 1]<target){
                continue;
            }
            int col = binarySearch(matrix[i], target);
            if(col!=-1){
                return true;
            }
        }
        return false;
}
private int binarySearch(int[] nums, int target){
    int start = 0;
    int end = nums.length - 1;
    while(start<=end){
        int mid = (start + end)/2;
        if(nums[mid] == target ){
            return mid;
        }else if(nums[mid]>target){
            end = mid -1;
        }else if(nums[mid]<target){
            start = mid +1;
        }
    }
    return -1;
}
}

题解三（找规律，二叉树）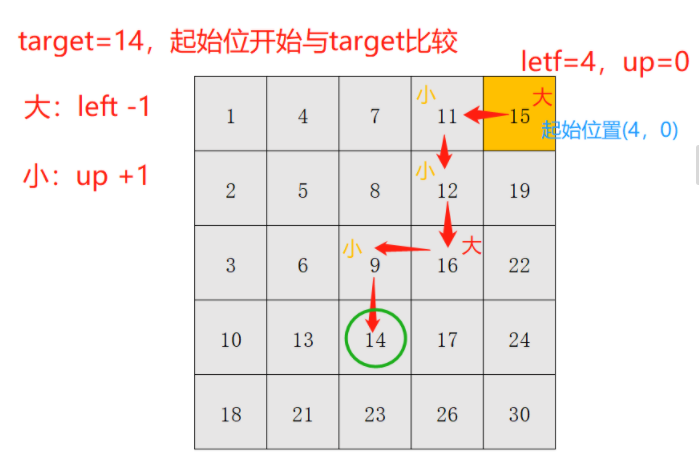

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
       if(matrix.length == 0 || matrix[0].length ==0){
           return false;
       }
       int right = matrix[0].length - 1;
       int up = 0;
       while(right>=0&&up<=matrix.length - 1){
           if(matrix[up][right] == target){
               return true;
           }else if(matrix[up][right] > target){
               right --;
           }else{
               up++;
           }
       }
       return false;
}
}