给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [0]
输出:0
示例 4:
输入:nums = [-1]
输出:-1
示例 5:
输入:nums = [-100000]
输出:-100000
提示:
1 <= nums.length <= 3 * 104
-105 <= nums[i] <= 105
题解:
首先我们分析题目,一个连续子数组一定要以一个数作为结尾,那么我们可以将状态定义成如下:
dp[i]:表示以 nums[i] 结尾的连续子数组的最大和。
那么为什么这么定义呢?因为这样定义其实是最容易想到的!在上一节中我们提到,状态转移方程其实是通过1-3个参数的方程来描述小规模问题和大规模问题间的关系。
当然,如果你没有想到,其实也非常正常!因为该问题最早于 1977 年提出,但是直到 1984 年才被发现了线性时间的最优解法。
根据状态的定义,我们继续进行分析:如果要得到 dp[i],那么 nums[i] 一定会被选取。并且 dp[i] 所表示的连续子序列与 dp[i-1] 所表示的连续子序列很可能就差一个 nums[i] 。即:
dp[i] = dp[i-1]+nums[i] , if (dp[i-1] >= 0)
但是这里我们遇到一个问题,很有可能 dp[i-1] 本身是一个负数。那这种情况的话,如果 dp[i] 通过 dp[i-1]+nums[i] 来推导,那么结果其实反而变小了,因为我们 dp[i] 要求的是最大和。所以在这种情况下,如果 dp[i-1] < 0,那么 dp[i] 其实就是 nums[i] 的值。即
dp[i] = nums[i] , if (dp[i-1] < 0)
综上分析,我们可以得到:
dp[i]=max(nums[i], dp[i−1]+nums[i])
得到了状态转移方程,但是我们还需要通过一个已有的状态的进行推导,我们可以想到 dp[0] 一定是以 nums[0] 进行结尾,所以
dp[i] = dp[i-1]+nums[i] , if (dp[i-1] >= 0)
dp[0] = nums[0]
在很多题目中,因为 dp[i] 本身就定义成了题目中的问题,所以 dp[i] 最终就是要的答案。但是这里状态中的定义,并不是题目中要的问题,不能直接返回最后的一个状态 (这一步经常有初学者会摔跟头)。所以最终的答案,其实我们是寻找:
max(dp[0], dp[1], …, d[i-1], dp[i])
分析完毕,我们绘制成图(图中假定 nums 为 [-2,1,-3,4,-1,2,1,-5,4]):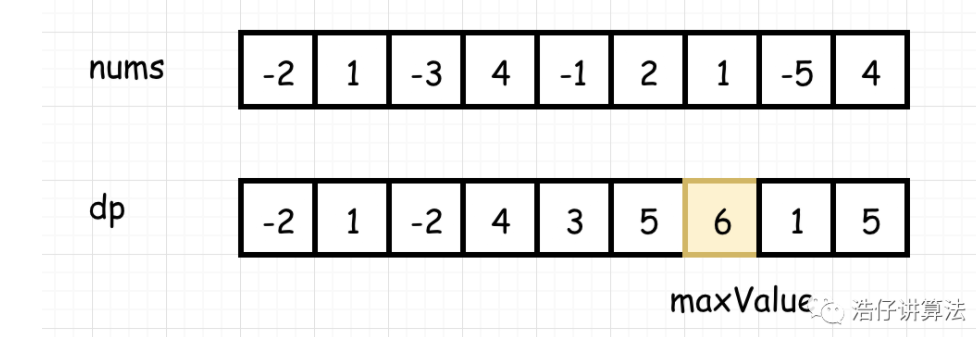
class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];for(int i = 1; i<nums.length; i++){if(dp[i-1]>0){dp[i] = dp[i-1] +nums[i];}else{dp[i] = nums[i];}}int res = dp[0];for(int i = 1; i<dp.length; i++){res = Math.max(res, dp[i]);}return res;}}

