Leetcode104. 二叉树的最大深度

https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

3<br />   / \<br />  9  20<br />    /  \<br />   15   7<br />返回它的最大深度 3 。

递归（DFS）：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
              if(root == null){
                  return 0;
              }
              int max = 0;
              int maxL = 0;
              int maxR = 0;
              //左子树深度
              maxL = maxDepth(root.left);
              //右子树深度
              maxR = maxDepth(root.right);
              max = maxL>maxR?maxL+1:maxR+1;
              return max;
    }
}

把握一点，树的深度 = max(左子树深度，右子树深度)+1
终止条件：当前为空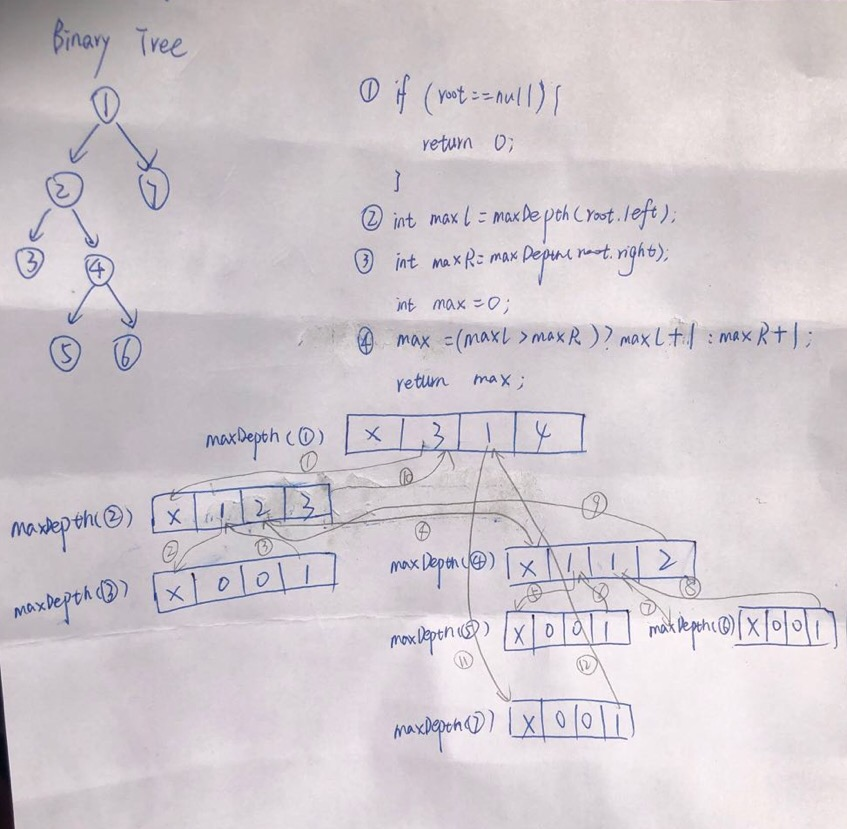

复杂度分析
时间复杂度：O(n), 我们每个结点只访问一次，因此时间复杂度为 O(N)
空间复杂度：
最坏情况下，树是完全不平衡的，例如每个结点只剩下左子结点，递归将会被调用 N 次（树的高度），因此保持调用栈的存储将是 O(N)。
最好情况下（树是完全平衡的），树的高度将是 log(N)。因此，在这种情况下的空间复杂度将是 O(log(N))

迭代（BFS）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;
        while(!queue.isEmpty()){
            int n = queue.size();
            while(n>0){
                TreeNode node = queue.poll();
                n -- ;
                if(node.left!=null){
                    queue.offer(node.left);
                }
                if(node.right!=null){
                    queue.offer(node.right);
                }
            }
            depth ++;
        }
    return depth;
    }
}

实际就是树的层次遍历代码每层的节点从队列全部弹出后，depth++

• 时间复杂度：O(n)
• 空间复杂度：O(width)，树的宽度，最坏情况O(n)