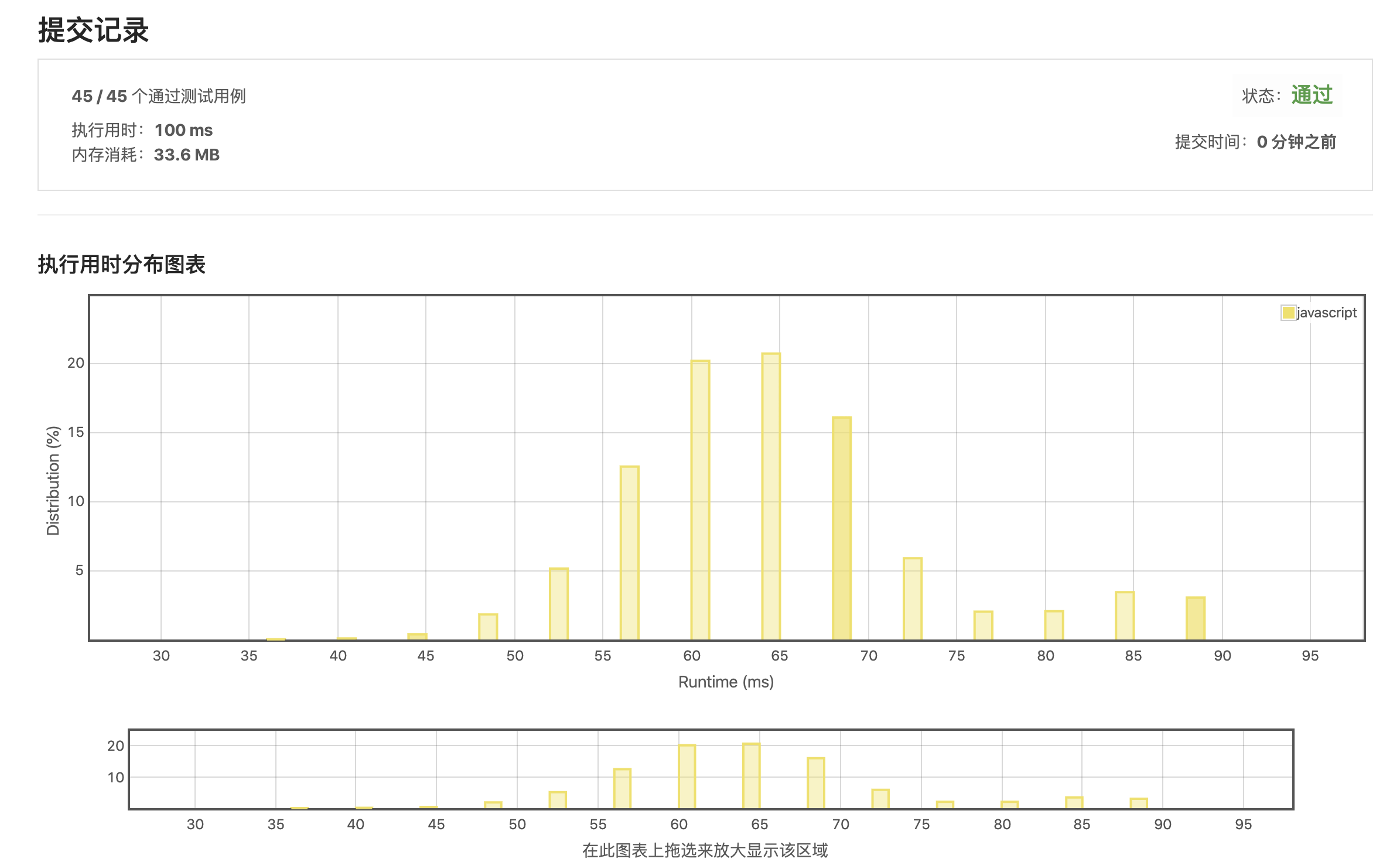
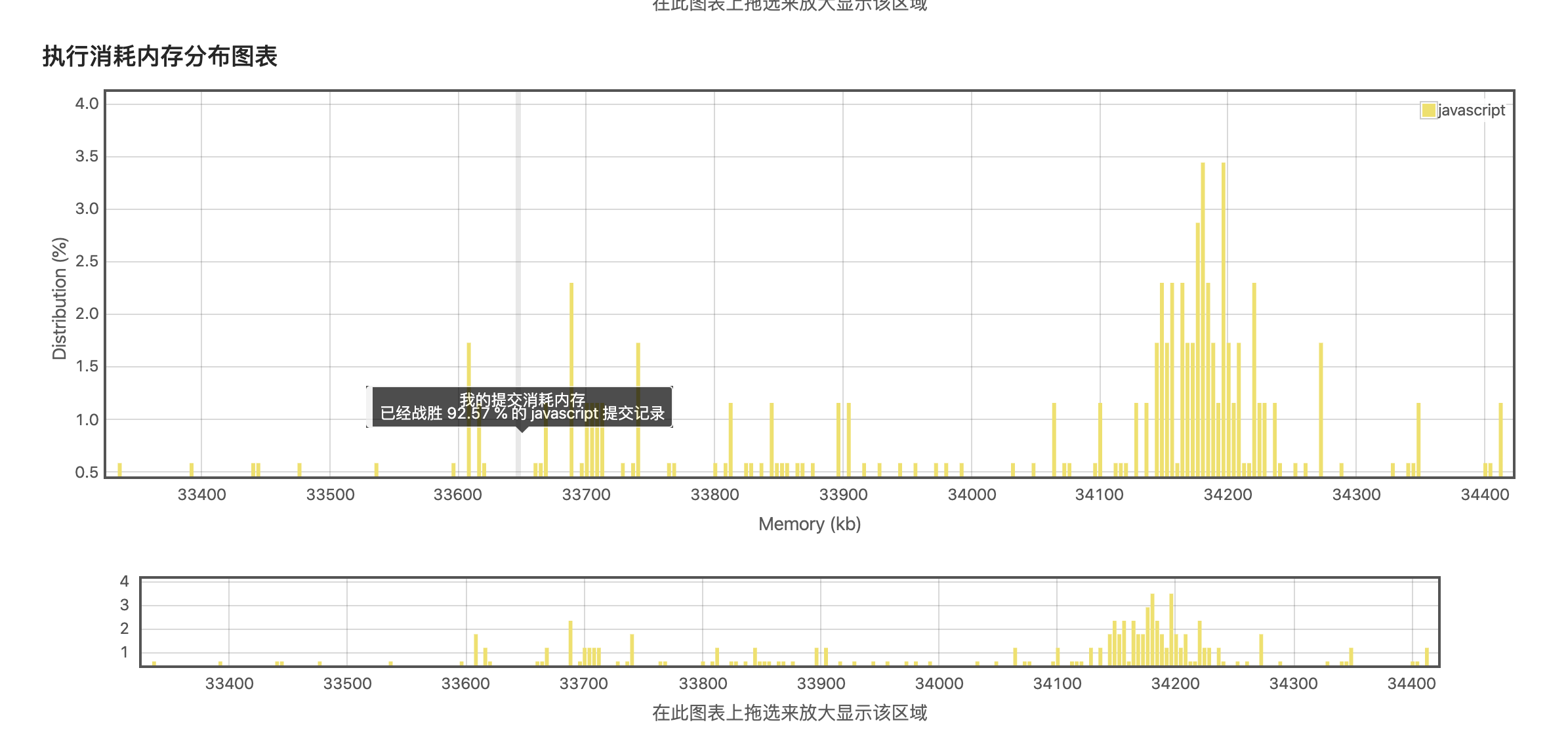
递归算法，好处就是逻辑简单，坏处就是消耗内存，容易造成栈溢出！一笔带过！
最近学习二叉树，发现递归用的很多，而且发现其中的递归的用法很接近栈层面的理解了！不同于在前端层面那种简单的数据嵌套的时候的处理了。
当初，学二叉树没有想出如何插入，遍历的方法。根源是卡在对left节点的操作入栈到了下一层的函数了，但是当前的right节点也需要处理啊，当前的right还没处理了！想想真的是惭愧！说真的，对递归的理解一直都是模棱两可，也就是业务层面处理一下嵌套结构的数据了！

中午，吃饭的时候，看了一下极客的算法视频，专门看了一下递归的。

这位老师其实很牛！讲的都是痛点！所以，我初步总结并树立一个良好的递归观念吧！

递归的认知

我认为，因为有重复性的操作是产生递归的根本原因！
抽离出重复性操作才是重中之重！
暴力递归，重于现象，就是傻递归！不动脑子型的！偏向于演绎法！
抽象出符号递归，重于内部关系，就是真递归！偏向于归纳法！
要会归纳出内部的实质关系，找到抽象递归！递归的问题就会转化，从而效率很高了！

而我总是喜欢演绎法，暴力递归，弄得效率相当地低。需要改进！

题目

吃苹果问题

这个问题最初接触是前一个月左右吧！当初一个前端的朋友，出题：
32个苹果，一个人吃，每次只能吃1个或者2个，一共多少种吃法吃完？？我没记错的话，就这个意思了！
**
当初我还记得我的暴力演绎法，，，，

当初我的思路：

  1. let arr = [[1], [2]], sums = [1, 2];
  2. const x = num => {
  3.     const copy = [];
  4.     sums.map(
  5.         (sum, index) => {
  6.             if (sum) {
  7.                 const item = [...arr[index]];
  8.                 if (sum + 1 <= num) {
  9.                     arr[index].push(1);
  10.                     sums[index] += 1;
  11.                     if (sums[index] === num) {
  12.                         sums[index] = null;
  13.                     }
  14.                 }
  15.                 if (sum + 2 <= num) {
  16.                     item.push(2);
  17.                     copy.push(item);
  18.                     sums.push(sum + 2 === num ? null : sum + 2);
  19.                 }
  20.             }
  21.         }
  22.     );
  23.     // console.log(arr,sums,copy);
  24.     arr = arr.concat(copy);
  25. };
  27. const eat = num => {
  28.     while (sums.filter(val => val).length) {
  29.         x(num);
  30.     }
  31. };
  33. eat(30);
  34. console.log(arr.length);
  35. //这是我当初的基本思路，代码写的可能没现在这版如此的清晰。
  36. //当初，我执着于求出组合的具体内容，根本就不限于题目的结果，一共有多少种！
  37. // 回归到题目，我可以再优化的：
  38. {
  39.     let sums = [1, 2];
  41.     const y = num => {
  42.         const copy = [];
  43.         sums.map(
  44.             (sum, i) => {
  45.                 if (sum === null) return;
  46.                 if (sum === num) return sums[i] = null;
  47.                 if (sum + 1 <= num) {
  48.                     sums[i] += 1;
  49.                 }
  50.                 if (sum + 2 <= num) {
  51.                     copy.push(sum + 2);
  52.                 }
  53.             }
  54.         );
  55.         sums = sums.concat(copy);
  56.     };
  58.     const eat1 = num => {
  59.         while (sums.filter(val => val).length) {
  60.             y(num);
  61.         }
  62.         return sums.length
  63.     };
  64.     console.log(eat1(30));
  65. }
  66. 都是演绎法，说句实话，我从不觉得这个思路错过！

当初，这个前端朋友弄得我很苦恼，毕竟他弄得我以为我思路错了！当初我相当不理解了，甚至有些郁闷，毕竟那哥们有些很那个，他不看你代码，不思考，也不听你解释，就是说你这想法错了！他喜欢舔其他他认为牛皮的人，嗯，对我来说算是挺受打击的。
不过我从不觉得自己错了：毕竟这是硬解，暴力演绎的，如果这都错了，我是无话可说了！

爬梯子问题

然后有意思事来了，我今天正好，看了一下递归的两个视频，看到那个爬梯子的题目，当时我就联想到他出的那个吃苹果的题了，一个思路的！然后，我也不看老师的讲解，准备再如今的角度去考虑，如何爬梯子：

给定n个阶梯，人上阶梯，一步可以上1个，或者两个，问多少种走法？？
**
这道题直接让我想起了吃苹果的题了！然后我就立马直接开始硬推演绎法了，当时我也是木有看老师如何做题的思路的。
于是，自己原本想用递归实现暴力演绎法，结果错了，，，想想挺尴尬的，还专门给那个前端朋友发了，当然，他还是直接给我说你这不对，我反正是不清楚他有木有看思路，还是直接知道结果了。不管他。

错误的暴力演绎法

  1. //错误的思路：
  2. { 
  3.     const storage = {count:0}
  4.     const x = num =>{
  5.         if (num === 0) return ;
  6.         if (num - 1 >= 0 ){
  7.             storage.count += 1   //错在计数的这里的逻辑！要根据上面的吃苹果的增加
  8.             x(num - 1)
  9.         }
  10.         if (num - 2 >= 0 ){
  11.             storage.count += 1   //错在计数的这里的逻辑！
  12.             x(num - 2)
  13.         }
  14.     }
  15.     x(2)
  16.     console.log(storage.count);
  17. }
  19. 本来，这个演绎的思路其实很像二叉树的，当然不是搜索树：
  20.       1
  21.     2     1
  22.  1    2 1   2
  23. **************
  24.    但是还是有个限制，就是一个路径的节点的和小于num！跟路径挂钩，就可以明白上面的计数哪里错了吧！
  25. 真正的纯暴力演绎法，还是要看吃苹果的那个方法！

修改：

  1.          const storage = {count:1}  
  2.     let counts = [1,2]
  3.     const x = (num,lastChange) =>{
  4.         if (num - 1 >= 0 ){
  5.             // 这里不加1，所以走第一步的时候是1的情况，少了，我把初始的count值设为1，为底数。
  6.             x(num - 1,1)
  7.         }
  8.         if (num - 2 >= 0 ){
  9.             storage.count += 1   //因为像极了二叉树的链路，其实每个节点都可以分出两条路径，
  10.           //但是其中总有一条已经计算到count了
  11.             x(num - 2,2)
  12.         }
  13.     }
  14.     x(10)
  15.     console.log(storage.count);

测试

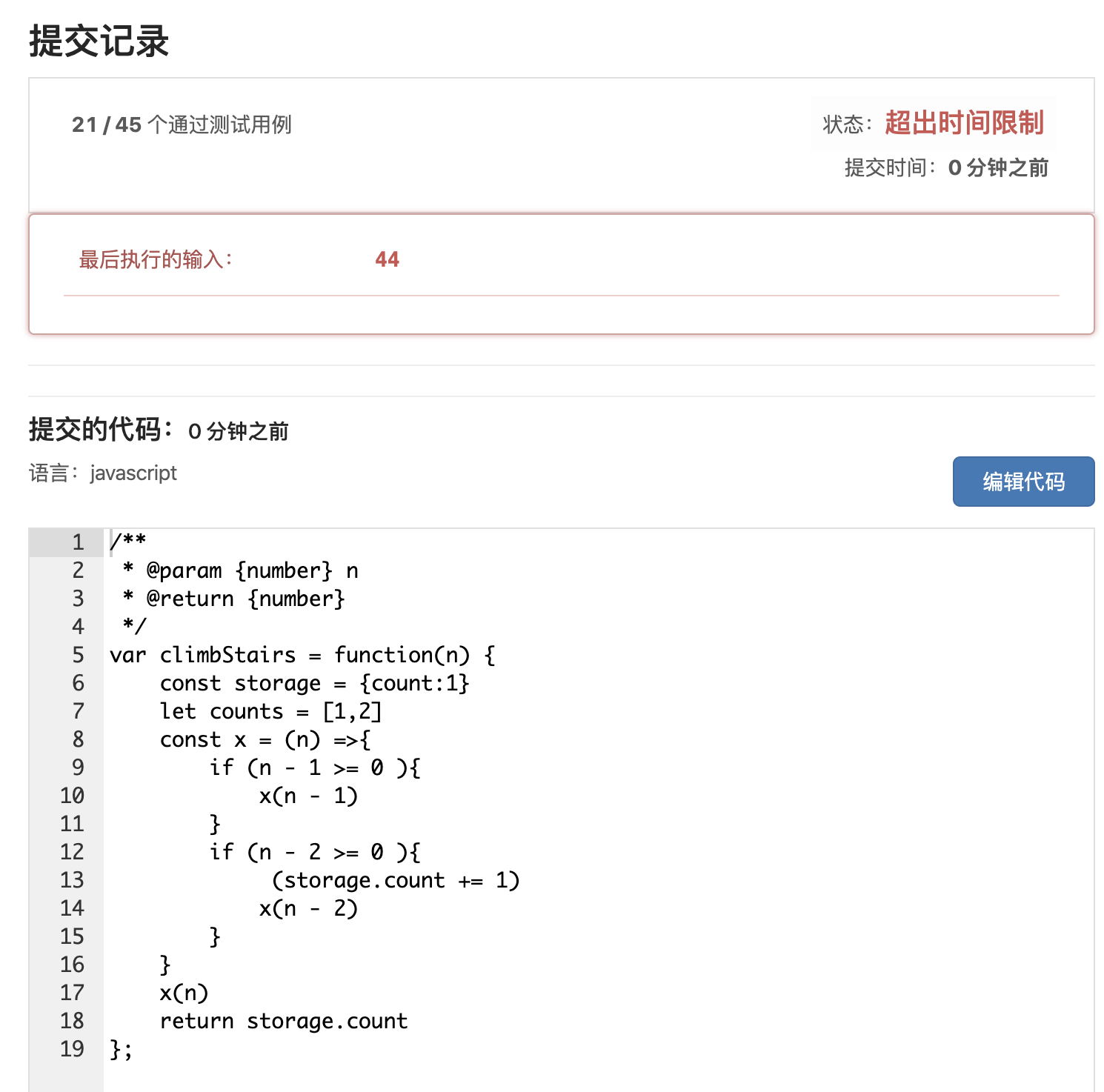
截屏2020-04-07 下午7.18.10.png

效率太低，导致超时了！这就是暴力递归，而且是演绎法的问题所在！
同理，其实吃苹果的那个代码就不再跑了。单个用例小于30多的，抽测几个都是对的。

正确的抽象思路

一般的抽象套路：穷举法

  1.  n =1 :
  2.  1         1
  3. n=2 :
  4. 1,1; 2。   2
  5. n =3 :
  6. 1,1,1; 1,2; 2,1。 3
  7. n= 4 :
  8. 1111;  121;  112; 22; 211;   5    //数学归纳法，就要猜了，，，会不会是 f(n)=f(n-1)+f(n-2)?
  9. n=5:
  10. 11111;1211;1121;221;2111;1112;122;212;  8  //还真是！！

开始抽象：

人走到第n级时，总是要先走到第n-1级，或是n-2级。这就是根本的抽象原理！
人走到第n-1级的情况跟人走到第n-2级的情况有木有冲突？木有！因为最后那一步迈出去的对应为1/2。
互斥，互补！这是最根本的！

转化问题

  1. 求的是f(n) = f(n-1) + f(n-2) 如此的多项式关系了！
  2.         const x = n => {
  3.         if (n === 1) return 1;
  4.         if (n === 2) return 2;
  5.         if (n >= 3) {
  6.             let last1=x(1), last2=x(2), i = 3;
  7.             while (i <= n - 1) {
  8.                 i%2 !== 0 ? last1 += last2 :
  9.                     last2 += last1
  10.                 i++
  11.             }
  12.             return last2 + last1;
  13.         }
  14.     };

截屏2020-04-07 下午10.13.41.png
截屏2020-04-07 下午10.13.55.png

内存少，但是时效太差了！我觉得好奇怪啊哈哈！因为我也看了一下其他的人的代码思路，觉得差不多啊！我就想哪里的问题？？

我突然看到我用的const,let了，，，我心里有些激灵了，立马试了试：

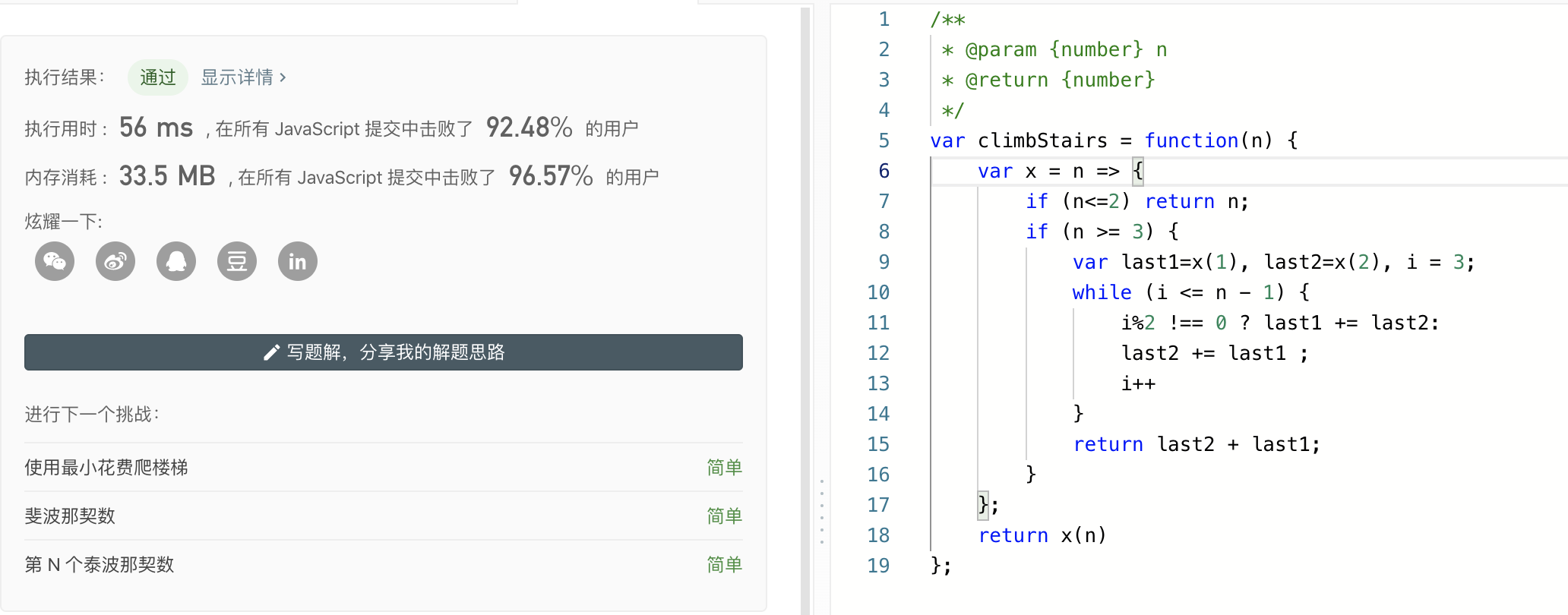
截屏2020-04-07 下午10.19.50.png
啥都不说了！！

总结

只要有重复操作的步骤，就尽可能地去抽象重复步骤，找到重复步骤跟下一次重复步骤之间的关系！
实在找不出来，就先穷举法，然后用数学归纳法去归纳，由一般到n，就找到重复步骤的抽象了！
关键结论，就是抽象出来的重复步骤之间的关系！
因为递归性能差，所以最好用尾递归，相当于迭代的意思了！

练习题

有效括号问题

截屏2020-04-07 下午10.32.51.png

这道题，要很好地理解题目要做什么？如何做到？
3对括号，就是3个左括号，三个右括号！
先不复杂化，先做出，三个左括号和三个右括号的左右的排列情况，然后再考虑其中哪个不合格！
第二个点就是，如何筛选不合规矩的排列：右括号不能大于左括号数！

尾递归

  1. //括号问题 https://leetcode-cn.com/problems/generate-parentheses/
  2. {
  3.     let arr = [
  4.         {
  5.             val: "(", left: 1, right: 0, ok: false
  6.         }
  7.     ], res = [];
  8.     const x = (n) => {
  9.         while (arr.length) {
  10.             const arr1 = [];
  11.             arr.map(
  12.                 ({val, left, right, ok}, i) => {
  13.                     if (ok) return;
  14.                     if (right < n) {   //这里有坑！第一顺序不可颠倒，否则提前拷贝；2，如果left满了，就不需要复制添加了
  15.                         if (left < n) {
  16.                             if (left < right) {
  17.                                 return arr[i].ok = null;
  18.                             };
  19.                             const copy = {val, left, right, ok};
  20.                             copy.val += ")";
  21.                             copy.right += 1;
  22.                             if (right + 1 === n && left === n) {
  23.                                 copy.ok = true;
  24.                                 res.push(copy.val);
  25.                             } else {
  26.                                 arr1.push(copy);
  27.                             }
  28.                         } else {
  29.                             arr[i].val += ")";
  30.                             arr[i].right += 1;
  31.                             if (right + 1 === n && left === n) {
  32.                                 arr[i].ok = true;
  33.                                 res.push(val + ")");
  34.                             }
  35.                         }
  36.                     }
  37.                     if (left < n) {
  38.                         if (right > left) {
  39.                             arr[i].ok = null;
  40.                         } else {
  41.                             arr[i].val += "(";
  42.                             arr[i].left += 1;
  43.                         }
  44.                     }
  45.                 }
  46.             );
  47.             arr = arr.concat(arr1).filter(val => val.ok !== null && !val.ok);
  48.         }
  49.     };
  50.     x(n);
  51.     return res;
  52. }

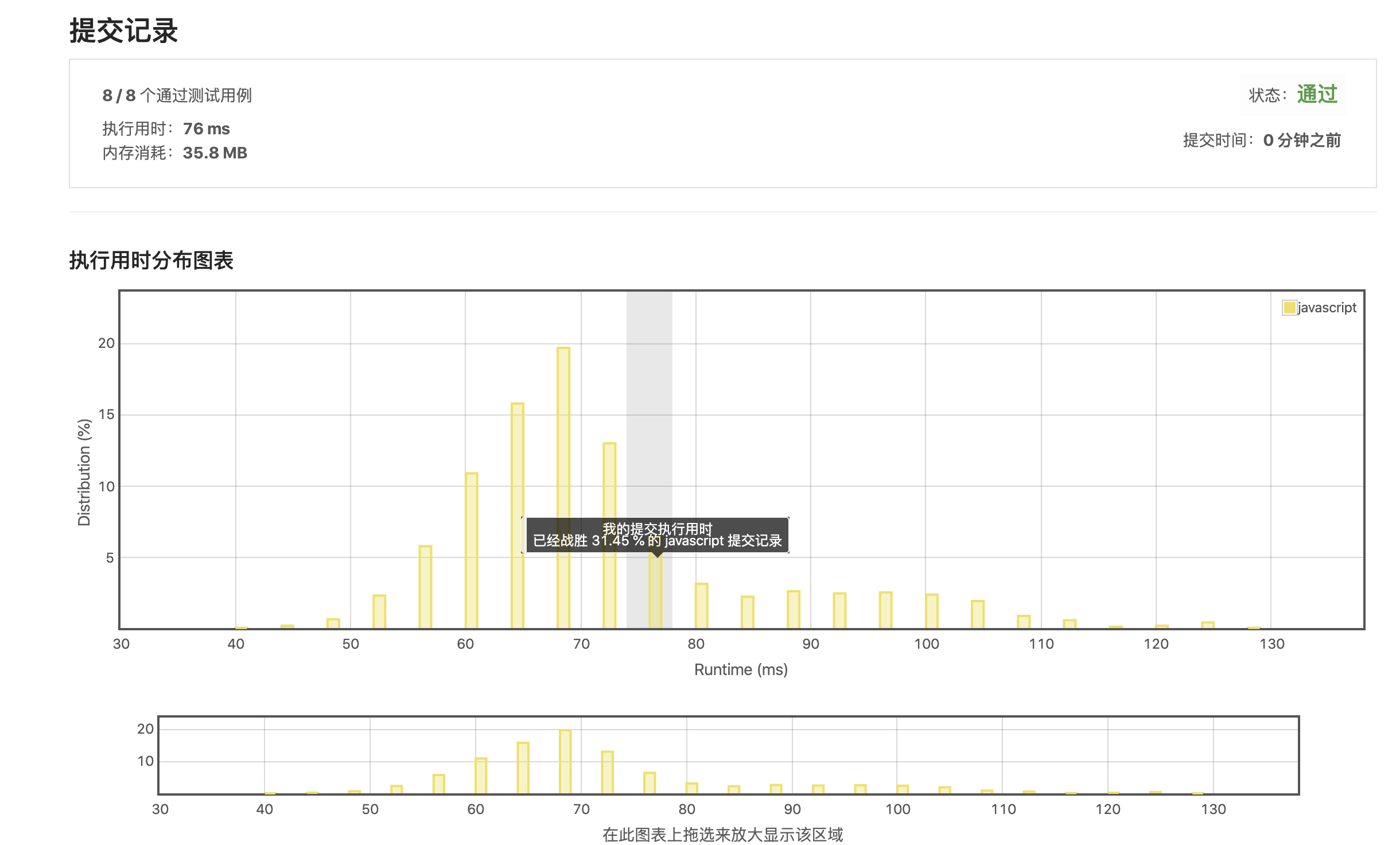
截屏2020-04-08 上午12.53.23.png
截屏2020-04-08 上午12.53.37.png
时效性还是太差了！！我想了想应该跟强制性地递归有关系的！

纯控制性递归思路

  1. {
  2.     var res = [];
  3.     var x = ( n, s,left,right) => {
  4.         if (left === n && right === n) return res.push(s);
  5.         right<left && x(n,s+')',left,right+1);
  6.         left < n &&left>= right && x(n,s+'(',left+1,right);
  7.     };
  9.     x(3,'',0,0)
  10.     console.log(res);
  11. }

不知道为什么，我总是喜欢尾递归，，，还不如递归来得快！涨涨记性！

递归求乘

截屏2020-04-08 下午1.57.31.png

  1. var multiply = function(A, B) {
  2.         const min = A > B ? B : A;
  3.         const max = A > B ? A : B;
  4.         let i = 1, res = max;
  5.         if (i === min) return res;
  6.         const y = (i, res) => {
  7.             if (i === min) return res;
  8.             if (i + i <= min) {
  9.                 res += res;
  10.                 i += i;
  11.             } else {        //只有两种分法，会让数据大的时候吃亏的。所以我尝试了优化了一个中庸版的
  12.                 res += max;
  13.                 i += 1;
  14.             }
  15.             return y(i, res);
  16.         };
  17.         return y(1, max);
  18. };
  21.  const x = (a, b,) => {
  22.         const min = a > b ? b : a;
  23.         const max = a > b ? a : b;
  24.         let i = 1, res = max,max100,test,add;
  25.         if (min === 0) return 0;
  26.         if (i === min) return res;
  27.         if(min>1000){
  28.             if(min<10000){
  29.                 test = i => i> 100 && i+100<=min
  30.                 max100 =+( max+  '00')
  31.                 add = 100
  32.             }else{
  33.                 test = i => i>1000 && i+1000<=min
  34.                 max100 = +( max+  '000')
  35.                 add = 1000
  36.             }
  37.         }
  38.         const y = (i, res) => {
  39.             if (i === min) return res;
  40.             if (i + i <= min) {
  41.                 res += res;
  42.                 i += i;
  43.             }
  44.             else if(min>1000 && test(i)){
  45.                 res += max100
  46.                 i += add
  47.             } else {
  48.                 res += max;
  49.                 i += 1;
  50.             }
  51.             return y(i, res);
  52.         };
  54.                 //这里有过测试，每增加一次判断，消耗增加，我为了适应后期大数量级，觉得应该填一个。
  56.         return y(1, max);
  57.     };