基于数组进行实现的,源于数组的插入,删除的性能垃圾,才有了哈希表
优点:
- 快速地插入删除操作,打脸数组。
我这里想起了前几天写的自认为小聪明的排序算法了,,,插入,删除,虽说当时是赋值,取值,但依旧是对n多项进行的操作了。其实取值赋值应该是插入删除的基本实现了,没差了。
- 查找比树还快,,,我暂时没树的概念,盲猜跟关系型数据库构建的主键副键构成的关系一个样子。
- 相比树来说,编码更容易。
嗯!确实是很牛皮,视频里的大牛说了,很伟大!
我之前也努力构思过,除非我建立一个字典,字典的key关联数组的每个下标的值,value为下标的index。如此,不就可以通过key拿到index了,查找就快了。
但是删除,插入,,,确实是!数组的数据结构本身就限制了插入和删除的性能了!
缺点:
- 无序,无法从大到小或从小到大遍历,估计跟下标魔改有关,,,
- 通常情况下,,,难道有不通常??key值唯一。这里埋个雷了。暂定唯一!
数据结构
无法描述,一说就全都露馅了。
基于数组实现的。
对下标值的变换,是关键。通过哈希函数实现的。拿到hashCode。
引子:

案例一:
数组
下标查询,查询快!就是删除慢,员工信息查询慢!
下标需要查员工的下标!
链表**
查询慢,增删快!
如果把员工的名字通过特定的规则转化为index下标。每次通过员工的名字,通过规则函数算出index,那查看多好,,,跟我在上面对于数组的查询的优化一样的逻辑了。
案例二,案例三:
字典的味道,,,
我会用集合,当然之前用对象封装的集合有缺陷的,需要魔改一下!
老师强推数组,链表的逻辑,,,很木得涵养了。强行引出了核心理念,要存入的数据的核心id,根据一个函数算出一个index。把数据存入index。就可以了!
如何转index
字母转下标
如何将字母转成数字?规则?字典如何设计?
字符编码?美国的ascll?欧洲的规范ISOXXX?中文的GBKXXX?还是神Unicode?
毕竟是大一统的规范了。
设计标准字典
我自己设计一下,a-z,从1到27,A-Z,28到54。字典多简单!
实现下标,保证唯一性
然后如何实现下标?
- 累加? 1 + 5 === 2+1+1+2,不行!
- 太小的相互计算会重复!要变大! 254^3 + 1254^2 + 3 => cmd ,这种幂运算基本很难重复了!
但是如此大造成了,生成的数组的长度变大了,浪费内存!!
哈希化

为了不让重复,尽可能地让字母组成的单词到数字的转化计算,用幂运算参与!
幂运算会造成数组的长度太长,浪费内存!
不可能会用累加的,还是要用幂运算。只不过幂运算后的结果,压缩到一个特定的数据范围内!
也就是说,数组的长度需要比目标数据的个数多,多多少?自己定,只要不是太多就好了。
取余操作实现压缩
意图很明显,分数值的范围来压缩映射到对应的范围。幂运算的得出的数值之间差别很大,数值通过取余之后对应各自的映射的范围的下标。可以规定0-199的下标在0-10之间。
这种压缩逻辑很实用,源于幂运算的结果之间的差距在经过压缩后依旧那么随机分布。且差异很大。不同于连续累加的那种紧凑感。
哈希表

冲突

冲突不可避免,源于哈希表本身靠的是压缩的值本身是活的,压缩的取余方法是死的。
只能出个fix的方案了。
链地址法
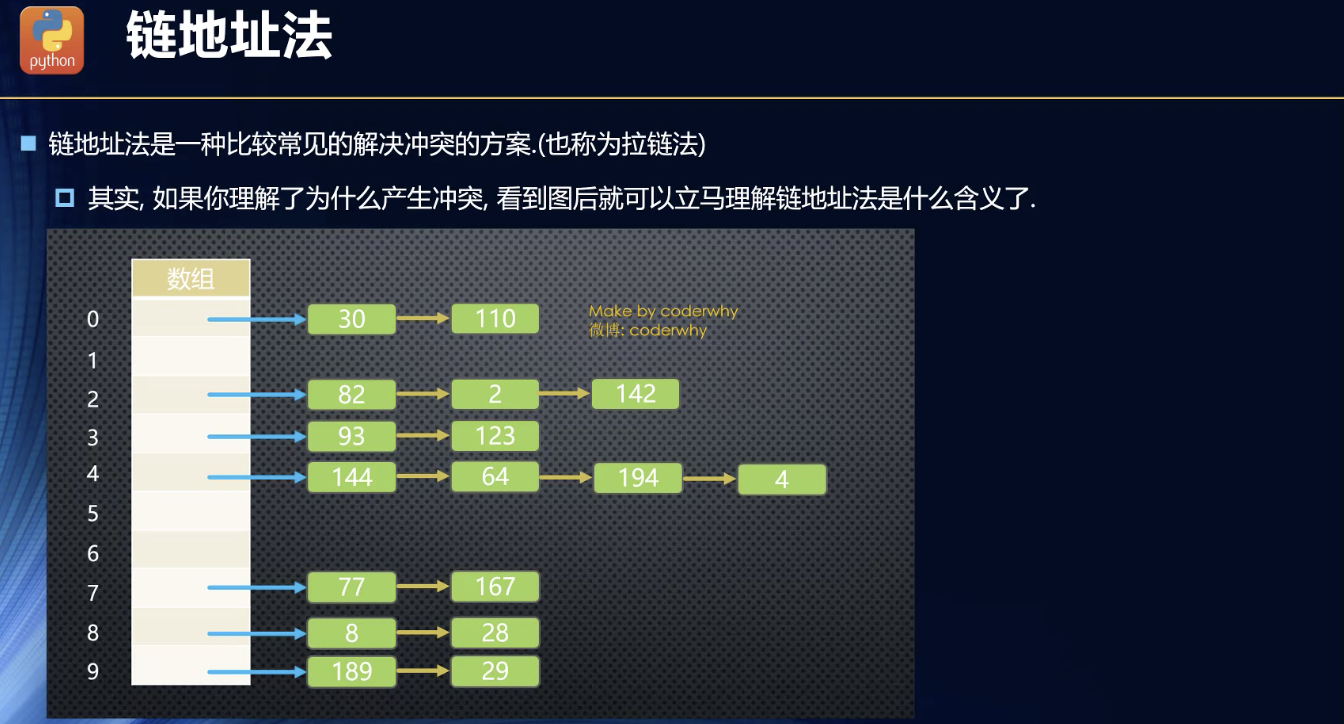

相当于一对多的关系了。其实就是关系型数据库中的主键的表跟副键做主键的表的关系。
老师说的,,,基本上冲突很少。这个冲突频不频繁就需要建模了,但是我觉得没必要,否则就是那个幂运算那里出问题了。
冲突的那些数据共用一个下标,然后自己由于,,,嗯!默认冲突很少,所以,就采用数组或者链表的形式存储成一个整体。
至于用数组还是链表,,,我在想为啥不用哈希?确实是没必要,毕竟默认冲突很少,哈希的面向数据量还是很大的。
开放地址法
核心——寻找空白单元

遇到重复的,就寻找空白单元,填入数据!但是如何寻找?这很关键!因为涉及到如何取值的操作!
有三种方法。。。
线性探测

思路:
从定位的index下标开始,递增傻瓜式查找空白单元!
疑惑——这很可能会占据原本其他的还未填入的数据的位置,我心里觉得别扭!相当于多出来了不必要的查找!
注意点:
就是删除操作了。因为查找和取值相当于链式因果了。如果中间的一个节点被删掉了。查找的规则是遇到空位就停了。后面的节点就拿不到了,所以规定删除的节点不能为null。

缺点:
聚集,就是连续递增的添加情况。对后续的重复的数据找空位就要一个个地过太多的实体位了。而且聚集会越来越大。
二次探测-针对线性探测的聚集问题

因为探测的时候,每次都是递增1位进行探测的。太慢了,那就每次探测递增的位子大点。
这可以解决连续递增或递减的插入了。
但是不能解决连续插入同一个下标的情况,连续插入同一个下标,也会聚集。这种情况有,很少!
如何真的做到,不聚集?
肯定是步长不能一样的!每次插入的步长都不能一样。
再哈希法
根据不同之处,进行再次映射,这次的映射有点放大范围的意思。

效率?选哪种方法
盲猜是链地址法。源于开放地址法背离了数组的index的优点,反而自己增加烦恼!南辕北辙!
至少链地址法,性能比数组好!而,,,开放地址法是把有序的数组复杂成无序的数组了,貌似是这种感觉。
看老师的解析。。。
效率入手点

查找的难度跟总数据项与哈希表长度有关。
效率统计模型测试

它的意思是,靠内存,内存越大,效率越高,不断扩容。那确实是肯定的。
记得说这种开放空位法时,我就觉得怪怪的,把原本的初衷都消耗没了。南辕北辙!
我认为的最理想的状态是——
原本的所有的数据里,不重复下标的先放进去,然后再考虑利用剩余的空位!这样才不会浪费掉那些原本就不重复的数据的下标的高性能。否则,还不如数组高效了!

也无须多解释跟上面的一个道理,虽然相比线性探测,把填装因子的高效范围拉大了很多,但是后期依旧感人,依然是吃内存的大户。毕竟还有一个更加突出的链地址法:

结论:链地址法真香!
回归到实现的初始:哈希函数
哈希函数:
通过特定的value按照字典转化为数字,数字之间通过幂运算逻辑,放大运算结果,为了避免重复。
结果大了,现在想要通过哈希函数把结果压缩,映射到特定的一个小范围的数量区间。
哈希函数要有什么要求,按照什么规则设计?

- 要快!尽可能地运算不复杂!
- 尽可能地算出来的重复的不多,也就是均匀分布。
这两点都是为了性能提出来的。
要尽可能地运算得出值的运算要快
这里我猜的:运算,其实我知道位运算应该会很快的。但是我不确定位运算的重复率高不高了。
老师说的对——乘除运算太消耗性能。
所以,尽可能地加减,乘除尽可能地少!

提取公因式,一层层地提取,从最公共的开始提取公因式,,,
套路了!我觉得我对计算机科学的套路不了解了!
如何均匀分布??
我是真的一点感觉都木有,我还是要思考一下,不能认输!
。。。
算了,对它的套路不熟悉,真的是木得感觉的。
直接拿来主义:

尽可能在用常量时,用质数!
至于为啥??看了老师的示例:
原本有些晕,现在终于明白点了!
错位再循环的感觉!这样避免了死循环,同时可以尽可能地循环到大多数位置。
至于说链地址法中的质数没那么重要,我的感官是源于,因为重复的不多!就算有重复的,也对不重复的无影响。
上面说过我对开发地址法的不友好的原因了。
JAVA的HashMap的介绍:


