树结构——主论二叉搜索树

生活中的树结构

生物树形态

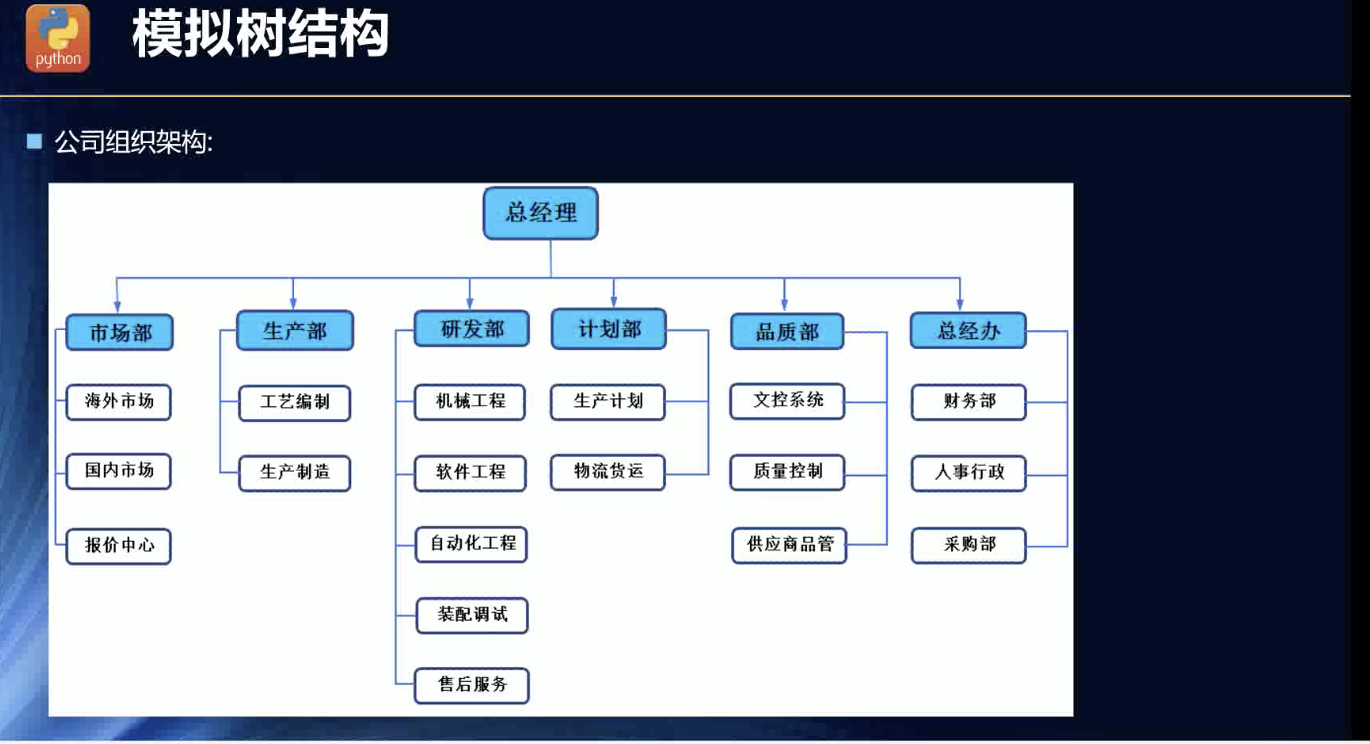
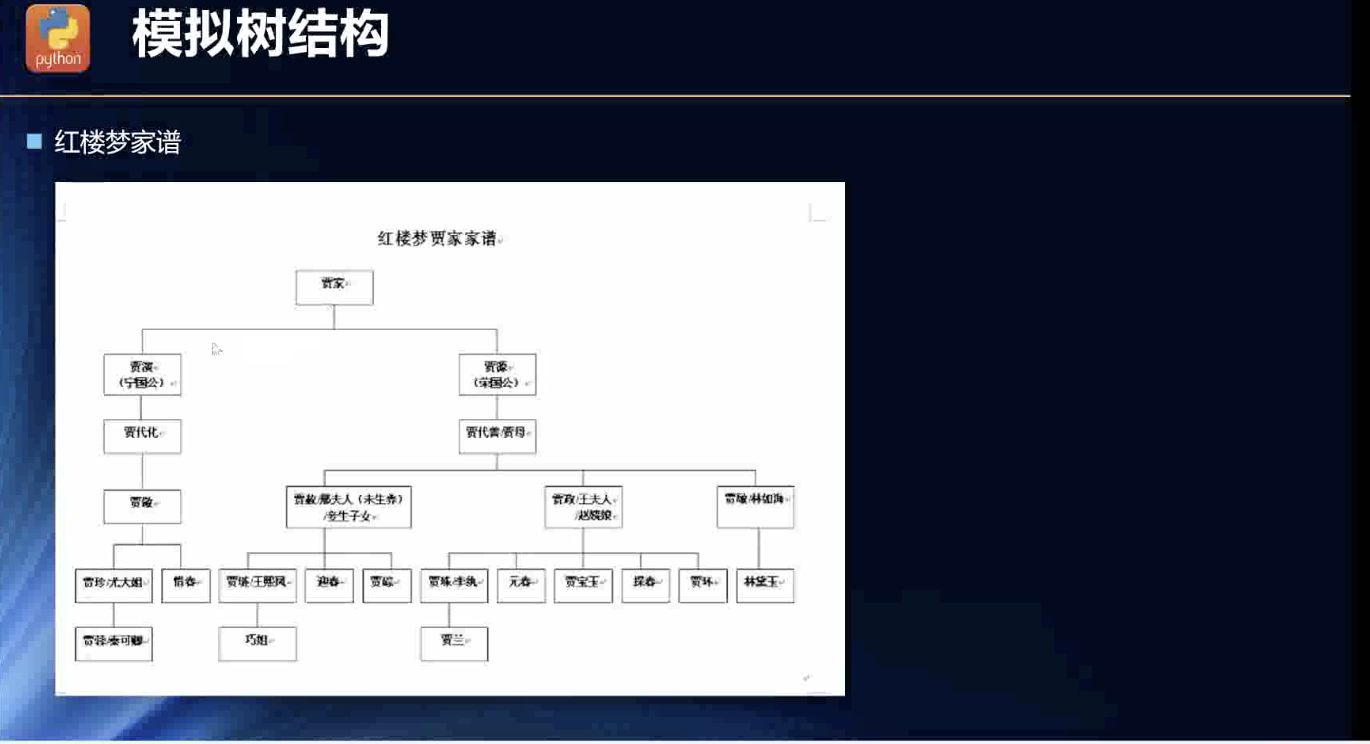
社会文化中的树结构

抽象出来的树结构

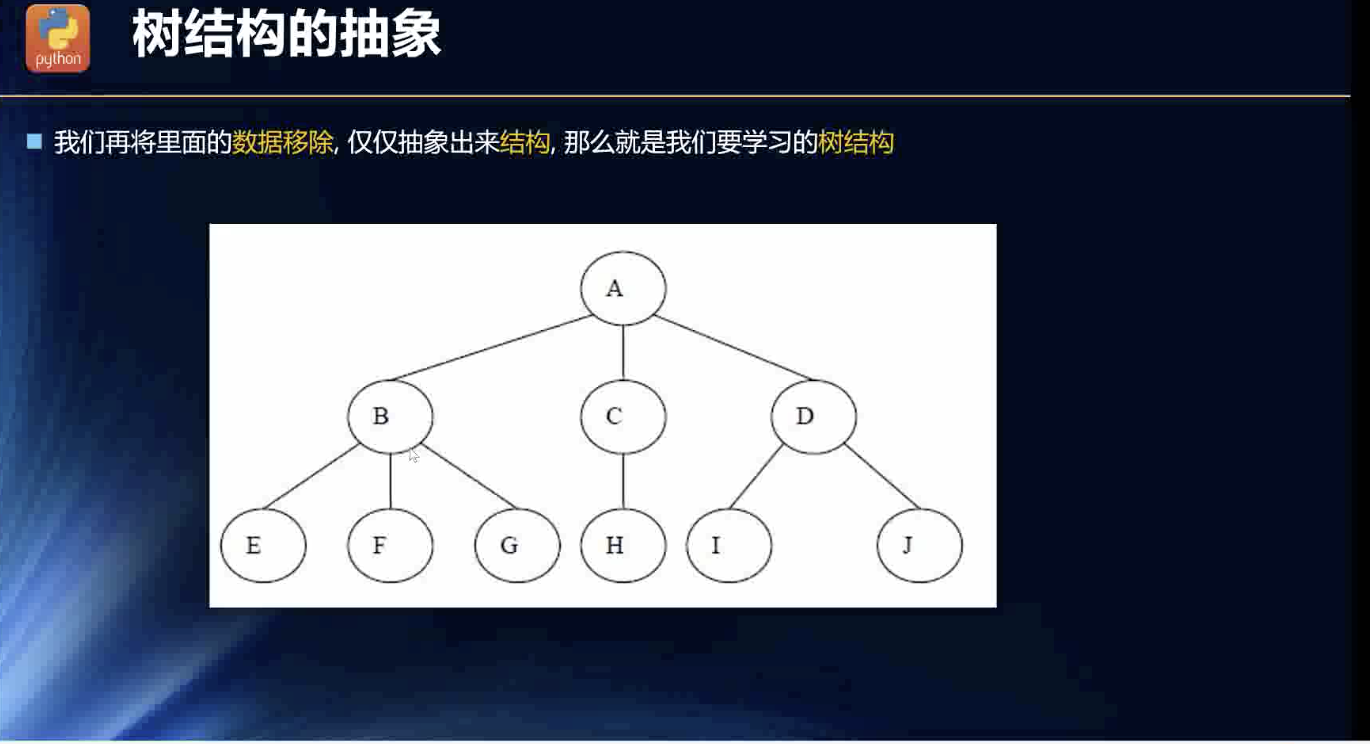
分析：

• 倒立的树。
• 根节点。
• 子节点又可以分成两（逻辑上的两个，是非题的价值参考了）个子节点。

数组链表的优势劣势

数组的优点：用下标读取和赋值很快。
数组缺点：查找，很慢，盲目遍历。除非先排序，再二分查找！删除，插入操作效率低。还有扩容。
链表的优点：随意插入删除，不需要位移所以效率高。查找也是盲目遍历。不考虑扩容问题。
链表的缺点：查找很慢，也没法排序，二分法。

哈希表与树结构的对比

哈希表的优点，查找，插入，删除都很快！
哈希表的缺点，消耗内存。无序的排列。无法快速找出最大值，最小值。

树结构，仿生的结构，层级关系，一对多的关系，等等。

树结构理论

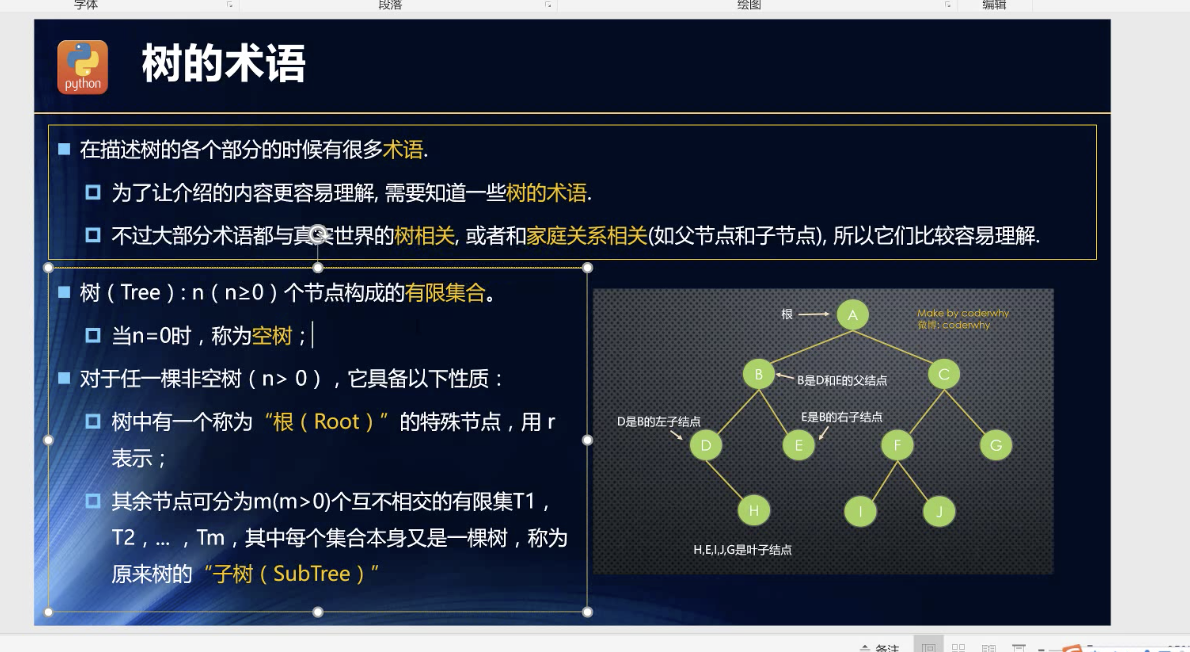
概念 术语

tree ， root , subTree
**

degree

普通表示方式

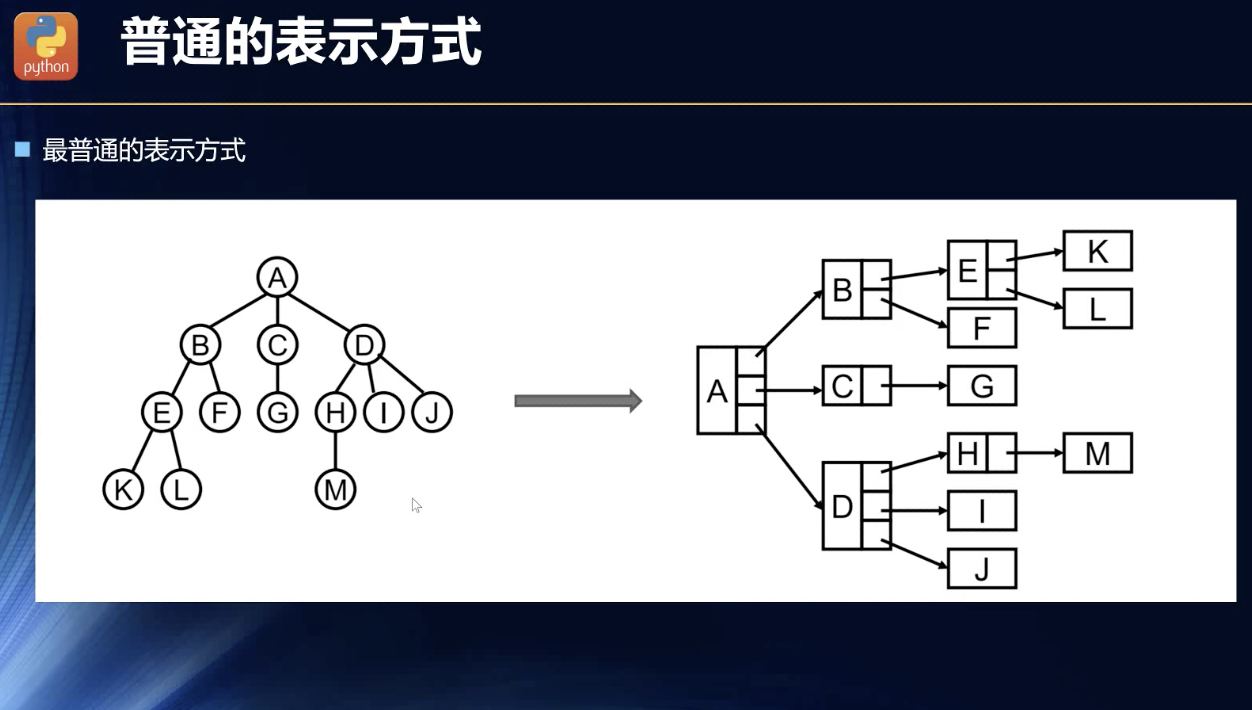
这里很不明白了，感觉很容易构建的，，，

{
  parent:XXX,
  children:[],  //这里老师说很难表示，因为一个，两个，三个，，，left,middle,right。没法表示
  level:XXX,
}

我想了一下，自认为明白了，如果用数组去存储children,那还会高效？其实就是普通的数组加了个外包装而已了！树结构，全都是下标类似的查找，而下标不是数字，而是属性名。

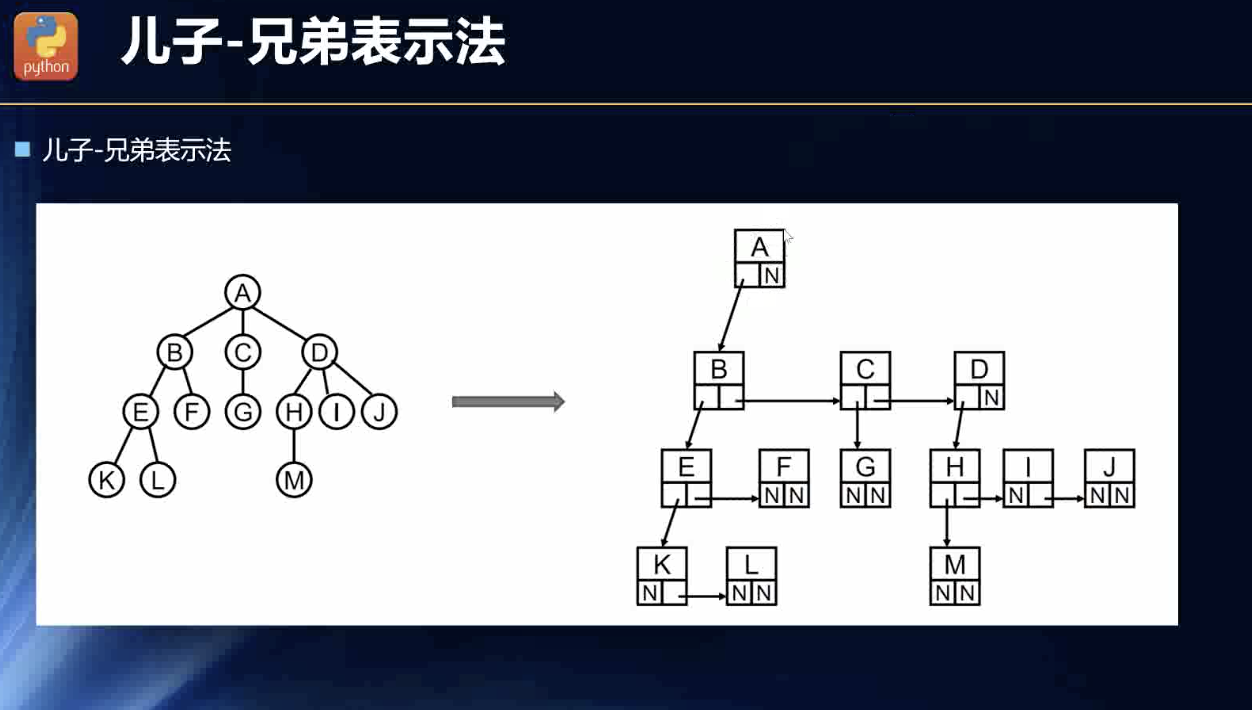
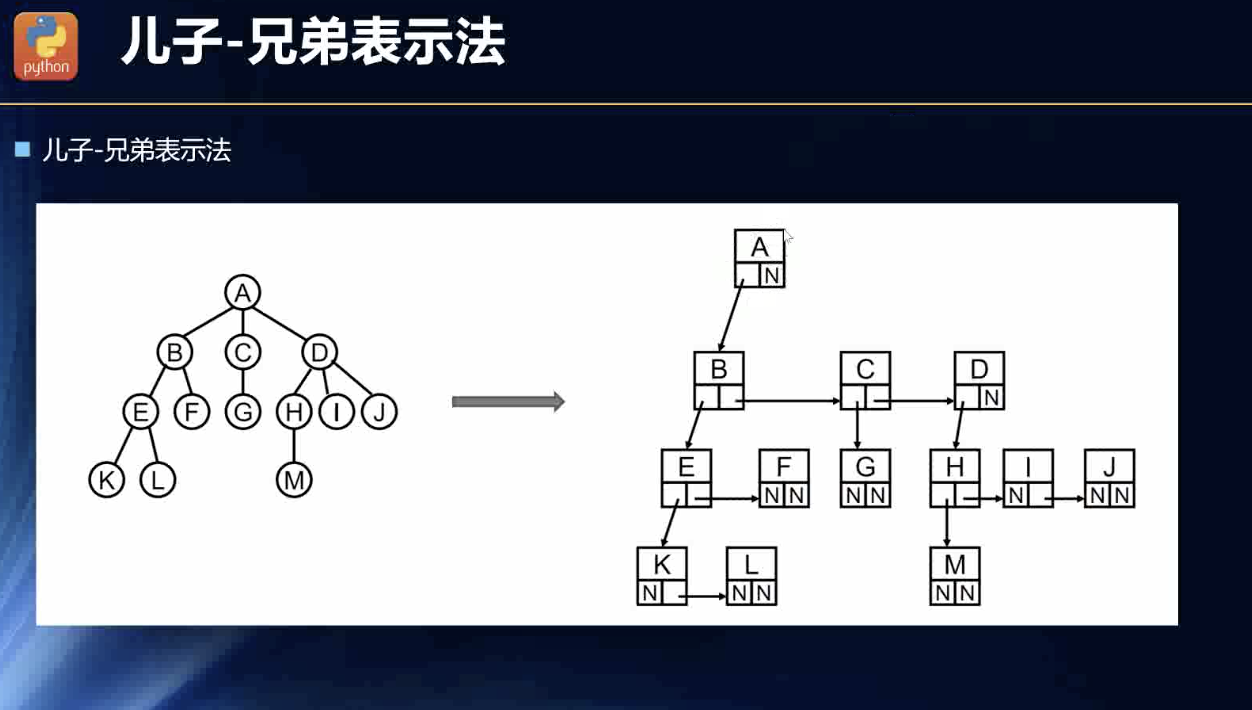
儿子兄弟表示法

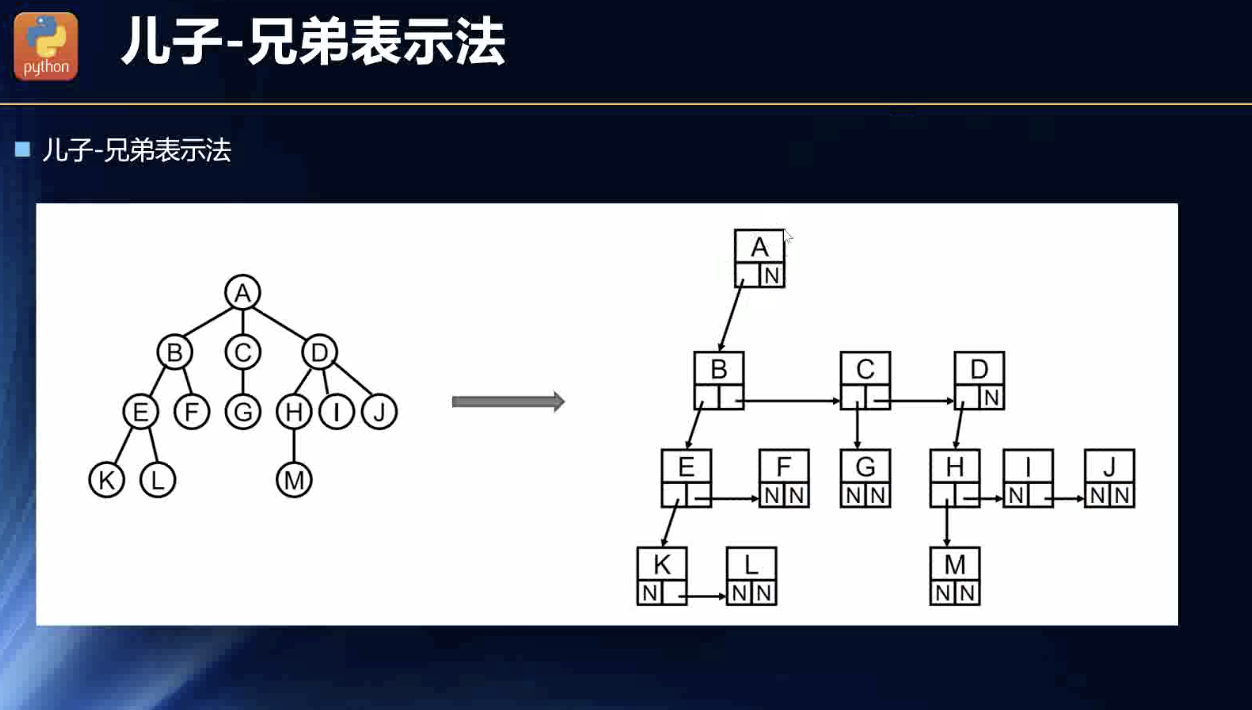
这种数据结构可以链式调用了：

Node {
    data : XX,
    parent:XXX,
      level:XXX,
        sibling: otherNode
}

推出二叉树

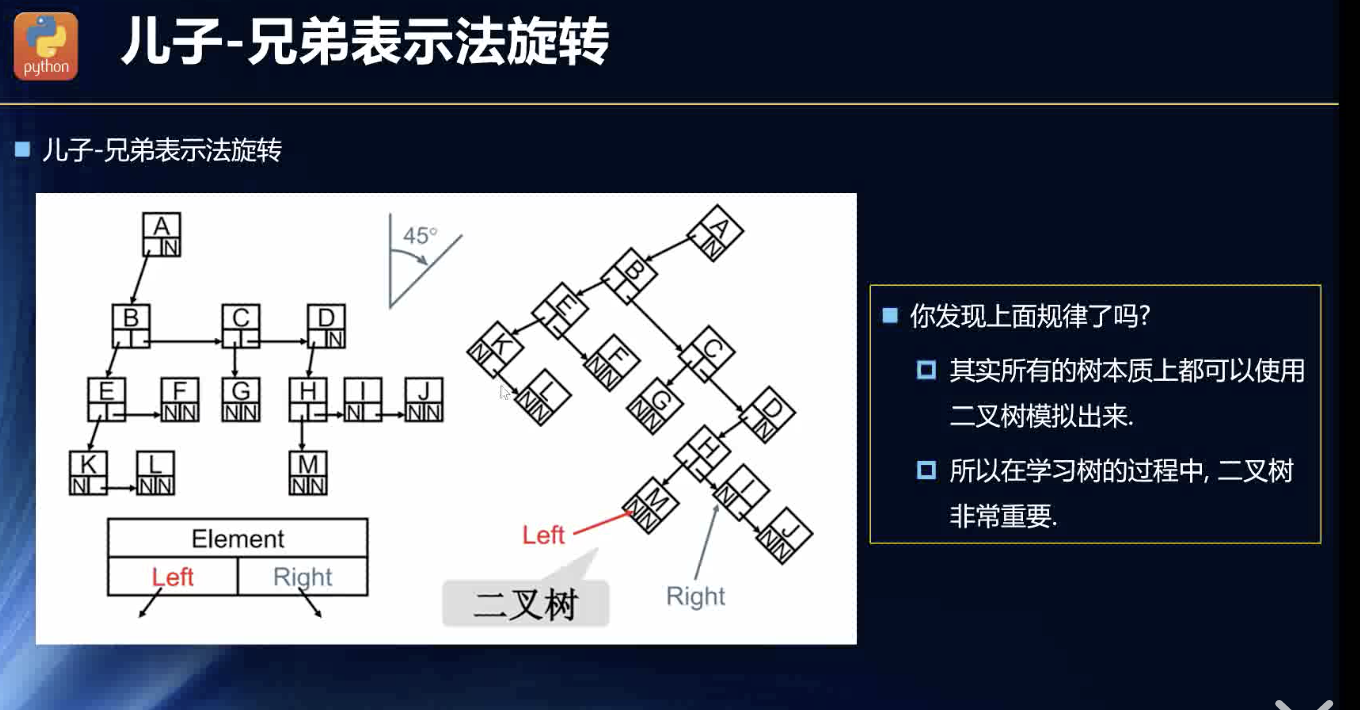
每个节点最多有两个子节点！
我对于这种变换的哲学逻辑其实挺感兴趣的，这是一种逻辑上的集权了。
简单来说就是长兄如父！如果回归到之前的管理层行政职能的树形结果来说，就是总经理跟下一层级的一个职务结合了。比如假如省长又兼职了一个市的市长如此的感官逻辑了。

二叉树概念

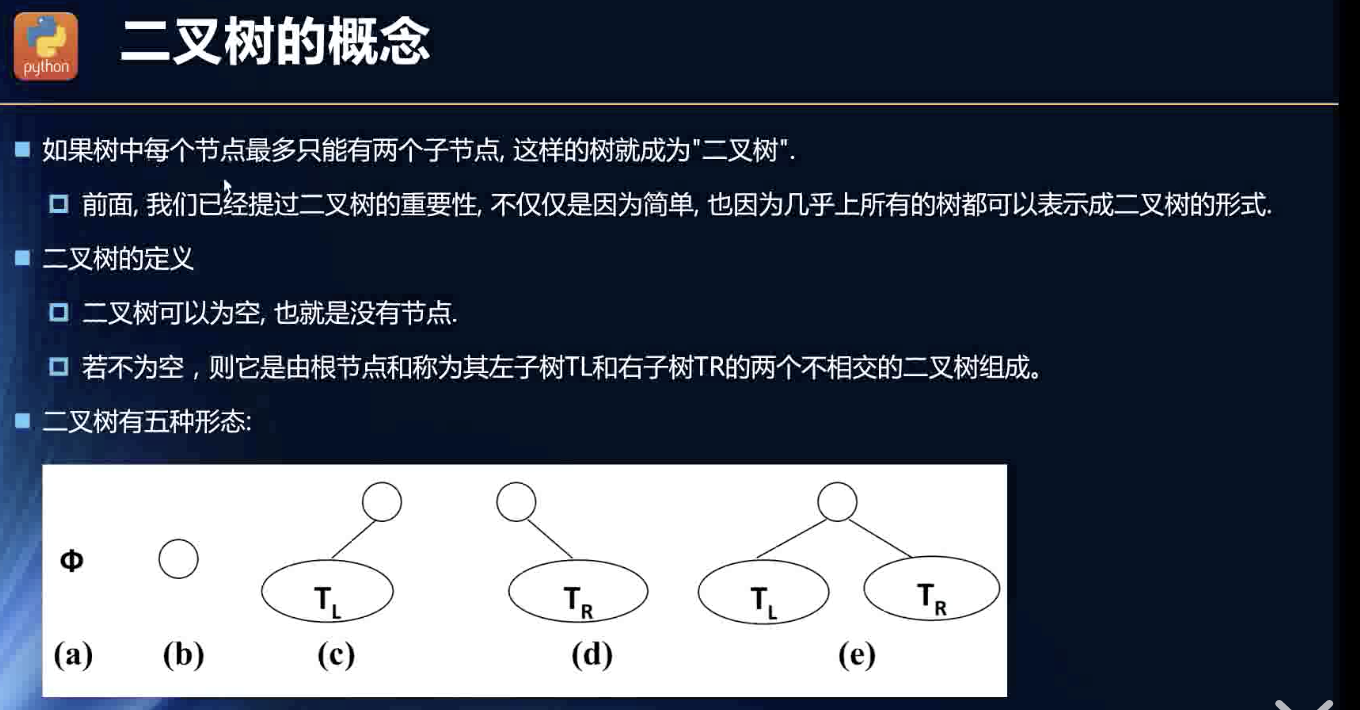
任何树都可以转化为二叉树的形式。所以二叉树很重要！

二叉树特性

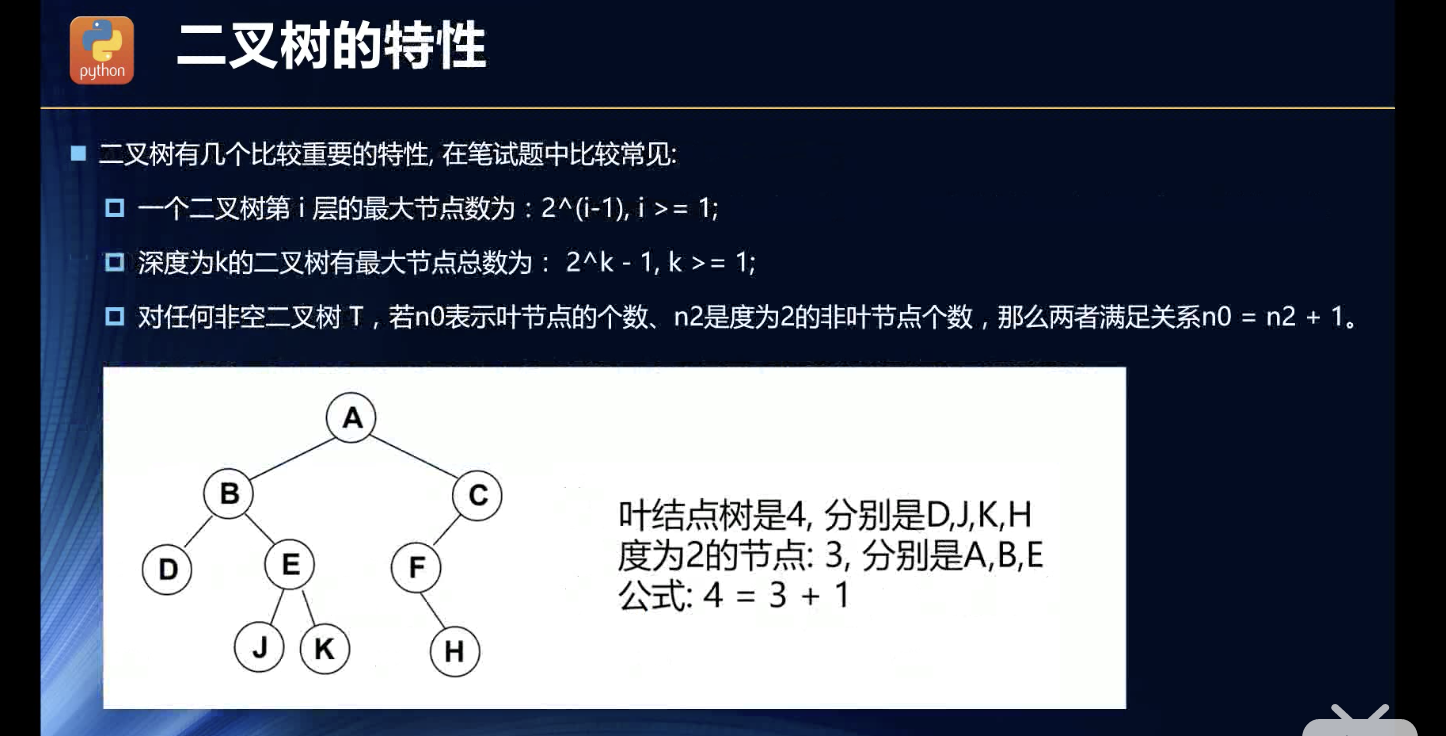
完美二叉树

满的：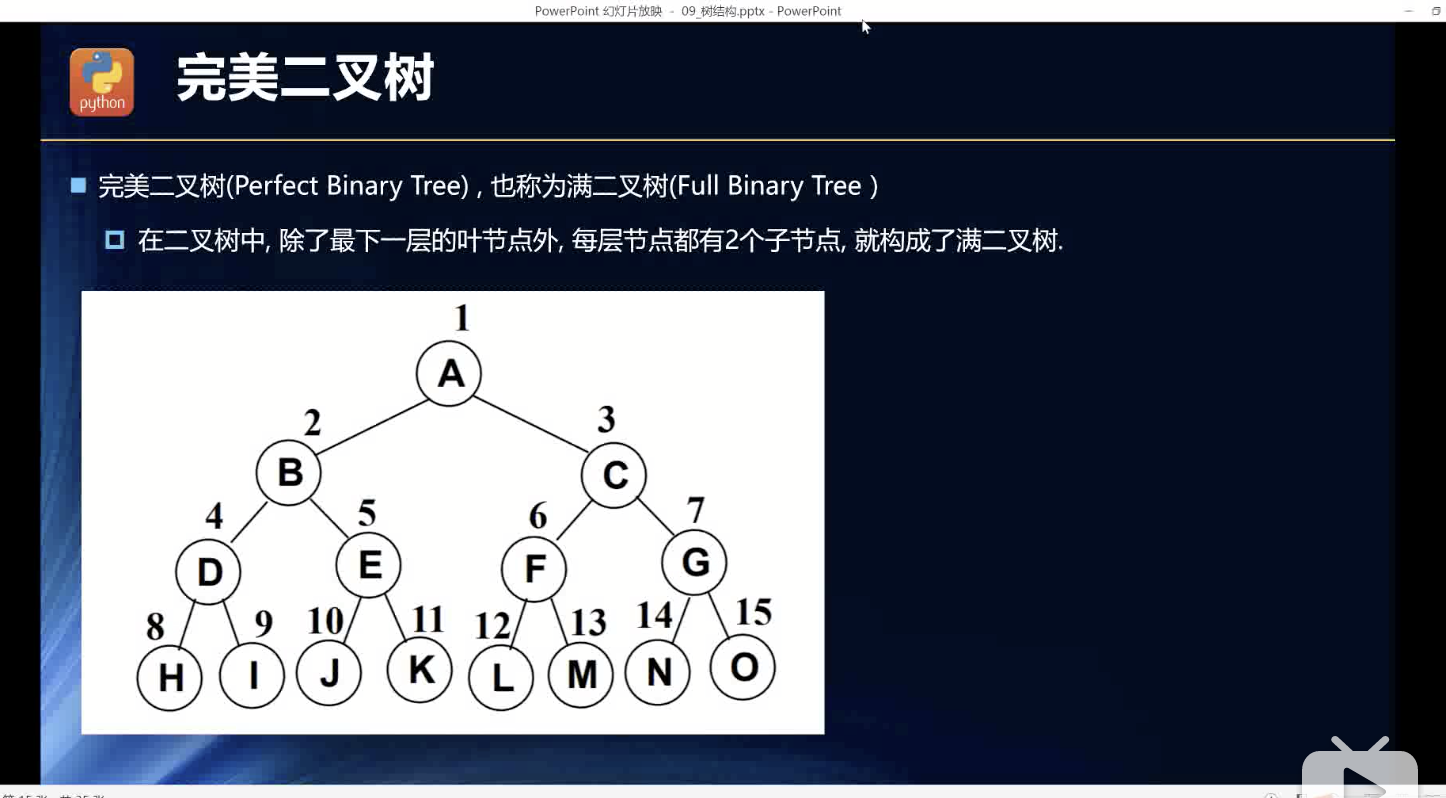

完全二叉树

最后一层：从左到右开始缺失。

二叉树结构

数组表示不行

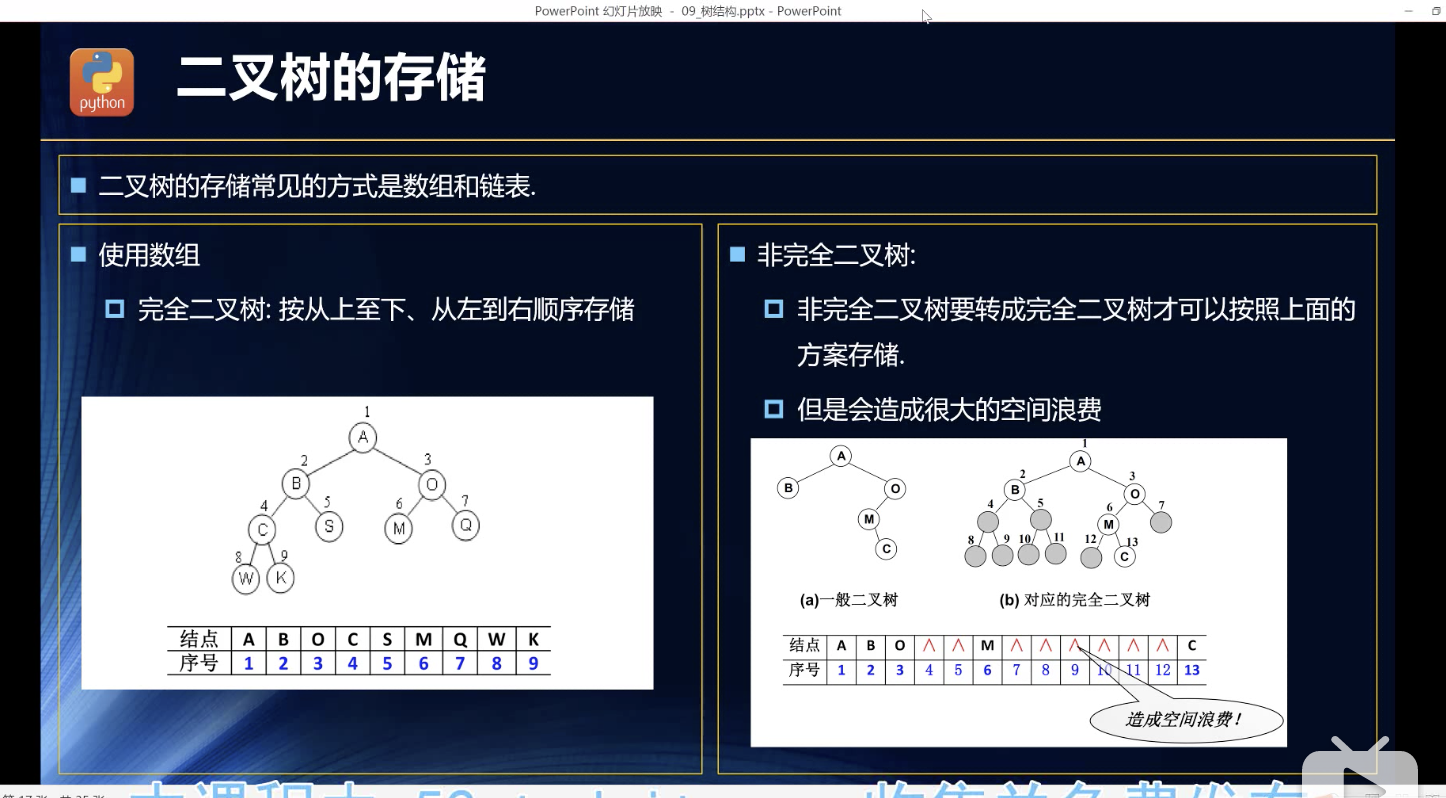
this.leftIndex= this.index * 2 
this.rightIndex = this.index*2+1

很简单，但是非完美二叉树就没办法了。

链表表示

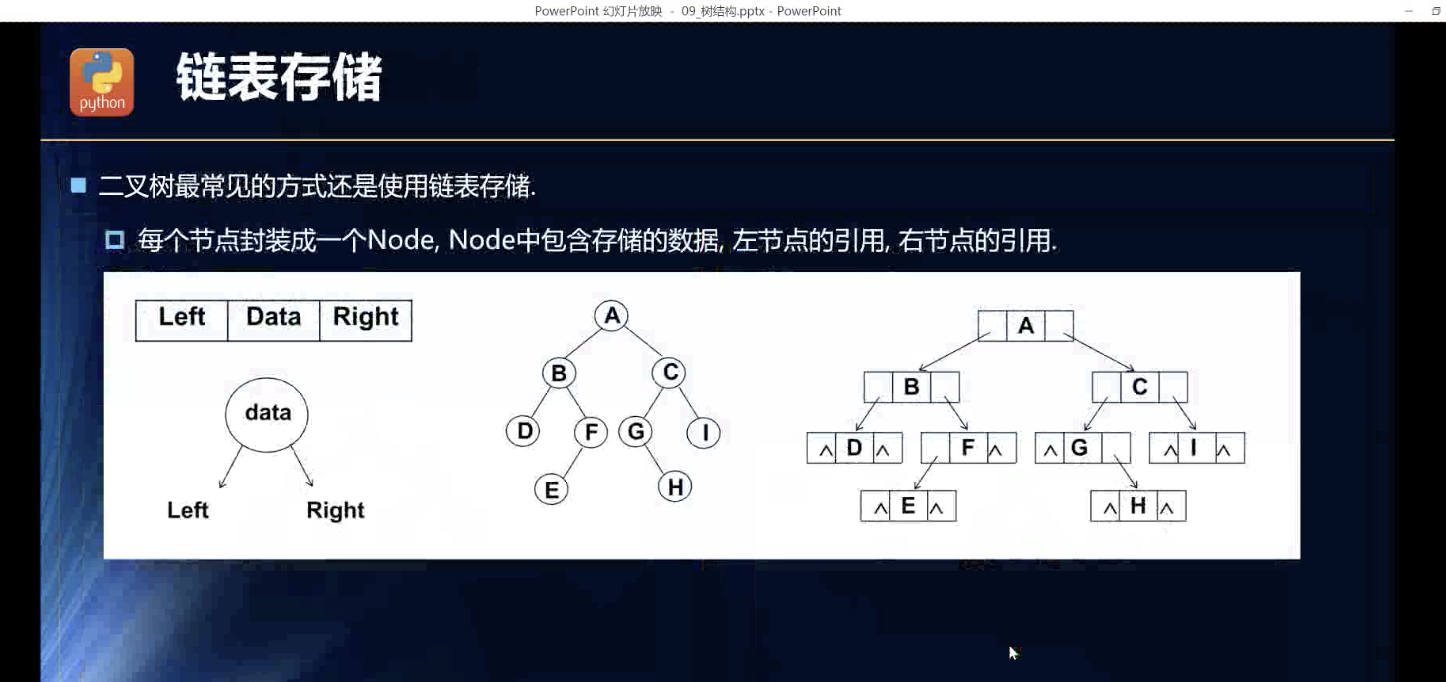
最终版的探索！就是如此。很像是递归的感觉。

二叉搜索树

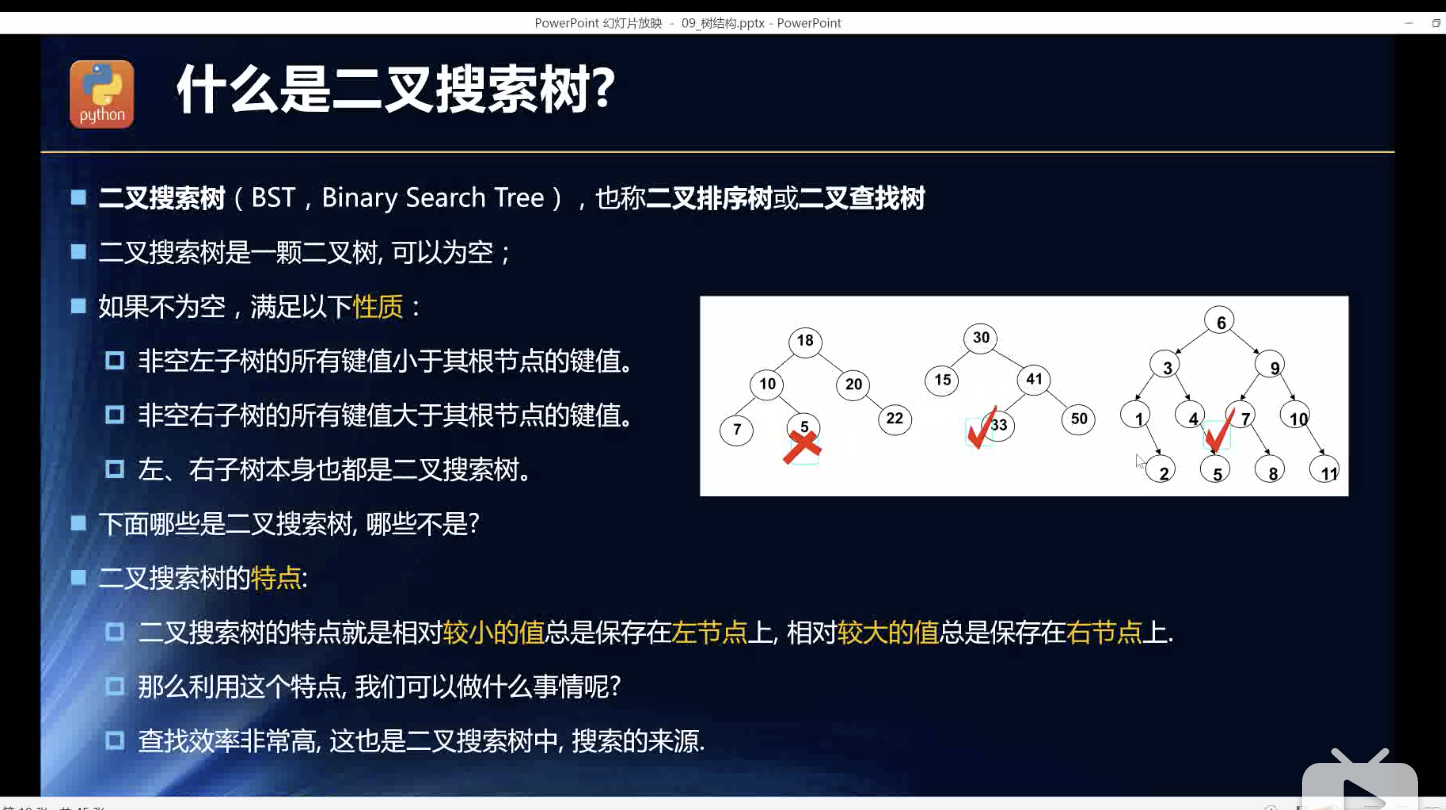
我只说一个规律：正三角形的三个点，左小，顶点大，右最大！如有缺失顶点，可虚拟补上一个。
最小值：最左下角的。最大值：最右下角的。
**

搜索性能强

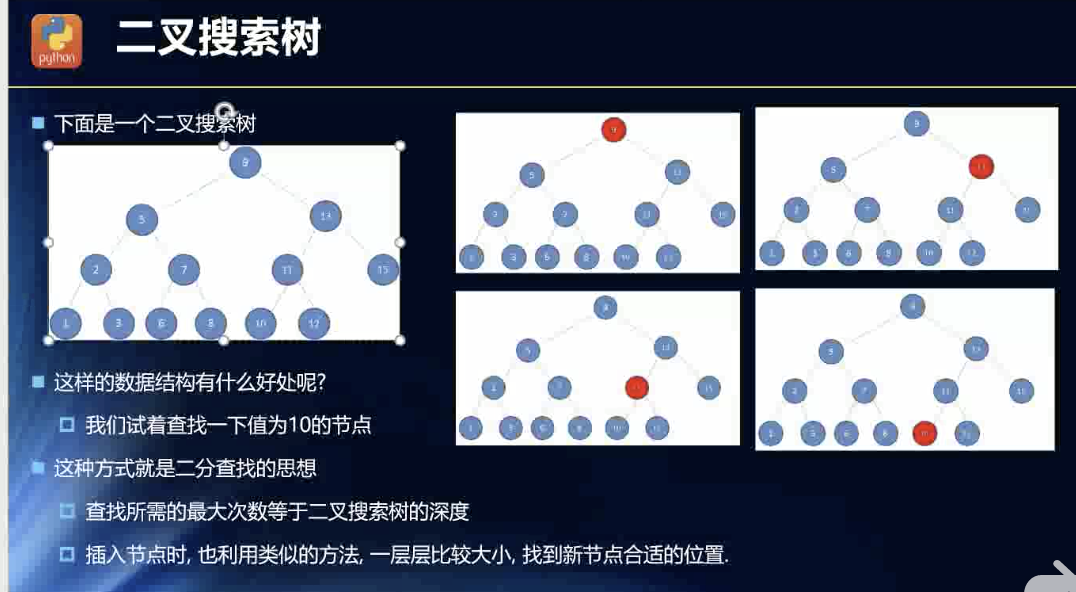
这让我想起了二分法了，一样的味道！
老师说了，二叉搜索树的低层就是二分法实现的。

二叉搜索树封装

一定要有根节点！

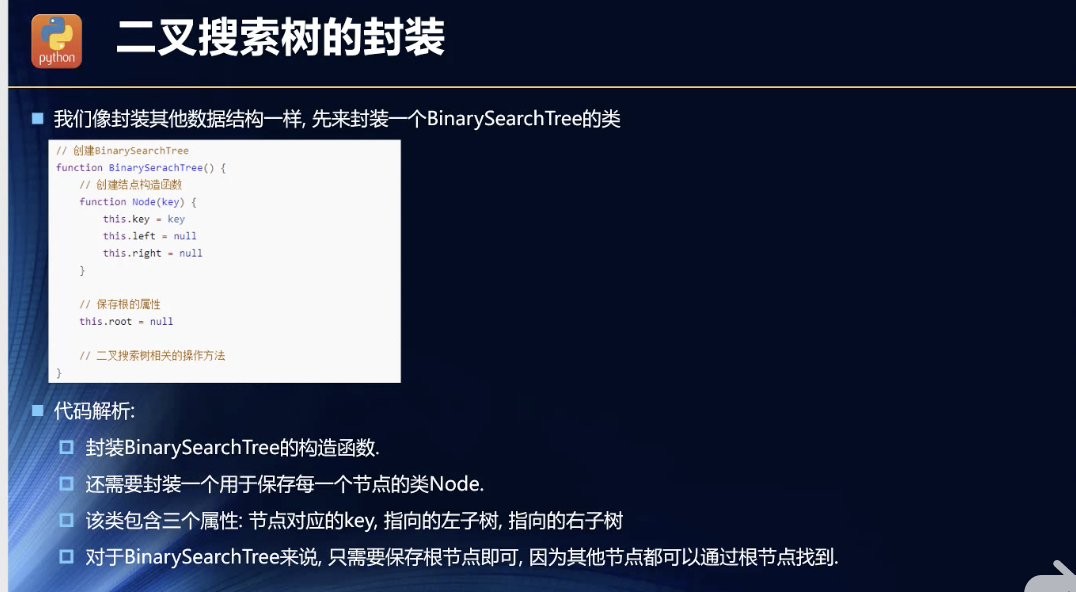
class Node {
    constructor(key, data) {
        if (typeof key !== "number") {
            throw new Error("Node 构造函数必须要有一个Number类型的key参数！");
        }
        this.key = key;
        data && (this.data = data);
        this.left = null;
        this.right = null;
    }
}
class BinarySearchTree {
    constructor(root) {
        this.root = root || null
    }
}

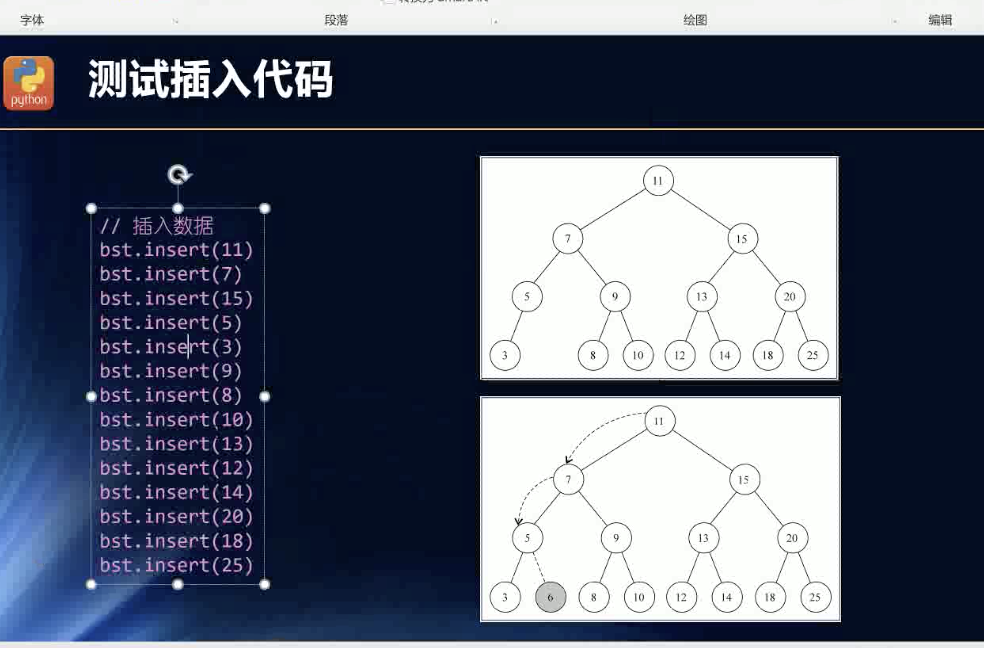
插入

说实在的，我原本认为的插入操作是，尽可能地按照从小到到的顺序进行插入的完美结果。什么意思？

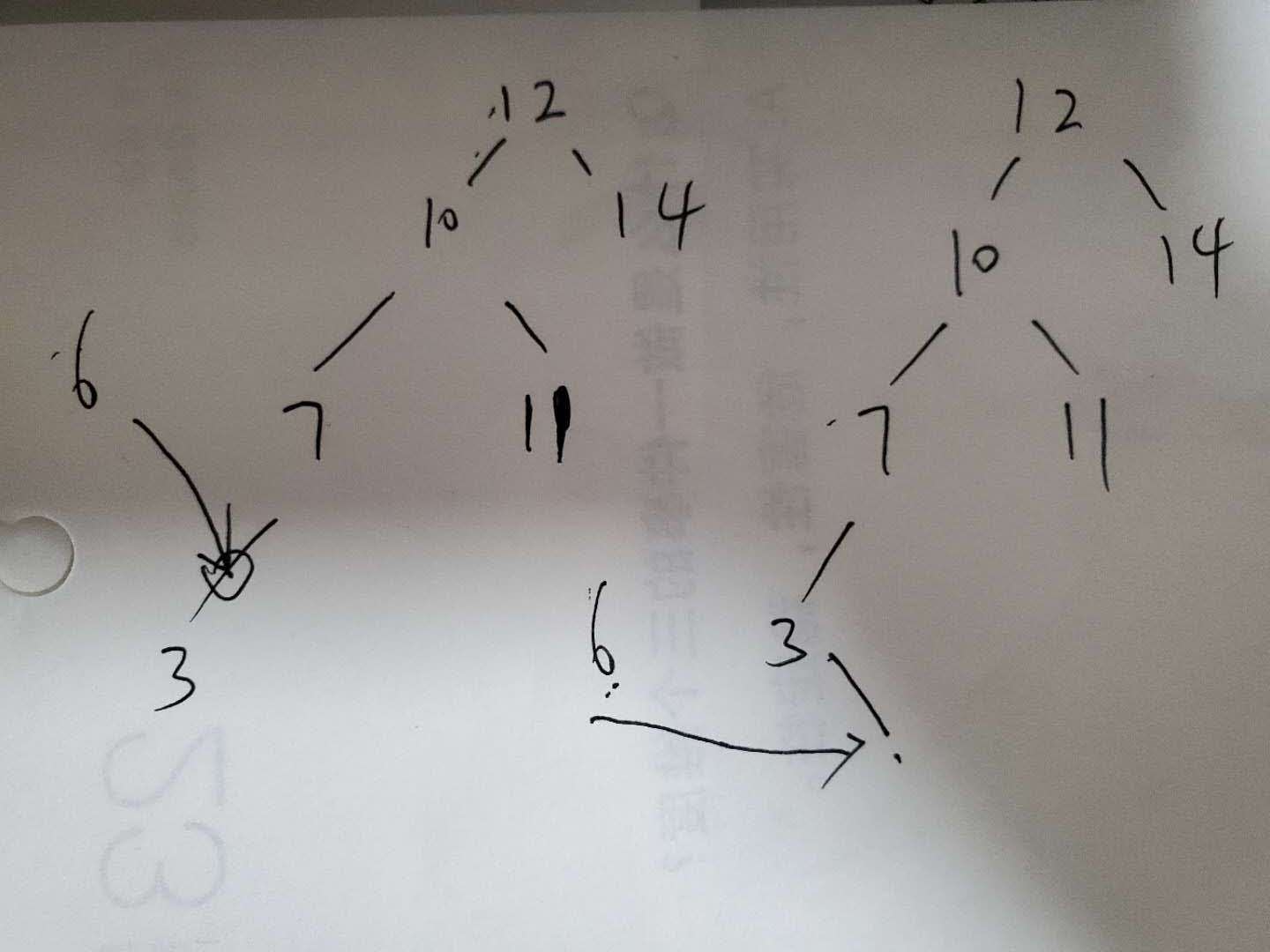
我想到的是左边的想法，所以我想复杂了，，，然后当时怎么实现都觉得不合理了。
然后直接就看老师的逻辑。才明白是右边的逻辑，这就简单了，要么while循环，要么递归了。

class BinarySearchTree {
    constructor(root) {
        this.root = root || null;
    }
    _insertNode(current, node) {
        if (current.key > node.key) {
            const {left} = current;
            if (left === null) return current.left = node;
            this._insertNode(left, node);
        } else {
            const {right} = current;
            if (right === null) return current.right = node;
            this._insertNode(right, node);
        }
    }
    insert(key, data) {
        const node = new Node(key, data);
        if (this.root) {
            this._insertNode(this.root, node);
        } else {
            this.root = node;
        }
    }
}
const binarySearchTree = new BinarySearchTree()
const arr = []
for(let i =0;i<10;i++){
    arr.push(Math.floor(Math.random()*100))
}
arr.map(
    (num,ind)=>binarySearchTree.insert(num,{id:ind})
)
console.log(binarySearchTree);

看老师的例子，加深一下，插入的规则！说明我对二叉树的理解还是有些不正确的！

遍历

先序遍历

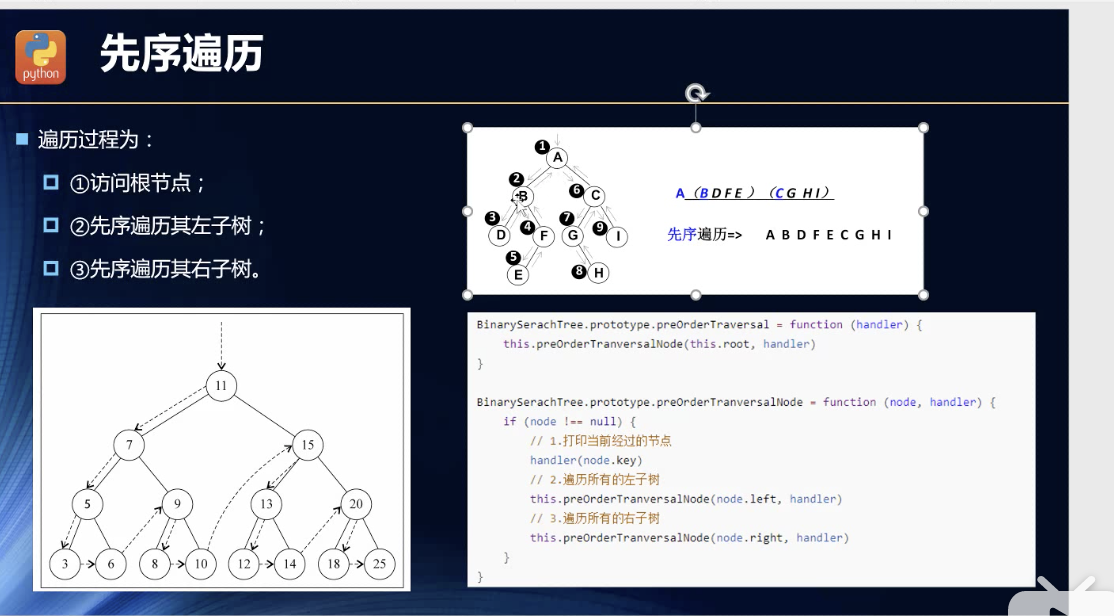
说真的，我真的自己想了好久，就是没想过递归的方向的。所以，除了用状态管理不断地暂存数据，然后再判断中循环，我是真的没想到其他的思路了。
拿来主义了，我好菜啊！新的套路了！递归！

给自己洗脑强化一番！递归，为什么更适合树？源于我上面的那个感觉，职能重合，长兄如父的感觉了。本就是一个个正三角形的子树组成的大树。嵌套的数据结构的时候，就用递归。
**

 //先序遍历
    preOrderTraversalNode(callback) {
        //先遍历好左节点，再遍历右节点：
        this._preOrderTraversalNode(this.root,callback)
    }
    _preOrderTraversalNode(node,callback) {
        //先遍历好左节点，再遍历右节点：
        if (node !== null){
            callback(node.key,node.data)   
            this._preOrderTraversalNode(node.left,callback)
          //其实我不能明白的是如何能先左同时又照顾层级，后右的？原来我又要复习一下栈结构了：
          //拿上面图的树做例子推导一下：
          11->7->
            5->(3->null->null)->3->
            5->(6->null->null)->
            5->7
            ->9->(8->null->null)->9->(10->null->null)
          ->9->7->11
          11->15->13->(12->null->null)->13->(14->null->null)->13->15
          ->20->(18->null->null)->20->(25->null->null)
            this._preOrderTraversalNode(node.right,callback)
        }
    }

递归没怎么如此抽象地用过，，，以前就是对很实在的嵌套的数据对象进行过处理。要加深这个套路了！

中序遍历

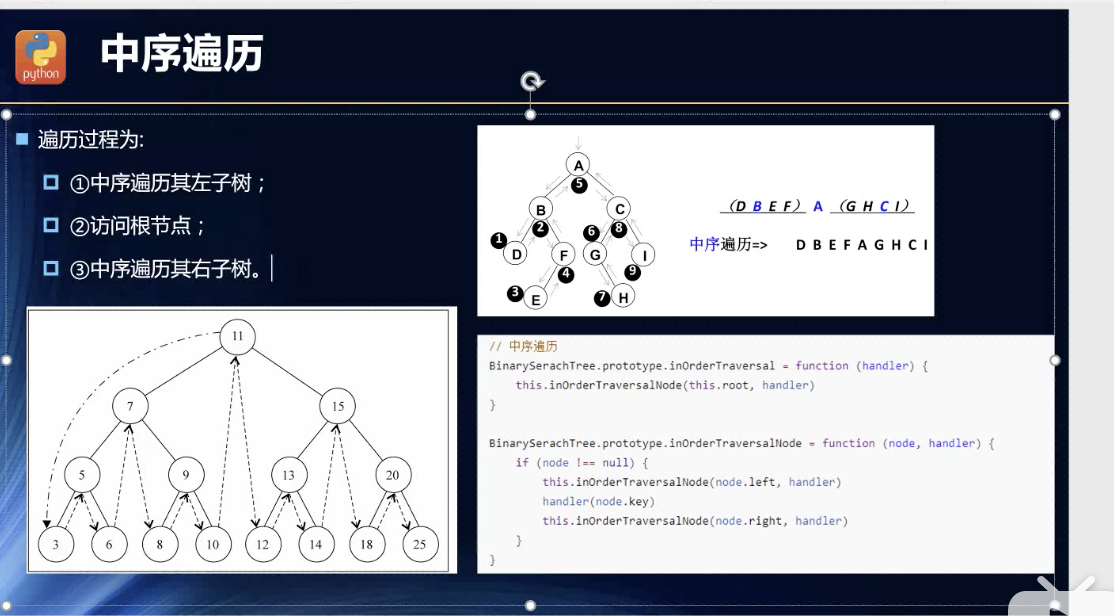
同样的套路：递归，会深层嵌套，不断入栈新函数！

         midOrderTraversalNode(callback) {
        this._midOrderTraversalNode(this.root, callback);
    }
    _midOrderTraversalNode(node, callback) {
        if (node) {
            this._midOrderTraversalNode(node.left, callback);
            callback(node.key, node.data);
            this._midOrderTraversalNode(node.right, callback);
        }
    }

后序遍历

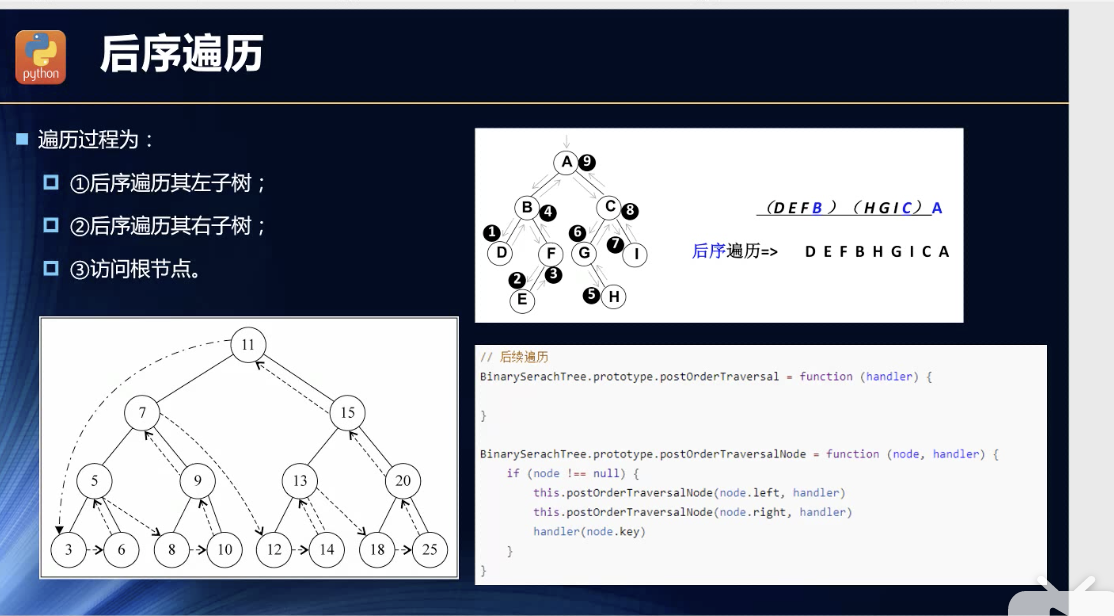
同样的套路：递归！

        postOrderTraversalNode(callback) {
        this._postOrderTraversalNode(this.root,callback)
    }
    _postOrderTraversalNode(node, callback) {
        if(node){
            this._postOrderTraversalNode(node.left,callback)
            this._postOrderTraversalNode(node.right,callback)
            callback(node.key,node.data)
        }
    }

总结

看路径，怎么画三角形的！
正序：顶点开始逆时针。
中序：左下点开始顺时针。
后续：左下开始逆时针。
关于递归，有了更深层的认识了，确实是很巧妙的，层层嵌套的！
想过试试尾递归，不过这种二叉树的形式，差了个反向的指针了！除非搞成双链表那种。如果想用尾递归，各个节点还需要加上个parent属性，其实加上这个属性，让我想起了关系型数据表里的一个专门的业务表了。

最大值最小值

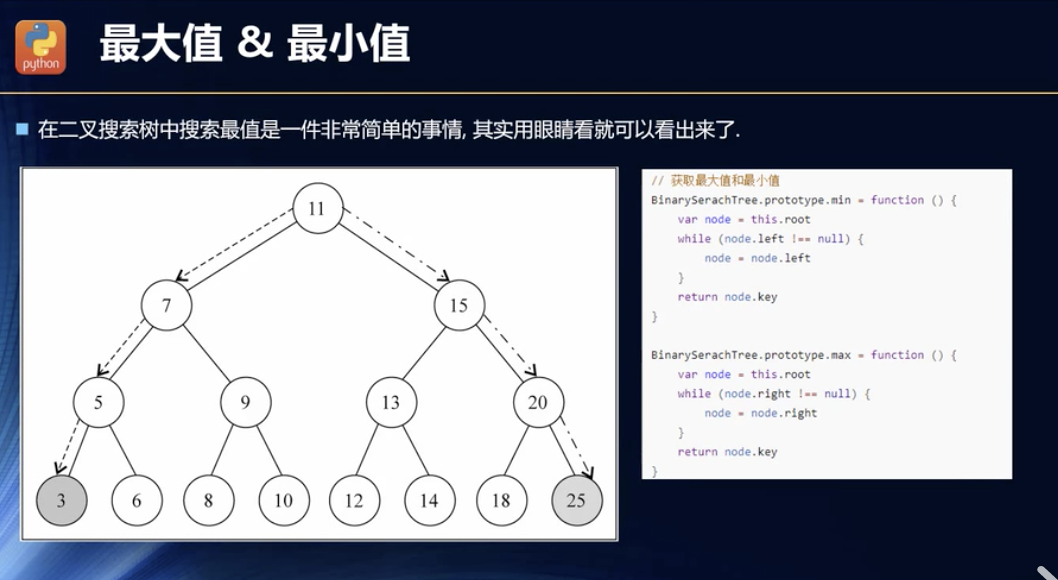
没啥可说的，最简单的视角是一个正三角是一个内部作用域，嵌套的三角形，越顶点的越极端。

         get max() {
        let current = this.root;
        if (current === null) return null;
        while (current.right) {
            current = current.right;
        }
        return current.key;
    }
    get min() {
        let current = this.root;
        if (current === null) return null;
        while (current.left) {
            current = current.left;
        }
        return current.key;
    }

搜索特定的值

         search(key) {
        return this._search(this.root, key);
    }
    _search(node, key) {
        if (node !== null) {
            if (node.key === key) return node;
            return node.key > key ?
                this._search(node.left, key) :
                this._search(node.right, key);
        }
        return null;
    }

不用递归的话：

  search(key){
    let current = this.root;
    if (current === null) return null;
    let res = null;
    while (current) {
      if (current.key === key) return res = current;
      current = current[current.key > key ? "left" : "right"];
    }
    return res;
  }

删除：复杂！！

分析

删除节点，我原本觉得很复杂，其实我也是没有思路了。就算当初自己想到了删除叶子节点之类的简单，到删除子节点的时候，依旧是一头雾水的。子节点的左右子节点们如何安排？？

其实当时是卡在这里了。如今再想一想，其实差的是一个标准，一个需求，一个安排而已。我甚至可以规定，左为尊，有左的优先左的节点重新添加到二叉树，然后右的再添加。也可以右为尊，甚至可以一层一层地左为尊或者右为尊的。如此就简单多了！
当然，以上只是我的预想意淫，后期打脸了，我也不会删了的。我不认为自己的想法不是一种需求啊！

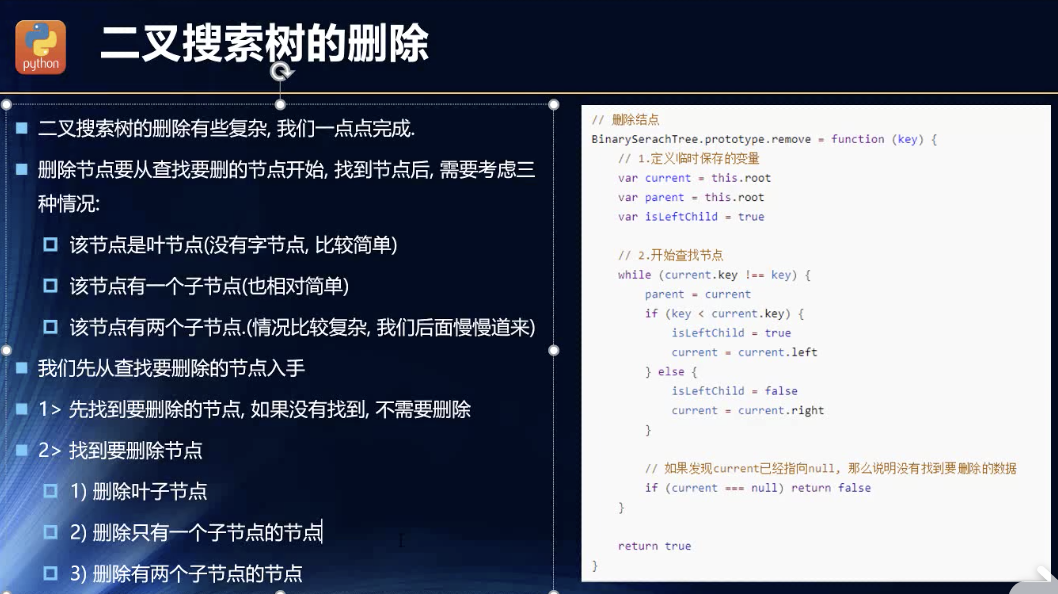
没有子节点

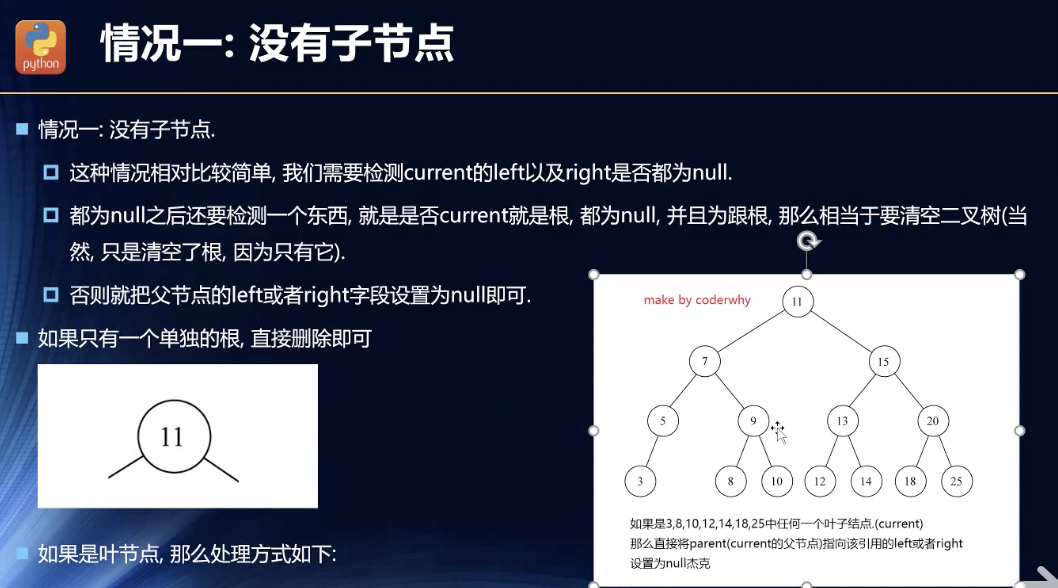
无论是什么情况，只要是根节点，那就不一样的！
这里也要分是不是根节点！

一个子节点

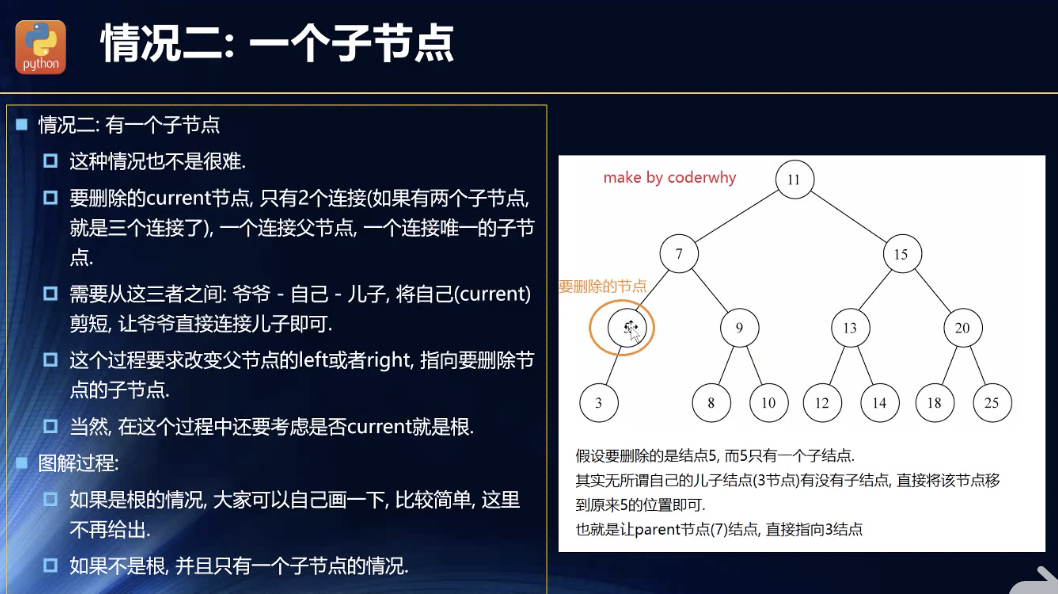
无论是什么情况，只要是根节点，那就不一样的！
这里也要分是不是根节点！

寻找删除节点

         _findNode1(key) {
        let parent = this.root, current = null;
        if (parent === null) return null;
        while (current === null) {
            if (parent.key === key) return {node: parent};
            const testKey = parent.key > key ? "left" : "right";
            const child = parent[testKey];
            if (child) {
                if (child.key === key) {
                    return {parent, child: testKey};
                } else {
                    parent = child;
                }
            } else {
                return null;
            }
        }
    }
//不递归与递归
    findNode(key) {
        return this._findNode(this.root, key);
    }
    _findNode(node, key) {
        if (node === null) return null;
        if (node.key === key) {
            return {node};
        }
        const test = node.key > key;
        const testKey = test ? "left" : "right";
        const child = node[testKey];
        if (child) {
            if (child.key === key)
                return {parent: node, child: testKey};
            return this._findNode(child,key);
        } else {
            return null;
        }
    }
//注意我的返回结果的形式： null , {node},{parent,child:'left'}，涉及到接口了。

删除简单节点——叶节点或者节点本身只有一个子节点

        _removeRoot(node) {
        if (node.right === null && node.left === null) {
            this.root = null;  //木有子节点
            return true;
        }
        if (node.right && node.left) { //两个子节点
        } else { //一个子节点
            this.root = node.right || node.left;
            return true;
        }
    }
    remove(key) {
        const res = this._findNode1(key);
        if (res === null) return false;
        const {node, parent, child} = res;
        if (node) {
            //删除的是根节点！
            return this._removeRoot(node);
        } else {
            //node 与 parent不共存的：
            //1.没有子节点：
            const node = parent[child];
            if (node.right === null && node.left === null) {
                parent[child] = null;
                return true;
            }
            if (node.right && node.left) { //1个子节点
            } else { //两个子节点
                parent[child] = node.right || node.left;
                return true;
            }
        }
    }

这里对一个子节点的时候，为啥要直接赋值父节点的同样的left / right属性呢？我用上面的图中的树进行了演绎，就加深了感觉了，树的每一个节点都是二分法的裁判，每一个节点其实都是一个过滤器，过滤掉比他大的，比他小的。
我突然觉得这种过滤器的设计真的会很有用的，虽然目前我暂时木得想法。

删除节点有两个子节点

演绎，规律

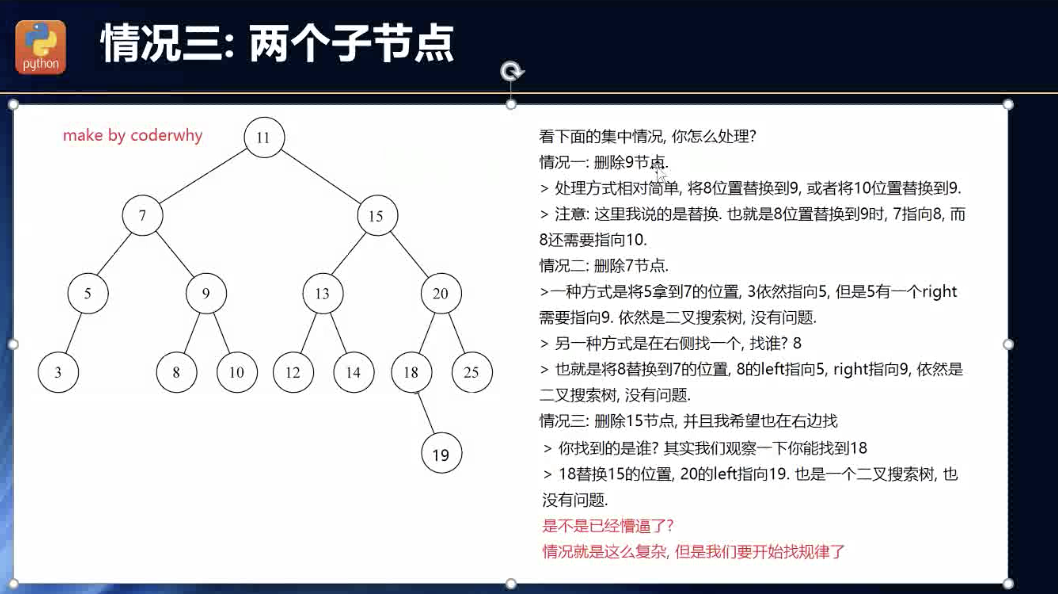
其实，看这个ppt，演绎了一下，才真的是对二叉搜索树进行了构建概念的深入了。前面都是普通认知层面。
上面我恰好对节点的所谓的过滤器机制进行了构建了。我发现这次演绎，其实就是说的这个过滤器机制：

 情况1：
 9节点 ： 左边的都比9小，并且比7大。右边的都比9大！
 情况二：
 7节点：左边的都比7小，最大为5。右边都比7大，最小为9。
 情况三：
 15节点：左边的都比15小，比11大.右边的都比15大，最小为19。

删除的那个节点，是要当过滤器的存在，替补的节点，必须要做到：

1. 比删除位置的左节点链接的所有节点都大。
2. 比删除位置的右节点链的所有节点都小。

比如左子节点作为根节点的子树的最大值，或右子节点作为根节点的子树的最小值。

删除节点是其父节点的left/right属性，分情况演绎：
left——满足条件1，2：
这个节点根据情况的不同，可以是删除节点的左子节点或左子节点构成树的最大值（相对应的断裂的子节点也需要拼接的），或者是删除节点的右子节点组成的树的最小值！
right——满足条件1，2：
这个节点根据情况的不同，可以是删除节点的左子节点组成的树的最大值，或者是删除节点的右子节点组成的树的最小值！

如果，要从左节点链中拿一个节点，那就是其中的最大值的节点！
如果，要从右节点链中拿一个节点，那就是其中的最小值！

其实根本结论就是：左子节点作为根节点的子树的最大值，或右子节点作为根节点的子树的最小值。
**

规律

**

删除封装完整版

**

 //找到替换的元素：前驱/后继
    findPrecursorOrSuccessor(node) {
        const {left, right} = node;
        let precursor = left, successor = right, parent;
        if (precursor) {
            while (precursor.right) {
                parent = precursor;
                precursor = precursor.right;
            }
            //预处理，替换的节点跟它的父节点的交接工作：
            if (parent) {
                parent.right = precursor.left;  //有木有值都对！
            }
            return {precursor, parentNeed: Boolean(parent)};
            //这是区分是否是直接为删除节点的直接left节点的
        } else {
            while (successor.left) {
                parent = successor;
                successor = successor.left;
            }
            //预处理，替换的节点跟它的父节点的交接工作：
            if (parent) {
                parent.left = successor.right;  //有木有值都对！
            }
            return {successor, parentNeed: Boolean(parent)};
            //这是区分是否是直接为删除节点的直接right节点的
        }
    }
//回归删除操作的那部分：完整版
 _removeRoot(node) {
        if (node.right === null && node.left === null) {
            this.root = null;  //木有子节点
            return node;
        }
        if (node.right && node.left) { //两个子节点
            const {precursor, successor,parentNeed} =
                this.findPrecursorOrSuccessor(node);
            const newNode = precursor || successor;
            if (parentNeed){
                newNode.right = node.right
                newNode.left = node.left
            }else{
                precursor && (precursor.right = node.right);
                successor && (successor.left = node.left);   
            }
            this.root = newNode;
            return node;
        } else { //一个子节点
            this.root = node.right || node.left;
            return node;
        }
    }
    remove(key) {
        const res = this._findNode1(key);
        if (res === null) return false;
        const {node, parent, child} = res;
        if (node) {
            //删除的是根节点！
            return this._removeRoot(node);
        } else {
            //node 与 parent不共存的：
            //1.没有子节点：
            const node = parent[child];
            if (node.right === null && node.left === null) {
                parent[child] = null;
                return node;
            }
            if (node.right && node.left) { //2个子节点
                const {precursor, successor, parentNeed} =
                    this.findPrecursorOrSuccessor(node);
                const newNode = precursor || successor;
                if (parentNeed) {
                    newNode.left = node.left;
                    newNode.right = node.right;
                } else {
                    precursor ? (precursor.right = node.right) :
                        (successor.left = node.left);
                }
                parent[child] = newNode;
                // console.log(parent, "parent", newNode, "new");
                return node;
            } else { //1个子节点
                parent[child] = node.right || node.left;
                return node;
            }
        }
    }