二叉搜索树有缺——红黑树

优点

搜索，查询效率高！快速插入和删除。关键影响的因素是深度，也就是层级！O(log(n))。

缺点

插入的数据的大小次序都会影响二叉树的分布。真实开发，插入的顺序和大小不可控的。深度会加深！深度涉及到了效率！尽可能地均匀分布！

非平衡二叉树其实就是一个链表了。
**

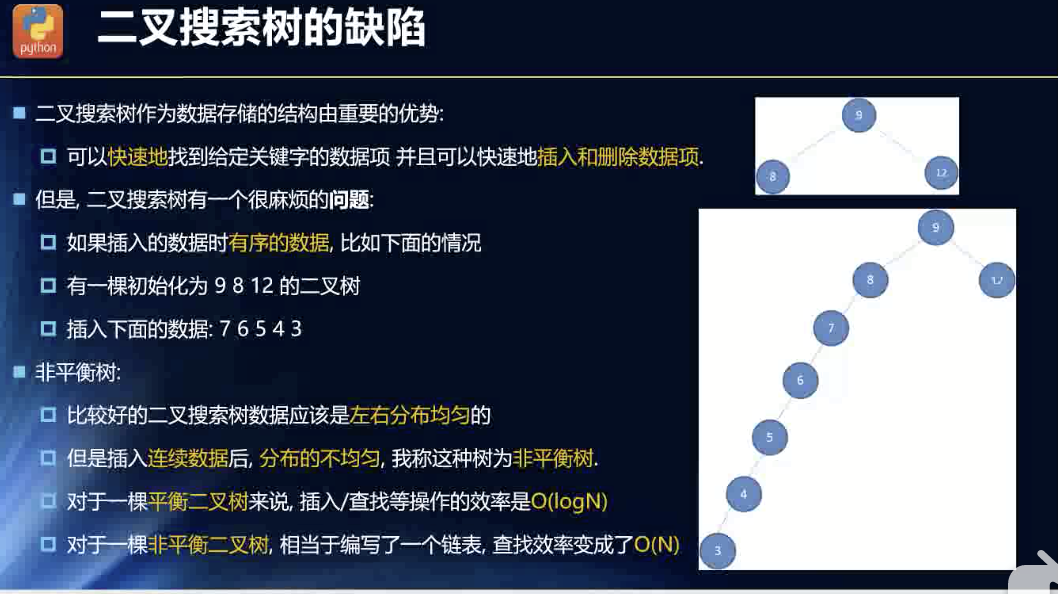
问题：如何保持二叉树的平衡性？

红黑树我暂时不清楚，但是我如果想要做平衡树，我就存储两个属性，所有的左右子节点的个数统计数量，得有一个差值范畴，个数之间差值超过多少，需要人为操作，改变些条件来进而影响到要删除的或者要插入的节点的插入位置。
想到操作的思路，或许是通过修改根节点，比如左边的子节点太多了，反应了根节点太小了！右边的也是同理！但是依旧是个一般的控制，很宏观，无法微观调控了。微观调控体现在了所有的左节点，所有的右节点，而改变根节点直接改变的是左子节点树和右子节点树的节点数，无法直接改变左子节点数与右子节点数。
要微调，就要想那个正三角形了。尽可能地构成三角形，而不是一条长边。

操作的角度入手点，目前只想到两个点：

• 根节点的选择。根节点保证了左右节点组成的子树的节点数量！
• 数据插入的顺序。顺序越是递增或递减地数据规律，越是垃圾！当然，想到那个三角形，我就知道必须要先插个顶点，也就是middle 大小的，然后再插入个紧贴顶点的大一点或小一点的值。比如4，5，6。插入顺序是5，x,y。