排序算法

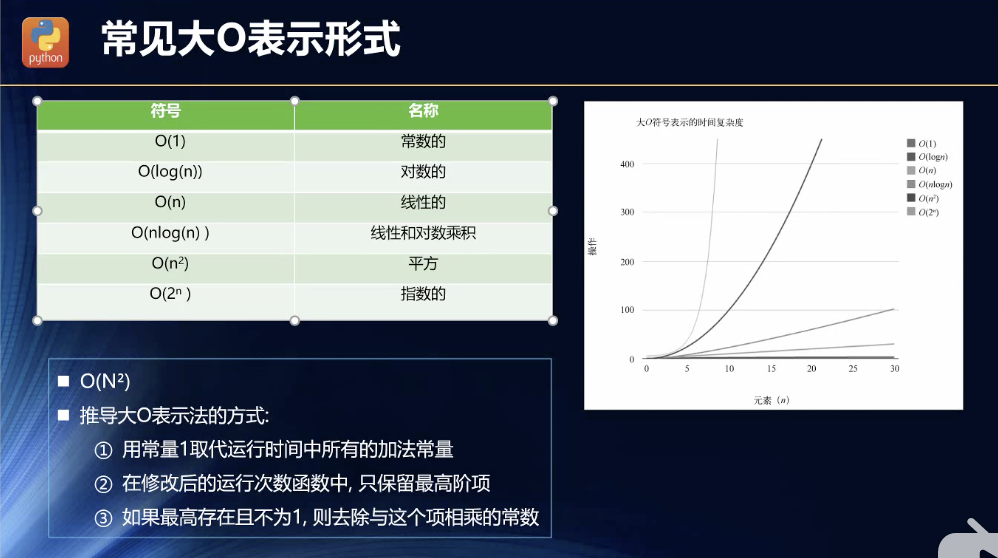
引子

人来执行排序的话，是多线程的，而且主动自觉的，可以兼顾前后的人的高矮的。

计算机来执行排序，就要一个一个地遍历了。可以模拟执行逻辑，但是控制对象只能是一个进行，而不是每个人都有主观能动性，很聪明的。

封装了一个类，存储数据和调用各种排序方法的类

class ArrayLists {
    constructor(arr=[]) {
        this.items = arr
    }
    insert(val){
        this.items.push(val)
    }
    toString(){
        return this.items.reduce(
            (a,b)=> a + (a?' -> ':'')+b,''
        )
    }
}
const lists = new ArrayLists([2,534,23,24,67,2,34,3,3,64])
console.log(lists.toString());

冒泡排序

记得第一次会写数组中找最大值，就是用的如此的思路。找个变量，作为指针做记录。我之前的排序算法说到底也是冒泡排序了，只不过我一次遍历，找的是最大加最小值，然后最大值的index位，跟length-1的那个位的数据互换位置，同理，最小的值的index的位跟0位的数据互换位置，然后二次遍历，从1位遍历到length-2位，找到最大，最小的下标，跟length-2和1的位置的数据互换位置。以此类推，，，

这是我对冒泡排序的优化，这其中的bug就是换位的时候，是不是换掉了正好是指针指向的最大值or最小值。否则，，，
我还有一种优化，专门优化重复多个最大值，最小值们的位置变换的，，，当时，考虑到如此的性能反而会拉胯的，干脆我就放弃了因为重复多个最大值导致的状态管理的逻辑开销的设想了。

先看下正统的冒泡排序如何的吧！

很简单：

 // 冒泡排序
    bubble() {
        let count = 0, {items} = this;
        while (count < items.length - 2) {
            for (let i = 0; i < items.length - 1 - count; i++) {
                if (items[i] > items[i + 1]) {
                    const min = items[i + 1];
                    items[i + 1] = items[i];
                    items[i] = min;
                }
            }
            count++;
        }
        return items;
    }

有问题的冒泡排序优化

//优化冒泡排序,有问题的！
    bubbleFix() {
        let start = 0, {items} = this, end = items.length - 1;
        while (start <= end) {
            console.log(start, end);
            let min = items[start], max = min,
                minIndex = [start], maxIndex = [start];
            for (let i = start; i <= end; i++) {
                const n = items[i];
                if (min > n) {
                    min = n;
                    minIndex = [i];
                } else if (min === n && i !== start) {
                    minIndex.push(i);
                }
                if (max < n) {
                    max = n;
                    maxIndex = [i];
                } else if (max === n && i !== start) {
                    maxIndex.push(i);
                }
            }
            const copy = [];
            console.log(min, minIndex, items);
            minIndex.map(
                v => {
                    if (v === start) return start += 1;
                    const startV = items[start];
                    copy[start] = v;    //这里的逻辑有问题的
                    items[start] = min;
                    items[v] = startV;
                    start++;
                }
            );
            console.log(items, start, end, 888, max);
            for (let i = maxIndex.length - 1; i >= 0; i--) {
                let ind = maxIndex[i];
                if (ind !== end) {
                    if (copy[ind] >= 0) {
                        ind = copy[ind];   //这里的逻辑有问题的！
                    }
                    items[ind] = items[end];
                    items[end] = max;
                }
                end -= 1;
            }
            console.log(start, end, 9999);
        }
    }

当然，如果我不搞重复的最大值，最小值，基本就不会出错了。我就不写那个简单的了。
想了很久，自己演绎了一下，暂时得出问题出在，如果重复的很多，同时连续替换的位置，都是max的原位置，就会难保copy可以顺利跟踪到位的！
如何确保替换后的映射呢？字典？？

bubbleFix() {
        let start = 0, {items} = this, end = items.length - 1;
        while (start <= end) {
            console.log(start, end);
            let min = items[start], max = min,
                minIndex = [start], maxIndex = [start];
            for (let i = start; i <= end; i++) {
                const n = items[i];
                if (min > n) {
                    min = n;
                    minIndex = [i];
                } else if (min === n && i !== start) {
                    minIndex.push(i);
                }
                if (max < n) {
                    max = n;
                    maxIndex = [i];
                } else if (max === n && i !== start) {
                    maxIndex.push(i);
                }
            }
            const copy = [];
            console.log(min, minIndex, items);
            minIndex.map(
                v => {
                    if (v === start) return start += 1;
                    const startV = items[start];
                    copy[start] = v;    //这里的逻辑有问题的
                    items[start] = min;
                    items[v] = startV;
                    start++;
                }
            );
            console.log(items, start, end, 888, max);
            for (let i = maxIndex.length - 1; i >= 0; i--) {
                let ind = maxIndex[i];
                if (ind !== end) {
                    if (copy[ind] >= 0) {
                        ind = copy[ind];   //这里的逻辑有问题的！
                    }
                    items[ind] = items[end];
                    items[end] = max;
                }
                end -= 1;
            }
            console.log(start, end, 9999);
        }
    }

修改测试暂时没问题的魔改冒泡排序：

    bubbleFix() {
        let start = 0, {items} = this, end = items.length - 1;
        while (start <= end) {
            console.log(start, end);
            let min = items[start], max = min,
                minIndex = [start], maxIndex = [start];
            for (let i = start; i <= end; i++) {
                const n = items[i];
                if (min > n) {
                    min = n;
                    minIndex = [i];
                } else if (min === n && i !== start) {
                    minIndex.push(i);
                }
                if (max < n) {
                    max = n;
                    maxIndex = [i];
                } else if (max === n && i !== start) {
                    maxIndex.push(i);
                }
            }
            const copy = {},copy1={};  //这里用了双指针，保证改动的指向的动态一致性
            //console.log(min, minIndex, items);
            minIndex.map(
                v => {
                    if (v === start) return start += 1;
                    const startV = items[start];
                    if (startV === max){
                        if(copy1[start]===undefined){
                            copy[start] = v
                            copy1[v] = start
                        }else{
                            copy[copy1[start]] = v
                            copy1[v] = copy1[start]
                        }
                    }
                    items[start] = min;
                    items[v] = startV;
                    start++;
                }
            );
            //console.log(items, start, end, 888, max);
            for (let i = maxIndex.length - 1; i >= 0; i--) {
                let ind = maxIndex[i];
                if (ind !== end) {
                    if (copy[ind] >= 0) {
                        ind = copy[ind];
                    }
                    items[ind] = items[end];
                    items[end] = max;
                }
                end -= 1;
            }
            //console.log(start, end, 9999);
        }
    }

官方版本解释

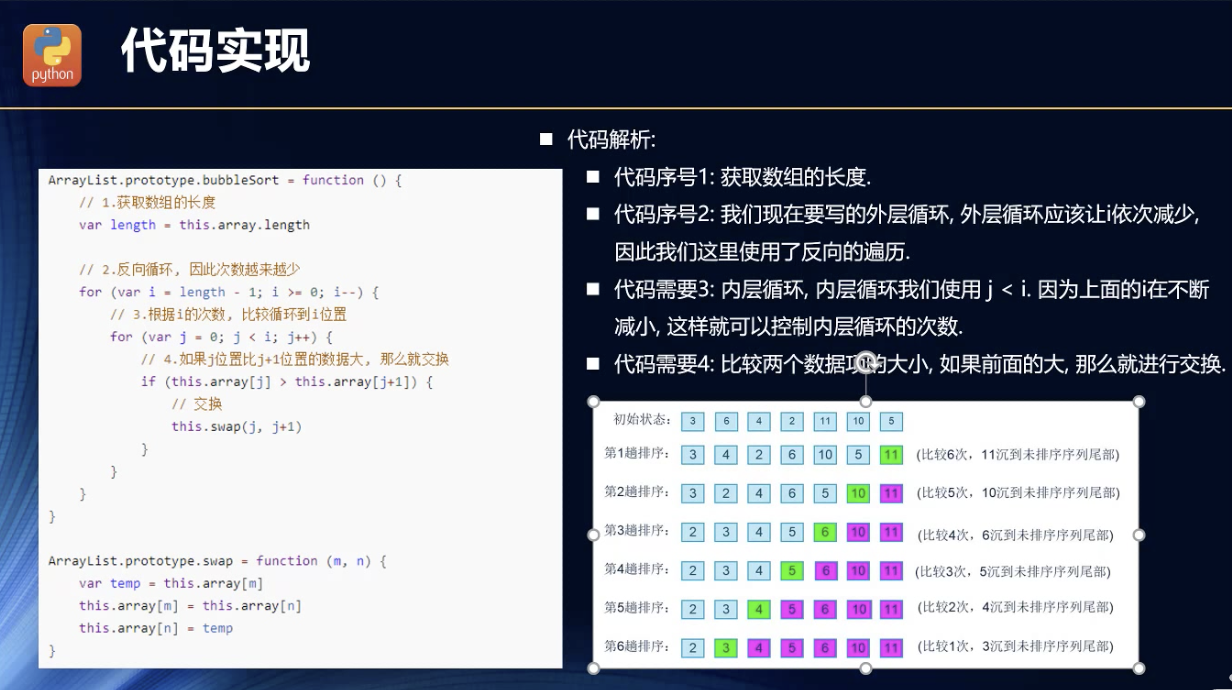
分析过程效率

交换次数，平均下来就是n*(n-1)/2/2。

就算我优化了冒泡排序，也不过是变小了那个n^2的那个小常量。所以，冒泡排序很垃圾的。

选择排序

我看完之后， 觉得老有意思了。很熟悉，就是我对冒泡排序的改进！
跟冒泡排序的区别在于用了指针，减少了交换次数！仅此而已！

官方思路的代码

         selectionSort() {
        const {items} = this;
        let min = 0, start = 0;
        while (start < items.length - 1) {
            for (let i = start; i <= items.length - 1; i++) {
                if (items[min] > items[i]) {
                    min = i;
                }
            }
            let v = items[min];
            items[min] = items[start];
            items[start] = v;
            start +=1;
            min = start;
        }
    }

这里我就要说了，上面我的魔改的冒泡排序，其实就是选择排序的。只不过我的选择排序，魔改的太多了，增加了更多的状态控制和判断，因为我最近看了些计算机原理的东西，知道逻辑运算要用到门，状态管理的代价就是逻辑运算的开销增加了。
我前几天刷leetcode的时候，我也尝试过不同的解法，很多都是自以为，增加了很多的状态控制，减少了不必要的遍历开销，实则发现，由此增加的状态控制的逻辑运算的开销反而更大了，好无奈啊！

所以，对于比较细枝末节的优化，减少逻辑运算的成本更优。而遍历的成本，如果能从大O表示法的量级上减少，那才是真的优化了，而不是负优化！

效率

其实在循环遍历的流程上，跟冒泡排序是一个样子的。时间复杂度依旧是O(n^2),只不过减少了交换次数，比冒泡排序更快点而已。
过程推导，类同于冒泡排序！

插入排序

• 很重要！
• 最快的简单排序！
• 高级排序逻辑的基础！

理念

无序变有序！优势滚雪球！
我突然想，后续可以用二分法找到自己的位置，会更快的！这算是某种高级排序算法的思路么？

官方思路写的代码

  //插入排序
    insertSort(){
        const {items} =this
        let count = 1
        while (count <= items.length-1){
            for (let i=count;i>=1;i--){
                const current = items[i],last=items[i-1]
                if(current < last){
                    items[i] = last
                    items[i-1]=current
                } else {
                    break;
                }
            }
            count++
        }
    }

加入二分法优化尝试失败

可以用二分法很快确定插入的位置，但是还是要一个个地交换值变换过来的。少了判断逻辑了，但是交换赋值这步怎么也少不了了。

 insertSortFix() {
        const {items} = this;
        let count = 1;
        while (count <= items.length - 1) {
            const v = items[count]
            if (count === 1){
                if (v<items[0]){
                    items[1] = items[0]
                    items[0] = v
                }
            }else {
                const x = (start,end)=>{
                    const mid = Math.round((start+end)/2)
                    if(items[mid]>v ){
                        if(items[mid -1]<=v){
                            for (let i=count;i<=count;i++){
                                //这里还是要重复原本的方法的操作了，，，跟没优化一个样子了！
                                //二分法这里并可以快速定位，但是插入和删除操作，依旧跟原来的
                            }
                        }
                    }else {
                    }
                }
            }
            count++;
        }
    }

效率

从实现的思路上看，就觉得跟冒泡，选择一个量级的，两层嵌套循环，虽然中间细节会更省，但是双层遍历没跑了！

希尔排序

说真的，前面的简单排序就是我所能想到的硬解的基本逻辑了。真的是没法优化的！挺期待如何跳过这个量级的！因为普遍性的算法面向的是一种平均性的数据现实，唯有傻瓜式地硬解，遍历！

历史

我强行让自己想，，，结果没有想出来不用嵌套遍历的思路，算了，拿来主义了！

插入排序的编排

抛出思路：
嵌套的内层遍历如何优化？？当初我想到了二分法，但是只能找到位置，插入的动作依旧是要一个个地遍历过去。

希尔排序的思路

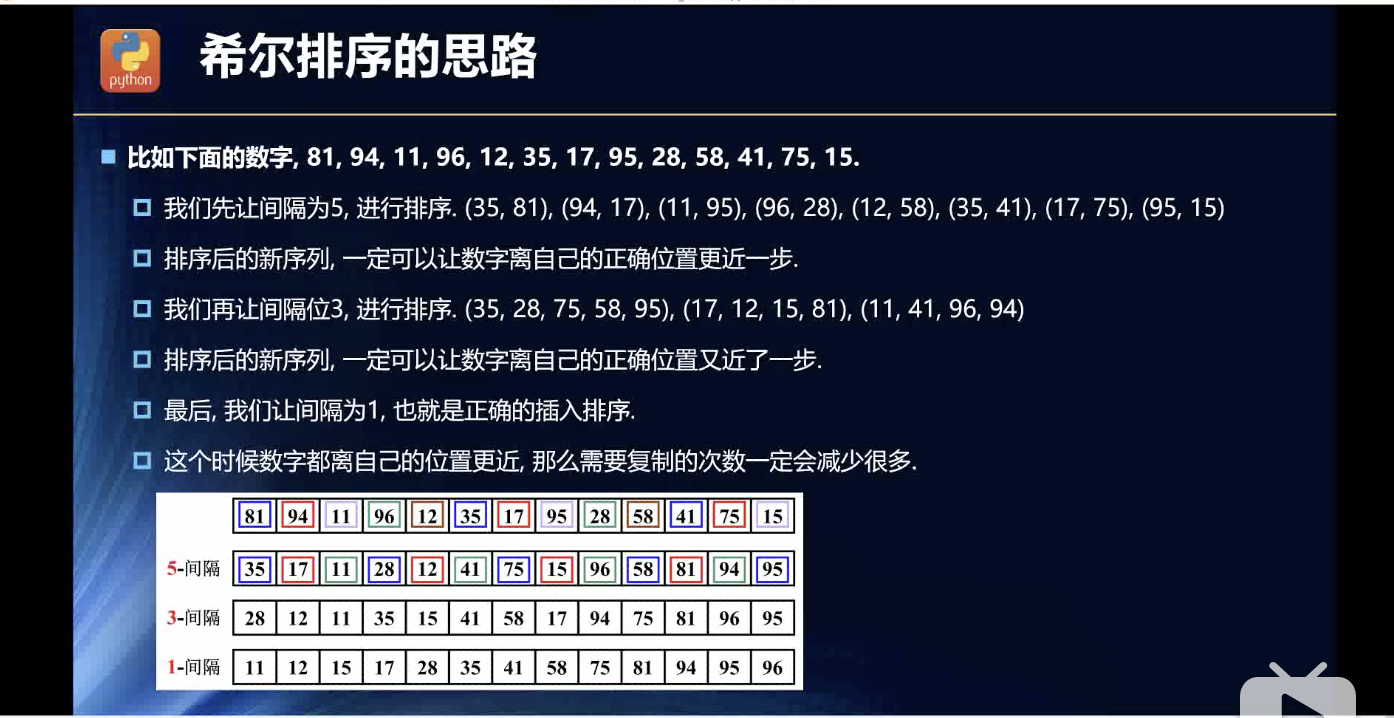
这，，，算是一种游戏哲学了。
让无序变为有序，硬解粗暴的哲学就是，完全彻底深度，想到了图的遍历里的深度优先了，正是因为要的是一个一个节点的完全深度地确认，所以才有了嵌套遍历！
而这种算是广度优先的感觉，每次遍历，所有的节点都是猪脚，都在努力向着最终各自的位置接近！这就是跳出圈子的感觉了！
之前我也是讲究硬解，从无序到有序，从一到二，到多，这木的办法不嵌套遍历啊！优点是唯一确定性！缺点是其他的点木得参与改变现状！

间隔或者叫增量定多少？

在我看来，奇数比较好，毕竟容易余出来余数，每次排序跟上一次排序的index范围都尽量不重合最好。就跟哈希表时候，想要分布均匀，最好用质数做那个指数的底一种感觉！

官方思路的代码实现

我自己写的 ：

            shellSort(){
        let {items} = this
        const {length} =items
        let gap = Math.floor(length/2)
        let count1 = 0   //计数基本的小循环的次数的！
        while (gap >=1){
            const max = Math.round(length/gap)
            for (let i=0;i<=max;i++){
                let count = i+ gap
                while (count<=length-1){
                    for (let j=count;j>=gap;j-=gap){
                        const current = items[j]
                        if(current < items[j-gap]){
                            items[j] = items[j-gap]
                            items[j-gap] = current
                        }else {
                            break;
                        }
                    }
                    count1++
                    count += gap
                }
            }
            gap = Math.floor(gap/2)
        }
        console.log(count1);
    }

然后看了一下老师的实现，觉得又是另一个味道了，然后我就觉得改一下，改成如此的了，有意思的事儿来了：

         shellSort1(){
        //尝试写法不一样：
        const {items}=this
        const {length} =items
        let gap = Math.floor(length/2)
        let count = 0
        while (gap>=1){
            for (let i=0;i<length;i++){
                for (let j=i;j>=gap;j-=gap){
                    const current = items[j]
                    if(current<items[j-gap]){
                        items[j] = items[j-gap]
                        items[j-gap] = current
                    }else {
                        break;
                    }
                }
                count++
            }
            gap = Math.floor(gap/2)
        }
        console.log(count);
    }

疑问

这两个count竟然会不一样！同样的逻辑！
随机生成100以内的正整数31个，然后前者的计数为575，后者为124！！是这两个count计数的循环的含义尺度有偏差？？

拆解：

影响次数的：gap,length都一样！
最外一层的遍历同等！
外二层遍历那里出现了差异：
第二种的方法的遍历很明显，从0到length-1，依次遍历过去。
第一种方法是：从0到max，依次遍历，这个max表明了，gap抽出来了的几个组的遍历。
差异在这里！最内层的遍历逻辑等同，但是数据量都变了！
因为第二层出现了差异，所以第三层的数据量变了，都变了！

我其实有些明白了，我的第一种的方法虽然基本的循环次数大,但是循环的第二层那里的循环数量级小！而第二种方法就是反过来的模式！这如何影响后续的遍历，我是有些头大了，遍历次数与每次遍历的数量级共同决定了效率的！
挺有意思的，按照惯例，我还是选遍历次数少的吧。。。

效率

没被证明出来，，，
比普通的快是一般现象！重要的是历史原因，突破了传统的我认为的所谓的深度优先的战略了！

快速排序

一句话，很重要！

思路

思路确实很简单，但是没有感觉了，需要写代码试试！

如何进行第二步？

[2,4,34,4,20,5,8,95,23,18]
比如选了8：
8跟最后一位交换：
[2,4,34,4,20,5,18,95,23,8]

生成两个指针，left，right,各自从0，倒数第二位向右，左运动，跟8做比较：
left : 2  < 8 ,不管，left=4；
right : 23 >8 ,不管，right = 95 ；
不管；left = 34 ,right = 18;
right 不管,riight=5。left 大于8，要改动！等待right<8，right=5,符合！34跟5互换！
left=4,right=20
left不管，left = 20 ，right = 20，这时候，8跟20交换！

逻辑是左边递增找比枢纽值大的一个数，右边递减找比枢纽小的一个数，两者互换！
当left = right时，如果指向值比枢纽大，跟枢纽互换，否则跟right指向值的下一位比较，不相等就直接交换。相等再找下一位，直到不相等或最后不操作！

如何选分治的数？

选的数，最好的是选所有数中的中间大小的数。尽量接近，这个应该很容易明白，最小或最大的都会增加第二步的消耗！

找到枢纽代码

        //写一个两个位置的交换函数，太难看了：
        exchangeValue(ind1, ind2, arr) {
        const v = arr[ind1];
        arr[ind1] = arr[ind2];
        arr[ind2] = v;
    }

          //找到枢纽：
    initMid(left, right, arr) {
        const mid = Math.floor((left + right) / 2);
        if (arr[left] > arr[mid]) {
            this.exchangeValue(left, mid, arr);
        } //确保mid 位置大

        if (arr[mid] > arr[right]) {
            this.exchangeValue(mid, right, arr);
            if (arr[left] > arr[mid]) {          //这里的思路不清晰，闹了错误，老师的那种写法感觉有问题
                this.exchangeValue(left, mid, arr);
            } //确保交换后的mid大
        } //确保right位大
        //mid放到right那个最大值的旁边：
        this.exchangeValue(mid,right-1,arr)
    }

分治过程的思路探究

我目前木有看老师怎么写的，我自己一下就钻进死胡同，写出来一个错误的复杂的逻辑了！
我需要拆解，复盘一下：

 _filter(left, right, arr) {
        if (right - 1 <= left) return;       //终结条件1，left,right相邻！
   //嗯，现在想想这里也要比较大小的
        let mid = Math.floor((left + right) / 2);  //中间数字 
        let nextLeft = left, nextRight = right;  //暂存初始的left,right，为了递归用！
        this.initMid(left, right, mid, arr);  //三个数字从小到大排列，然后中间的数跟right-1位置的数互换
        if (right - left === 2) return;  //这里的判断是假如left,mid,right就三个数，它们已经排好位了！
        right -= 2;  //这里的right位置去掉right，right-1，因为initMid的操作排位，mid也换到了right-1。
        const midVul = arr[nextRight - 1];
        while (left <= right) {  //终结点就是left = right，这里的等于会不会造成死循环？？
            if (left === right) {
                if (arr[left] > midVul) {
                  //这个结果是最好的结果，终结点的value正好大于枢纽的值，它两个互换就好了！
                    arr[nextRight - 1] = arr[left];
                    arr[left] = midVul;
                    this._filter(nextLeft, mid - 1, arr); 
                  //错了，nextRight的值根本就不应该是mid-1,应该是left-1，我知道哪里错了，后面的都错了！当时下午很困，竟然犯了这种低级错误！
                    this._filter(mid + 1, nextRight, arr);
                  //这里要不要加return? 加了return确实是不死循环了，但是问题来了，结果错了！
                  //先不看相等的时候的逻辑，先看不相等的时候的逻辑：
                } else if (arr[left] === midVul) {
                  //这个就是我贪心所为了，其实相等的情况，我也知道，不如直接当大于处理，或许少了很多的逻辑判断而更高效
                    const initMid = mid;//这里的逻辑错了！坑！
                    mid += 1;
                    while (arr[mid] === midVul) {
                        mid += 1;
                    }
                    if (mid + 1 < nextRight - 1) {
                        arr[nextRight - 1] = arr[mid + 1];
                        arr[mid + 1] = midVul;
                        this._filter(nextLeft, initMid - 1, arr);
                        this._filter(mid + 2, nextRight, arr);
                        //这里要不要加return?
                    } else {
                        this._filter(nextLeft, initMid - 1, arr);
                        this._filter(mid + 1, nextRight, arr);
                        //这里要不要加return?
                    }
                } else {
                    mid += 1;
                    const initMid = mid;
                    while (arr[mid] === midVul) {
                        mid += 1;
                    }
                    if (mid + 1 < nextRight - 1) {
                        arr[nextRight - 1] = arr[mid + 1];
                        arr[mid + 1] = midVul;
                        this._filter(nextLeft, initMid - 1, arr);
                        this._filter(mid + 2, nextRight, arr);
                        //这里要不要加return?
                    } else {
                        this._filter(nextLeft, initMid - 1, arr);
                        this._filter(mid + 1, nextRight, arr);
                        //这里要不要加return?
                    }
                }
            }
          //不相等的逻辑：我这里立马就是错的，应该跟相等的那里是互斥的情况：
            let min, max;
            while (!max && left < right) { //判断条件不该用!max,因为0！
                if (arr[left] > midVul) { 
                    max = arr[left];
                } else {
                    left++;
                }
            }
            while (!min && left < right) {//同上
                if (arr[right] < midVul) {
                    min = arr[left];
                } else {
                    right--;
                }
            }
            if (min !== undefined && max !== undefined) {
              //到了这里，我当时也有过感觉，如果判断min,max都不存在或者只有一个的情况的时候，
              //就是，right===left的时候，当时很后悔先写相等的时候的判断，太麻烦了！
                arr[right] = max
                arr[left] = min
                max = undefined
                min=undefined
                left++
                right--
            }//问题应该是出在上面的相等时候的判断那里了！
        }
    }

经过拆解复盘：我需要重新写一下，最优版本：

fastSort(){
  const {items} = this;
        this._filter(0, items.length - 1, items);
}
//改写了十多遍的成果，暂时测试了十多个31长度的随机数组成的数组通过了，，，妈妈屁！真恶心：
建议看后面的老师的写法！因为可能有一个bug我还没解决，，，
_filter(left, right, arr) {
        //判断left === right ,left+1=right;right-2 = left的情况：
        if (left === right) return;
        if (left + 1 === right) {
            if (arr[left] > arr[right]) {
                this.exchangeValue(left, right, arr);
            }
            return;
        }
        //找到枢纽，并排序三个数字，交换位置，最后枢纽再交换位置到right-1那！
        this.initMid(left, right, arr);

        //如果left+2=left，这时候就可以返回了：
        if (left + 2 === right) return;

        //记录初始的left,right,midValue
        const nextLeft = left, nextRight = right, midV = arr[right - 1];
        //枢纽初始化后，占位right-1，right要变
        console.log(left,right,'start',arr);

        right -= 2;

        //这时候开始正式的差分遍历，交换了：
        while (left <= right) {
            let min, max;
            //从做开始寻找大于midV的值，直到找到，或者直到right的位置
            while (max === undefined && left <= right) {
                if (arr[left] > midV) {
                    max = left;
                } else {
                    //这里需要判断，假如left=== right的时候：下面没必要了：
                    if (left === right) {
                        if (max) {
                            this.exchangeValue(left, nextRight - 1, arr);
                            return right - 1 > nextLeft &&
                                this._filter(nextLeft, right - 1,arr);
                        } else {
                            return this._filter(nextLeft, nextRight - 2,arr);
                        }
                    }else{
                        left < right && left++;
                    };
                }
            }

            console.log(left, right, arr, midV, "max");
            //从右开始，寻找小于midV的位置：
            while (min === undefined && left <= right) {
                if (arr[right] < midV) {
                    min = right;
                } else {
                    //这里需要判断，假如left=== right的时候：
                    //分析了一下，left===right的时候，只能有一个min或者max有值，而max可以有值，min无法有值：
                    if (left === right) {
                        if (max !== undefined) {
                            this.exchangeValue(max, nextRight - 1, arr);
                            console.log(max,'max',nextRight-1);
                            max - 1 > nextLeft &&
                            this._filter(nextLeft, max - 1, arr);
                            return nextRight > max + 1 &&
                                this._filter(max + 1, nextRight, arr);
                        } else {
                            //没可能
                        }
                    }else{
                        left < right && right--;
                    }
                }
            }
            //max,min都存在的时候
            this.exchangeValue(max, min, arr);
            if (left + 1 === right) {
                this.exchangeValue(right, nextRight - 1, arr);
                this._filter(nextLeft, left, arr);
                return nextRight > right + 1 &&
                    this._filter(right + 1, nextRight, arr);
            } else {
                left++;
                right++;
            }
        }
    }

终极代码：看了老师的思路，重新改进控制思路

        _fastSort(left, right, arr) {
        console.log(right,left,'start0');
        if (left >= right) return;
        if (left + 1 === right) {
            if (arr[left] > arr[right]) {
                this.exchangeValue(left, right, arr);
            }
            return;
        }
        this.initMid(left, right, arr);
        if (left + 2 === right) return;
        const nextLeft = left, nextRight = right, midV = arr[right - 1];
        right -= 2;
        left++;
        console.log(right,left,'start1');
        while (left < right) {
            let min, max;
            while (max === undefined && left < right) {
                if (arr[left] > midV) {
                    max = left;
                } else {
                    left++;
                }
            }
            while (min === undefined && left < right) {
                if (arr[right] < midV) {
                    min = right;
                } else {
                    right--;
                }
            }
            if (min && max) {
                this.exchangeValue(min, max, arr);
                left++;
                right--;
            }
            console.log(arr,'内',min,max,midV);
        }
        console.log(arr,'外',left,right);
        if (left === right) {
            if (arr[left]>midV){
                this.exchangeValue(left, nextRight - 1,arr);
                this._fastSort(nextLeft, left - 1, arr);
                this._fastSort(left + 1, nextRight, arr);
            }else {
                if (left+1===right-1){
                    this._fastSort(nextLeft,left,arr)
                }else{
                    this.exchangeValue(left+1, nextRight - 1,arr);
                    this._fastSort(nextLeft, left , arr);
                    this._fastSort(left + 2, nextRight, arr);
                }
            }
        }else{
            this.exchangeValue(left, nextRight - 1,arr);
            this._fastSort(nextLeft, left - 1, arr);
            this._fastSort(left + 1, nextRight, arr);
        }
    }

        fastSort1() {
        const {items} = this;
        this._fastSort(0, items.length - 1, items);
    }

因为前天太困了，看老师在如何筛选的时候的过程时，都是半看半推，给自己下限制了，，，教训！
为什么自己喜欢演绎法？？？
向上一个维度的状态管理，之前的方法也就很容易写出来了！
老师视频里的方法是错的！
复杂在我把left===right的情况强行纳入掌控了，做拦截，结果真麻烦！
当初一开始写的时候，我却是想过要不要独立出去，，，哎！教训！不该秀自己的才智，挑战。耽误太多时间了！
当然，全靠自己深耕云了，现在写简单写法思路很快的。

终极代码第二版

const exchange = (ind1,ind2,arr)=>{
  const v = arr[ind1]
  arr[ind1] = arr[ind2]
  arr[ind2] = v
}

const sort = (left,right,arr)=>{
  if(left>=right)return;
  if(left+1===right){
    if(arr[left]>arr[right]){
      exchange(left,right,arr)
    }
    return;
  }
  const mid = Math.floor((left+right)/2)
  if(arr[left]>arr[mid]){
    exchange(left,mid,arr)
  }
  if(arr[mid]>arr[right]){
    exchange(mid,right,arr)
    if(arr[left]>arr[mid]){
      exchange(left,mid,arr)
    }
  }
  if(left+2===right) return;
  exchange(mid,right-1,arr)
  const nextLeft = left,nextRight=right,midV=arr[right-1]
  left++
  right-=2
  while(left<right){
    let min,max
    while(max===undefined&&left<right){
      if(arr[left]>midV){
        max=left
      }else{
        left++
      }
    }
    while(min===undefined&&left<right){
      if(arr[right]<midV){
        min=right
      }else{
        right--
      }
    }
    if(min&&max){
      exchange(min,max,arr)
      left++
      right--
    }
  }
 //主要是对这里进行复盘！！！！！
  昨晚太晚了，就只想穷举法，所以思路不清晰，还有就是也不熟练，
  今天自己一遍手写出了个bug，自己觉得就是这里出问题了，left,right参数一定要认真传不要马虎！
  还有，系统地分析跳出循环后的left,right的场景，才是掌握的根本：
  昨晚先划分了left===right的还有大于的情况，等于的里面又划分了arr[left]大于或小于midV的情况
  还有极限倒霉的情况arr[left]小于的情况下，left+1===nextRight-1的情况。



  今天再仔细分析：
  不管left大于还是等于,都要看arr[left]的值跟midV作比较，所以最外层不需要！
  主逻辑：arr[left]比较midV:
  大于的话很简单！
  小于的话：看left+1位是不是等于nextRight-1，等于就是那种极端情况，不等于就是另一种情况。
    if(arr[left]>midV){
             exchange(left,nextRight-1,arr)
            sort(nextLeft,left-1,arr)
            sort(left+1,nextRight,arr)
    }else{
      if(left+1===nextRight-1){
        sort(nextLeft,left,arr)
      }else{
            exchange(left+1,nextRight-1,arr)
            sort(nextLeft,left,arr)
            sort(left+2,nextRight,arr)
      } 
    }
  return arr
}
const arr  = []
for(let i=0;i<=30;i++){
  arr.push(Math.floor(Math.random()*100))
}
console.log(sort(0,arr.length-1,arr))

效率

迄今为止最快的平均速度的排序算法！