引出

截屏2020-04-11 下午5.24.11.png

研究事物之间的关系，通过点与线具现化的感觉。抽象的关系，实体表现出来！

示例

截屏2020-04-11 下午5.45.15.png

人与人之间的联系性！

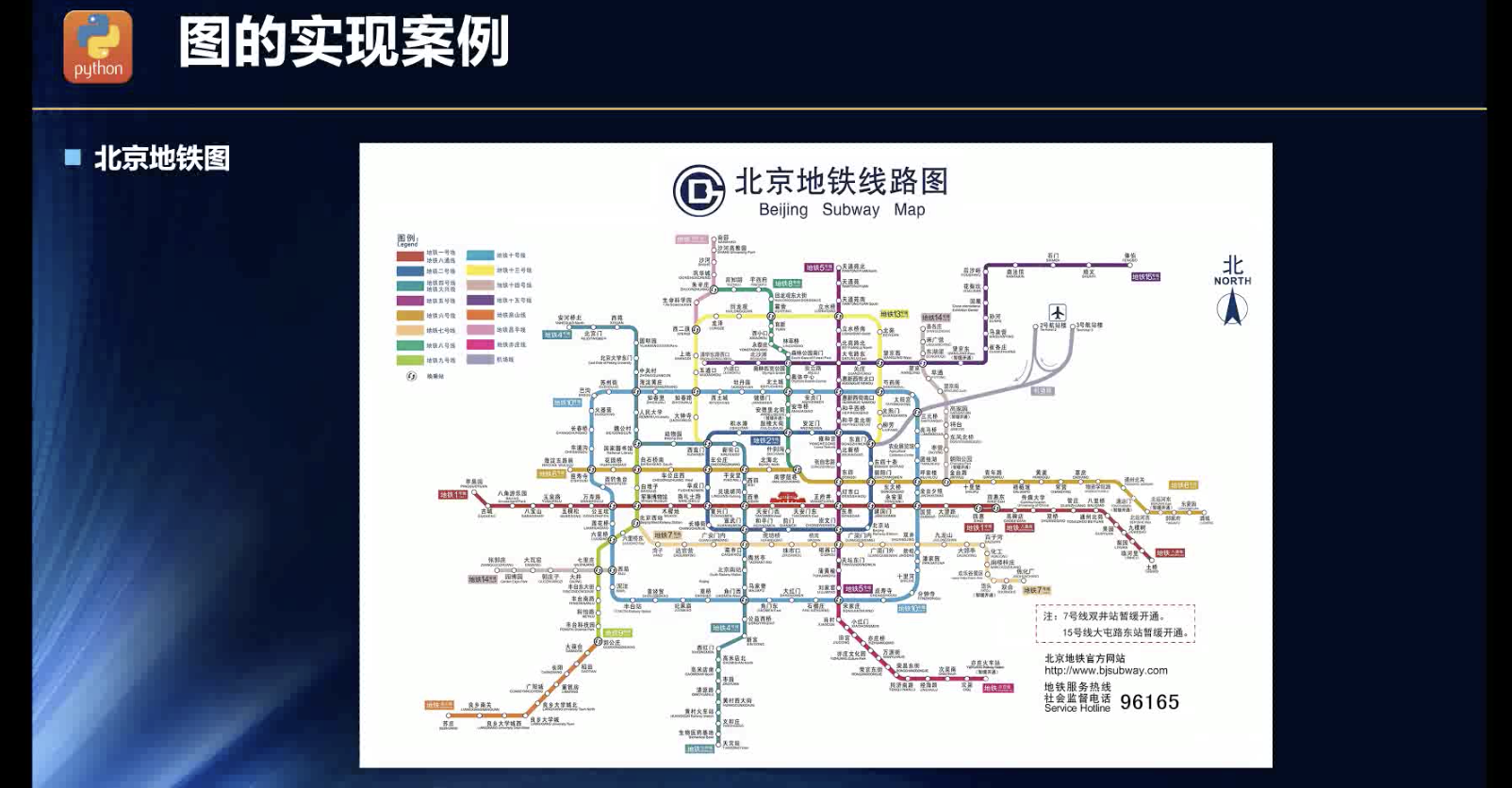
截屏2020-04-11 下午5.45.56.png

交通网络图，节点与节点之间的联系！

截屏2020-04-11 下午5.46.45.png

图结构的概念

图结构：顶点，连线！二叉树太讲究顺序，两个点之间有因果关系，主副。图结构更大的范畴了，图的顶点互相之间独立存在的！

截屏2020-04-11 下午5.51.00.png

七桥问题

截屏2020-04-11 下午6.10.38.png

图论的由来。

截屏2020-04-11 下午6.11.18.png

老师对抽象的理解也是可以的，这两天做递归算法的时候，就觉得把现实问题抽象转化是为了想要用数学知识简化问题 的。同样的还有一种逆向，就是把抽象的一些逻辑简单具象化，也比较重要的。尤其是算法题目的意思有木有明白彻底！

术语

截屏2020-04-12 下午11.06.33.png

点与边！

截屏2020-04-12 下午11.17.07.png

边的意义！路径概念！增加属性！

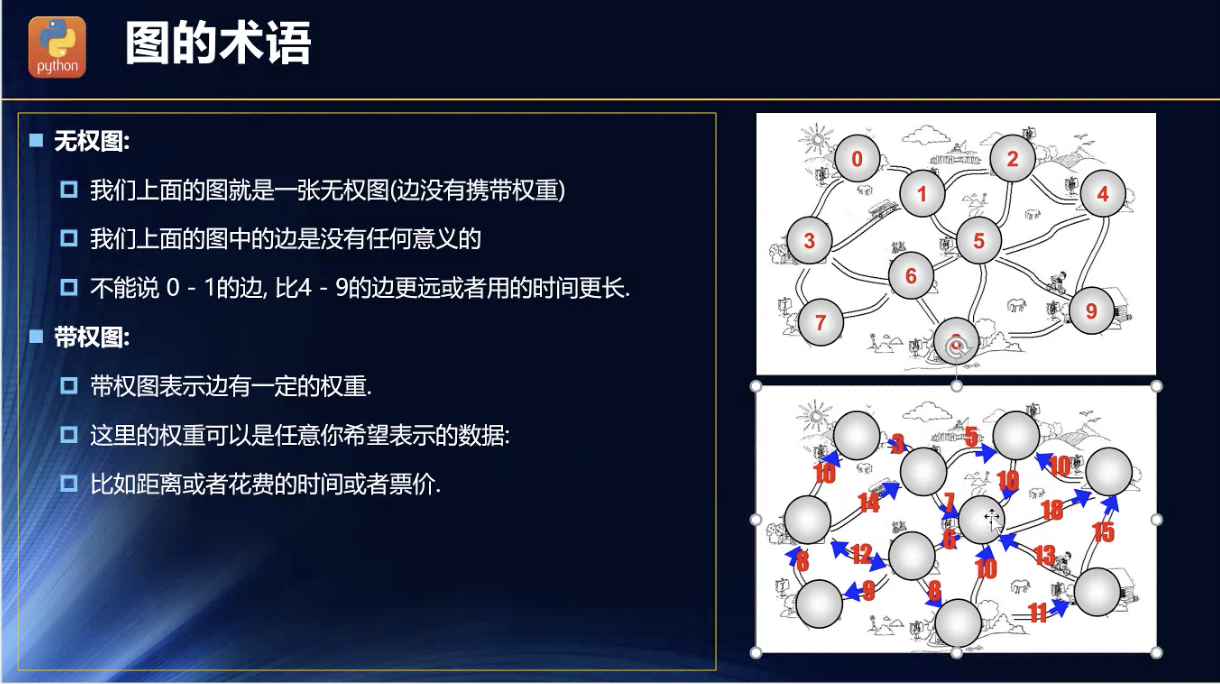
截屏2020-04-12 下午11.18.07.png

加属性：权重！

图的表示

截屏2020-04-13 上午12.26.08.png

上面说过图跟树的关系，树属于图，但是树太片面了，规则局限很明显的，有因果：父子关系。而图的每个顶点默认的都是相互独立的，不讲究插入顺序而导致的节点之间的关系发生变化的。
所以，各个顶点是相互独立的，就适合用数组来存储了！

邻接矩阵

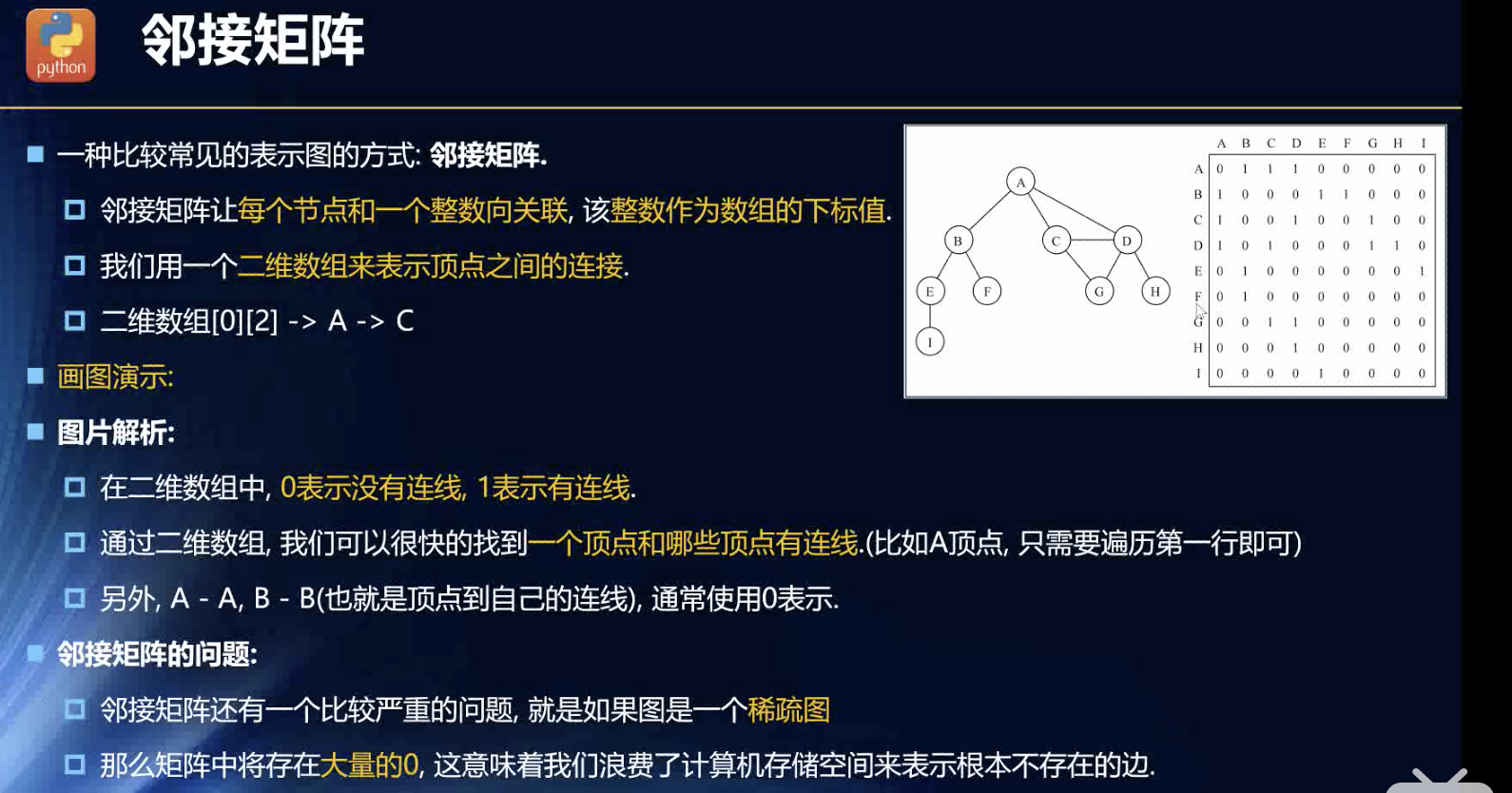
截屏2020-04-13 上午12.29.28.png

看着挺眼熟的，其实就是关系型数据库里的主键表与副键表的模拟了！
二维数组是个知识点的，而且存储的数值，可提前约定好，数值也可以多用，指代权重等。
缺点就是多个点的简单的路径关系，会浪费内存空间，我觉得适合成熟的网型现象！

邻接表

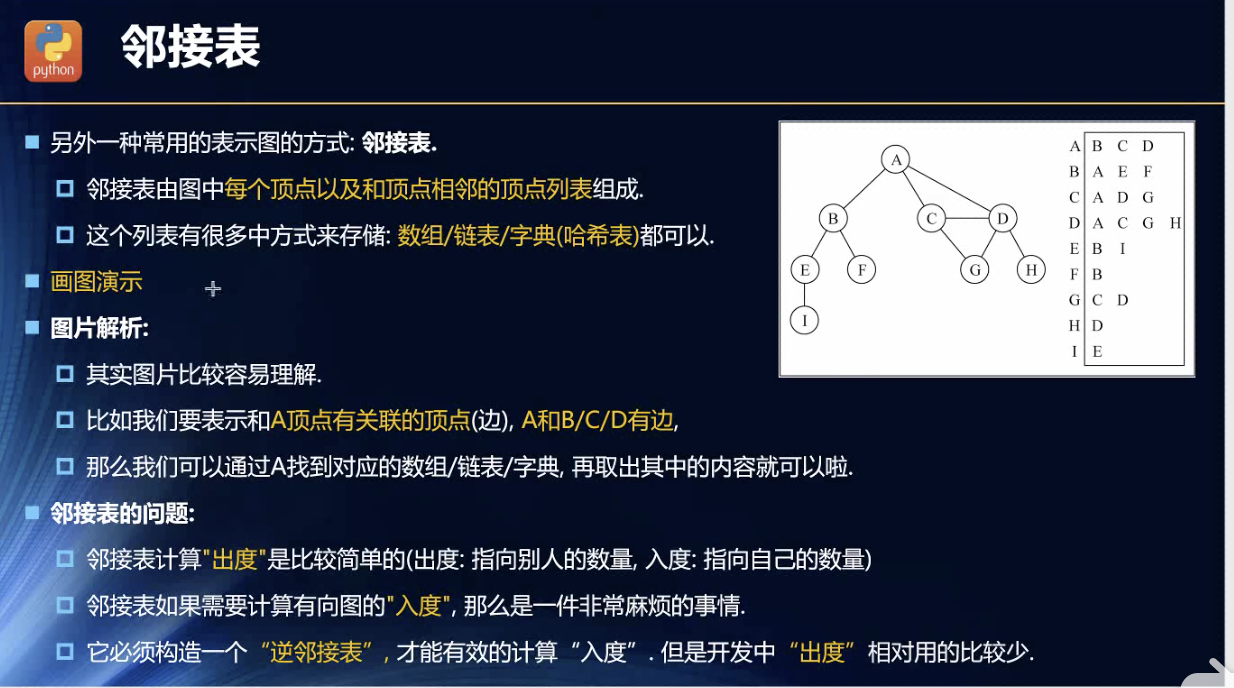
截屏2020-04-13 上午11.13.09.png

ppt有错误！ 是入度用的少！所以，邻接表比较常用！
其实很像哈希表的数组形式存储重复数据的结构！这里其实就是个字典。主键是key，对应一个表数据。

封装

  1. //图封装：邻接表
  3. const {Queue1} = require("./queue");
  4. const {Dictionary} = require("./dictionary");
  7. class Graph {
  8.     constructor(vertexes = []) {
  9.         this.vertexes = vertexes;
  10.         let obj = {}, obj1 = {};
  11.         if (vertexes.length) {
  12.             vertexes.map(
  13.                 key => (obj[key] = []) && (obj1[key] = 1)
  14.             );
  15.         }
  16.         this.edges = new Dictionary(obj);
  17.         this.vertexState = obj1;
  18.         this.queue = new Queue1();
  19.     }
  21.     hasVertex(v) {
  22.         return this.vertexes.indexOf(v) >= 0;
  23.     }
  25.     addVertex(v) {
  26.         if (!this.hasVertex(v)) return false;
  27.         this.vertexes.push(v);
  28.         this.edges[v] = [];
  29.         this.vertexState[v] = 1;
  30.         return true;
  31.     }
  33.     addEdge(v, v1, unidirectional) {
  34.         if (!this.hasVertex(v) || !this.hasVertex(v1)) return false;
  35.         const edges1 = this.edges.get(v), edges2 = this.edges.get(v1);
  36.         if (edges1.indexOf(v1) < 0) {
  37.             edges1.push(v1);
  38.         }
  39.         if (!unidirectional && edges2.indexOf(v) < 0) {
  40.             edges2.push(v);
  41.         }
  42.         // console.log(edges2,edges1);
  43.         return true;
  44.     }
  46.     bfs(start, callback) {
  47.         callback && callback(start);
  48.         this.vertexState[start] = 2;
  49.         this.queue.enqueue(start);
  50.         this._bfs(start, callback);
  51.         this.initStates();
  52.     }
  54.     initStates() {
  55.         Object.keys(this.vertexState).map(
  56.             k => this.vertexState[k] = 1
  57.         );
  58.     }
  60.     _bfs(start, callback) {
  61.         //1代表未被访问，2代表访问所有的关联未完成，3代表所有的关联都访问完了
  62.         //callback && callback(start)
  63.         //this.vertexState[start] = 2
  64.         // console.log(999,start);
  66.         const edges = this.edges.get(start);
  68.         edges.map(
  69.             (key, ind) => {
  70.                 if (this.vertexState[key] === 1) {
  71.                     callback && callback(key);
  72.                     this.vertexState[key] = 2;
  73.                     this.queue.enqueue(key);
  74.                 }
  75.             }
  76.         );
  77.         this.vertexState[start] = 3;
  78.         this.queue.dequeue(start);
  79.         // console.log(this.queue,this.vertexState,999);
  80.         while (this.queue.size()) {
  81.             this._bfs(this.queue.front().data, callback);
  82.         }
  83.     }
  85.     dfs(start, callback) {
  86.         this.stack = [];
  87.         this._dfs(start, callback);
  88.         this.stack = null;
  89.         this.initStates();
  90.     }
  92.     _dfs(start, callback) {
  93.         const {stack} = this;
  94.         if (this.vertexState[start] === 1) {
  95.             // console.log("ccc");
  96.             callback && callback(start);
  97.             this.vertexState[start] = 2;
  98.             stack.push(start);
  99.         }
  100.         const edges = this.edges.get(start);
  101.         // console.log(edges,'ee',start);
  102.         const next = edges.length && edges
  103.             .find(k => this.vertexState[k] === 1);
  104.         // console.log(stack,'s',next);
  106.         if (next) {
  107.             this._dfs(next, callback);
  108.         } else {
  109.             this.vertexState[start] = 3;
  110.             stack.pop();
  111.             if (stack.length) {
  112.                 this._dfs(stack[stack.length - 1], callback);
  113.             }
  114.         }
  116.     }
  118.     toString() {
  119.         return this.vertexes.reduce(
  120.             (a, b) =>
  121.                 a + (a ? "\n" : "") + `${b} -> ${this.edges.get(b).join(" ")}`
  122.             , ""
  123.         );
  124.     }
  125. }
  127. const graph = new Graph(
  128.     ["a", "b", "c", "d", "e", "f", "g", "h", "i"]);
  130. graph.addEdge("a", "b");
  131. graph.addEdge("a", "c");
  132. graph.addEdge("a", "d");
  133. graph.addEdge("c", "d");
  134. graph.addEdge("c", "g");
  135. graph.addEdge("d", "g");
  136. graph.addEdge("d", "h");
  137. graph.addEdge("b", "e");
  138. graph.addEdge("b", "f");
  139. graph.addEdge("e", "i");
  140. graph.bfs("a", v => console.log(v));
  141. console.log(9);
  142. graph.dfs("a", v => console.log(v));
  143. // console.log(graph);

图的遍历：广度优先、深度优先

截屏2020-04-13 下午11.30.20.png

演绎法得出的，其实广度优先比较硬解题的意思了，按层级遍历的，不重不漏很容易的。
而深度优先的算法，比较注意细节了，倾向于走到一条路的头之后再往回走到之前的节点，看看有木有岔路，有岔路就进去走到头，再回来，回去的路上遇到岔路就进去，如此重复，就是递归了。

状态管理

这里会有疑惑，节点需要区分，访问过没访问过，分支访问探索完了？这里就有了状态意识了！

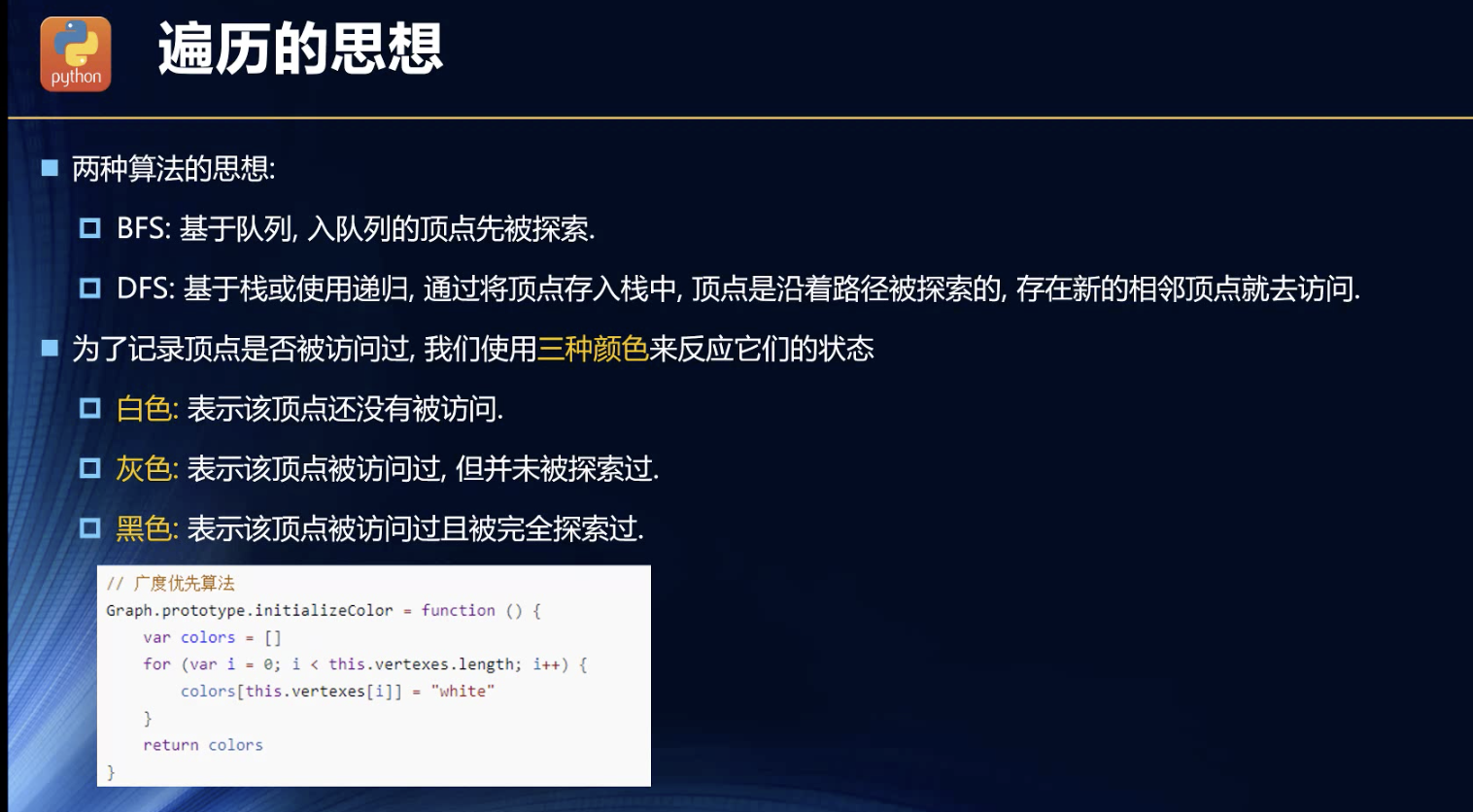
截屏2020-04-14 上午10.46.28.png

广度优先搜索

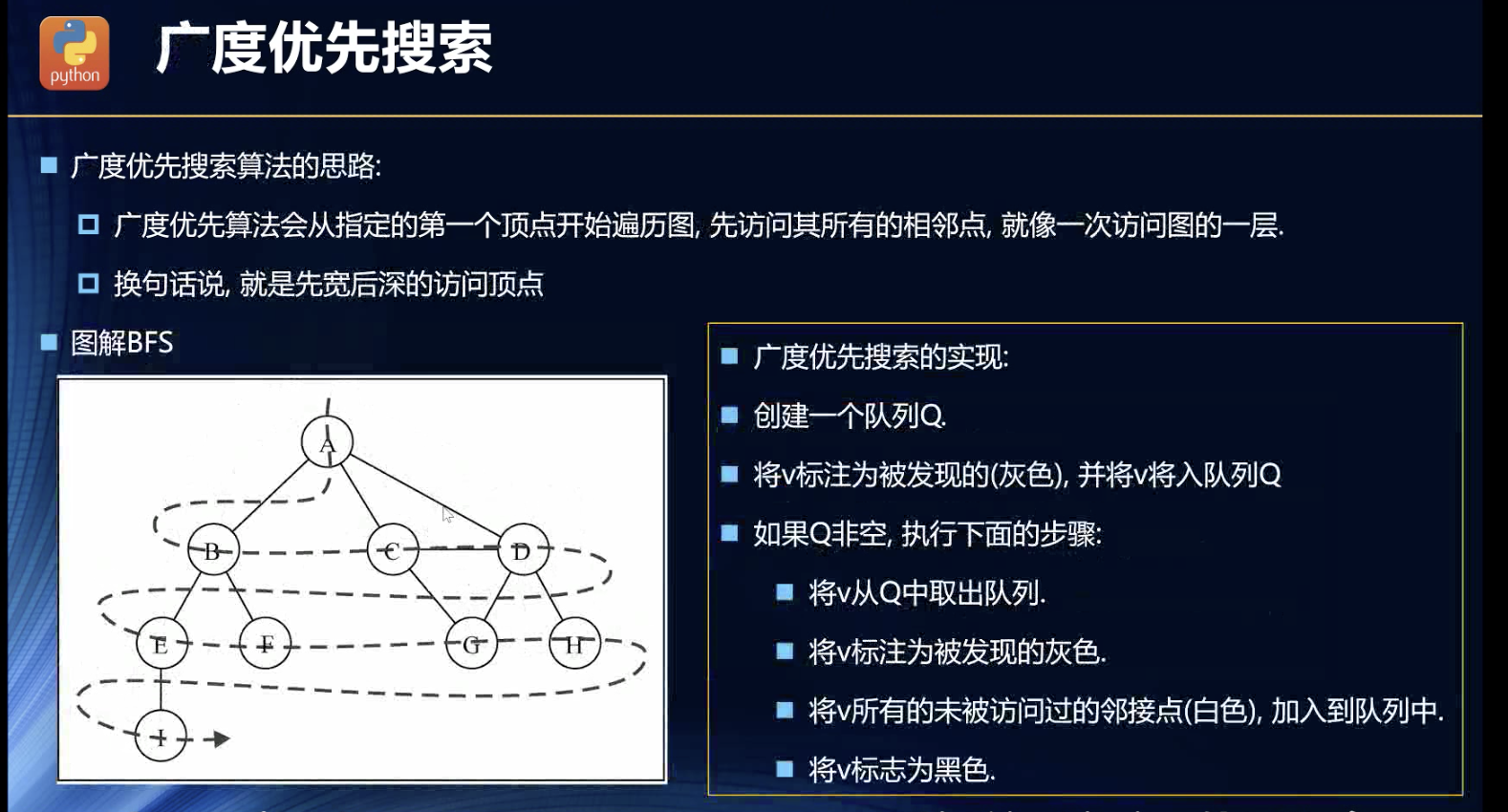
截屏2020-04-14 下午4.05.25.png

我一开始自己做的时候，没用队列。通过筛选出来所有的顶点的state为2的，遍历它们，进行后续。每一层的变量，多一次筛选。虽然做出来了，但是确实是队列比较好的。
我尝试不用队列，每层的遍历添加了一个数组来存储产生的state为2的顶点。但是失败了！我反复思考，发现是这个问题的：

  1.          bfs(start,callback){
  2.         callback && callback(start)
  3.         //1代表未被访问，2代表访问所有的关联未完成，3代表所有的关联都访问完了
  4.         this.vertexState[start] = 2
  5.         this.queue = [start]   //这里存储
  7.         this._bfs(start,callback)
  8.         Object.keys(this.vertexState).map(
  9.             k=>this.vertexState[k]=1
  10.         )
  11.     }
  13.     _bfs(start,callback){
  14.         //callback && callback(start)
  15.         //this.vertexState[start] = 2
  16.         // console.log(999,start);
  18.         const edges = this.edges.get(start)
  20.         edges.map(
  21.             (key,ind)=>{
  22.                 if (this.vertexState[key] === 1){
  23.                     callback && callback(key)
  24.                     this.vertexState[key] = 2   //修改状态
  25.                     this.queue.push(key)   //添加新的2状态的点,这里有问题
  26.                 }
  27.             }
  28.         )
  29.         this.vertexState[start] = 3    //完结了，把start的顶点标为完成
  30.         this.queue.shift()     //删除完成的点
  31.         // console.log(this.queue,this.vertexState,999);
  33.           //这里我用的是遍历：这里也错了,其实可以用while循环，强制一个执行完了再执行，
  34.       //而不是map循环，无法控制。因为假如现在正在循环第二层的b，执行到上面的 this.queue.push(i)，
  35.       //this.queue.map的表现是，动态的，直接把i也放入跟b同一层进行遍历了，而不是下一层。
  36.           this.queue.map(
  37.           k=>{
  38.               this._bfs(k,callback)
  39.           }
  40.         )
  41.     }

不过，我后来，自己重新改了一下原本用数组做出来的队列的封装，我思量到底是用双链表还是单链表做？选了双链表。然后用了实在的队列进行解题，发现效果是真的好的不得了！

        //1代表未被访问，2代表访问所有的关联未完成，3代表所有的关联都访问完了
         bfs(start,callback){
        callback && callback(start)
        this.vertexState[start] = 2
        this.queue.enqueue(start)   //这是双链表实现的队列，暂时没有优先队列这一特点。

        this._bfs(start,callback)
        Object.keys(this.vertexState).map(
            k=>this.vertexState[k]=1
        )
    }

    _bfs(start,callback){
        //callback && callback(start)
        //this.vertexState[start] = 2
        // console.log(999,start);

        const edges = this.edges.get(start)

        edges.map(
            (key,ind)=>{
                if (this.vertexState[key] === 1){
                    callback && callback(key)
                    this.vertexState[key] = 2
                    this.queue.enqueue(key)
                }
            }
        )
        this.vertexState[start] = 3
        this.queue.dequeue(start)
        // console.log(this.queue,this.vertexState,999);
        while (this.queue.size()){
            this._bfs(this.queue.front().data,callback)
        }
    }

深度优先搜索

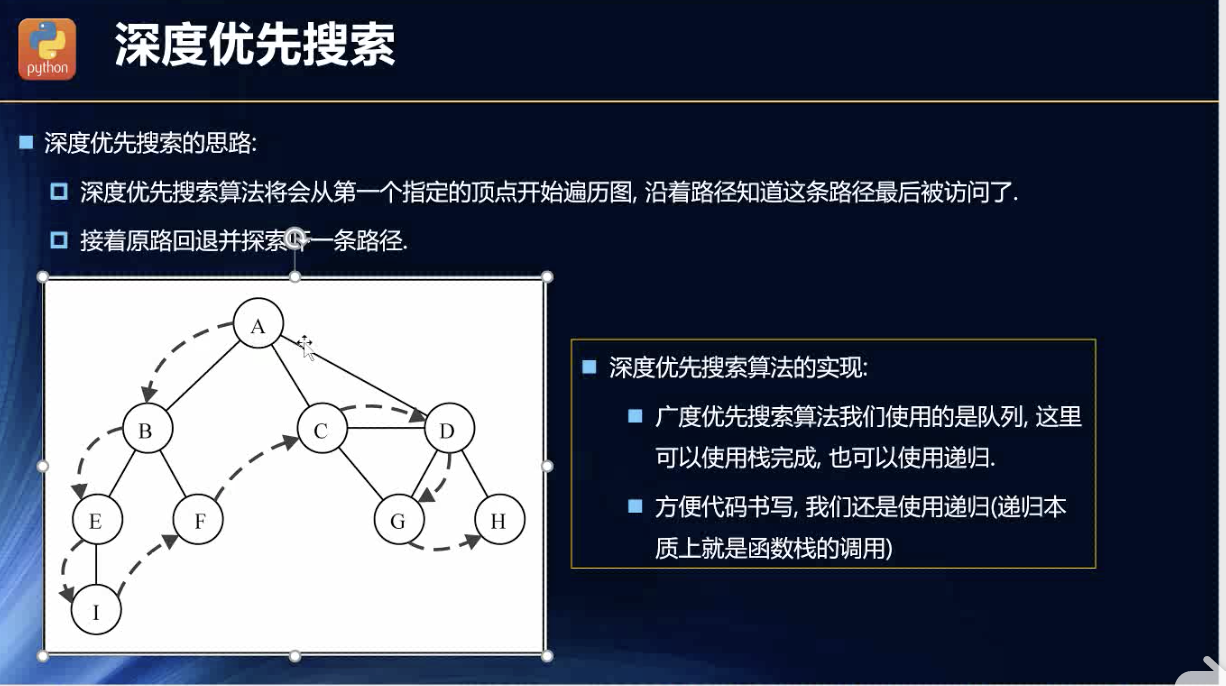
截屏2020-04-14 下午6.33.21.png

深度优先算法，我演绎了一下，发现很适合用栈的逻辑去应对的。木有看老师的视频，然后完全模拟了栈的思路：
这样完全模拟，在我看到老师的写法之后，发现自己变笨了！
先看：

         dfs(start, callback) {
        this.stack = [];  //栈
        this._dfs(start, callback);
        this.stack = null;
        this.initStates();
    }

    _dfs(start, callback) {
        const {stack} = this;
        if (this.vertexState[start] === 1) {
            // console.log("ccc");
            callback && callback(start);
            this.vertexState[start] = 2;
            stack.push(start);   //入栈
        }
        const edges = this.edges.get(start);
        // console.log(edges,'ee',start);
        const next = edges.length && edges
            .find(k => this.vertexState[k] === 1);
        // console.log(stack,'s',next);

        if (next) {
            this._dfs(next, callback);  //重复
        } else {
            this.vertexState[start] = 3;
            stack.pop();  //到栈顶了，出栈
            if (stack.length) {
                this._dfs(stack[stack.length - 1], callback); //新的重复
            }
        }
    }

而老师的栈的思想，其实就是遍历中递归，很简单的套路！

         dfs1(start, callback) {
        if (this.vertexState[start] === 1) {
            callback && callback(start);
            this.vertexState[start] = 2;
        }
        this.edges.get(start).map(
            k => {
                if (this.vertexState[k] === 1) {
                    this.dfs1(k, callback);
                }
            }
        );
              this.initStates();
    }

又对栈加深了印象了！今天的队列和栈真的是帮大忙了！