红黑树

开篇老师只是说很难！

我前面的推导，如何实现平衡二叉树，我也是构思了一下，确实是很木得头绪，因为涉及到了微调的。

理论

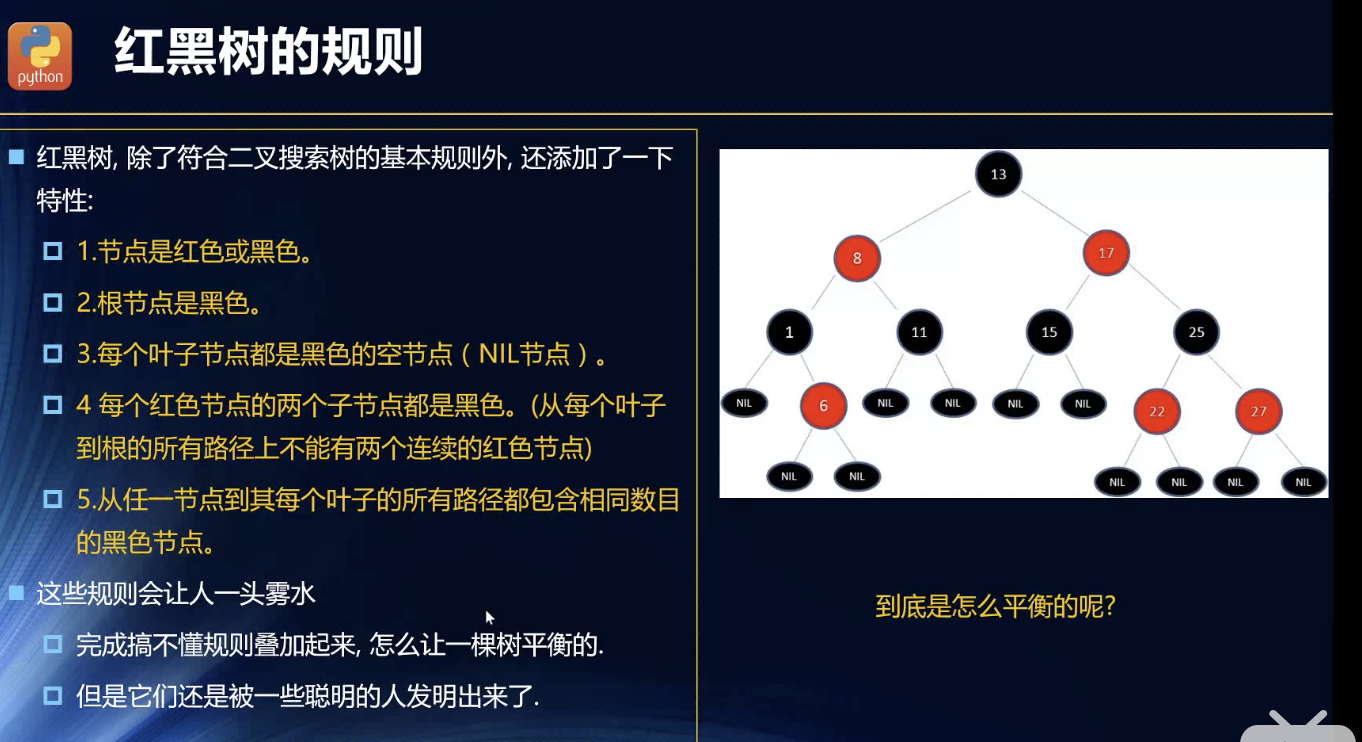
规则

分析

我上篇在推导的时候，比较倾向于，一个三角形去看数据，顶点总是middle大小的值。而分布均匀的意思，本来就是尽可能地组成多个三角形的嵌套的意思。好比：记录下当前插入的值，下一个值比它小点，第二个值比它大点。然后更新记录的值为small和large的值。下次再插入，重复如此操作。
从数学角度去想，理想的结果——
其实根节点很简单，就是目前所有节点的大小排序后的中间位置的值。
而把整个树压缩下拉看：

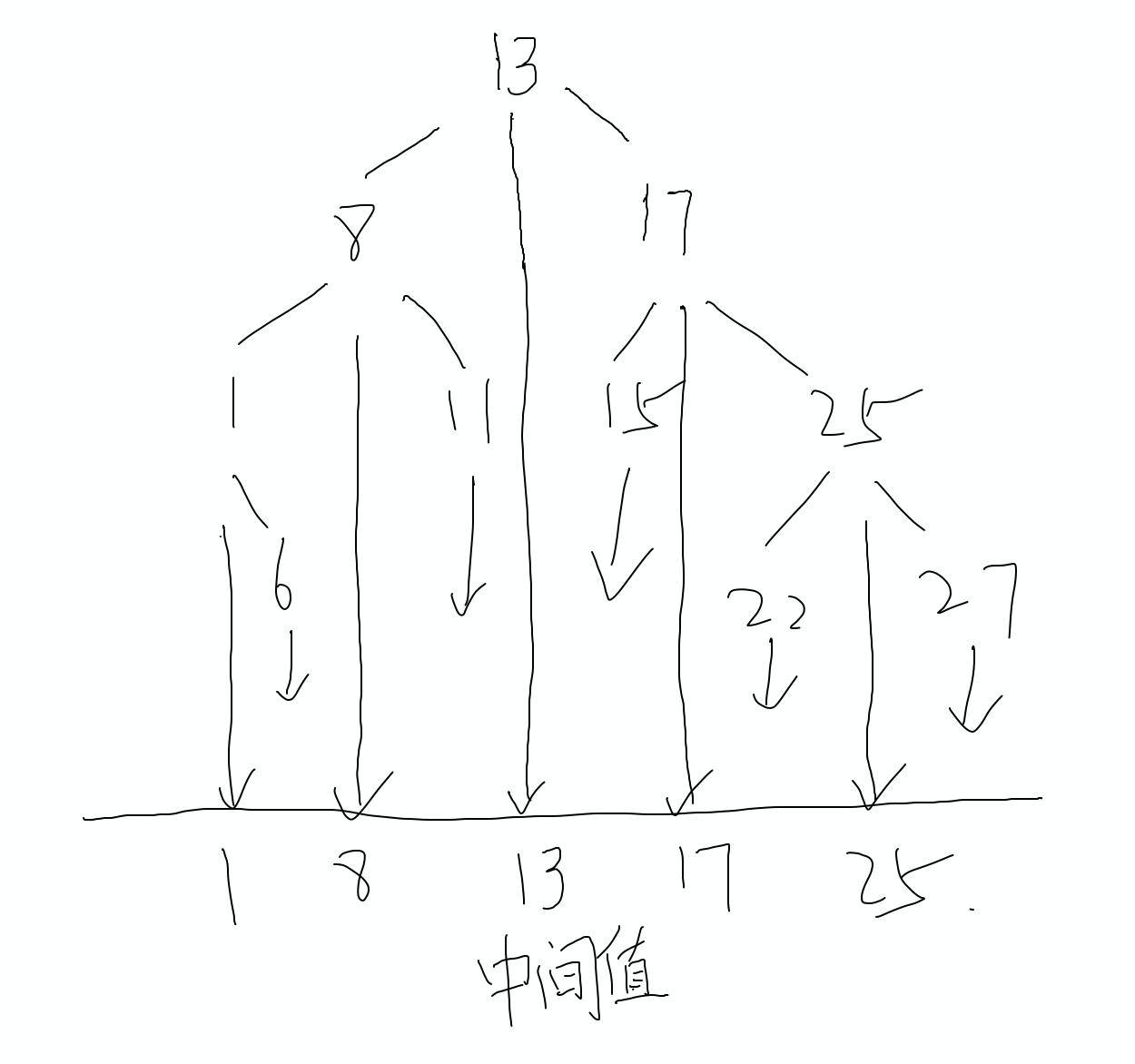
意思就是从大到小排列后，跳过紧挨着的插入下一个，再回头插入紧挨着的。
顶点总是左右子节点的中间值大小。
左右子节点总是跟中间值隔着一个值。

这是我的最理想状态的构建了。如何跟红黑挂钩？？？

如果中间值13为黑，相邻的11，15为黑，8就为红，6为红，1为黑。黑红间隔开，除了根节点紧挨着的两个数都是黑。
这算是一种标记了，现在如果我要插入4：

原： [1 ,6 ,8 ,11 ,13 ,17 ,22 ,25 ,27]
对应 黑  红  红  黑  黑  黑  红   红  黑
现在：[1 , 4 , 6 ,    8 ,11 ,13 ,17 ,22 ,25 ,27]
            红     黑    红   红  黑  黑  黑   红  红   黑

这，，，暂时木有推导啥。算了，拿来主义了！

红黑树的相对平衡

比较玄之又玄，什么意思？就是用已知的特征来证明了。关键的特征：
不相连的红节点，没问题！
所有的路径都有相同是黑节点？？
奥，我可能钻牛角尖了，或许这是实现出来的规则罢了！那就有个问题了，为啥要有这样的规则？原来是为了保证这里的？？？有些懂了，先如此理解吧！

为了保证树里的最短路径跟最长路径相差不大，做了这样的设定，所有的路径的黑节点一样多！

变色

插入一个节点，这个节点是红色还是黑色？？
老师的意思是红色是默认色！在我看来，是红色还是黑色都可能会引起冲突的！
先考虑加进去的位置是哪里的！这部分符合一般的二叉树的插入逻辑。定好位之后，就进行判断了，要满足红黑树的那几个特征：
红红色不可连续出现！这里可能会导致变色了！
所有的路径的黑色节点数目相等！这个最麻烦了！

旋转

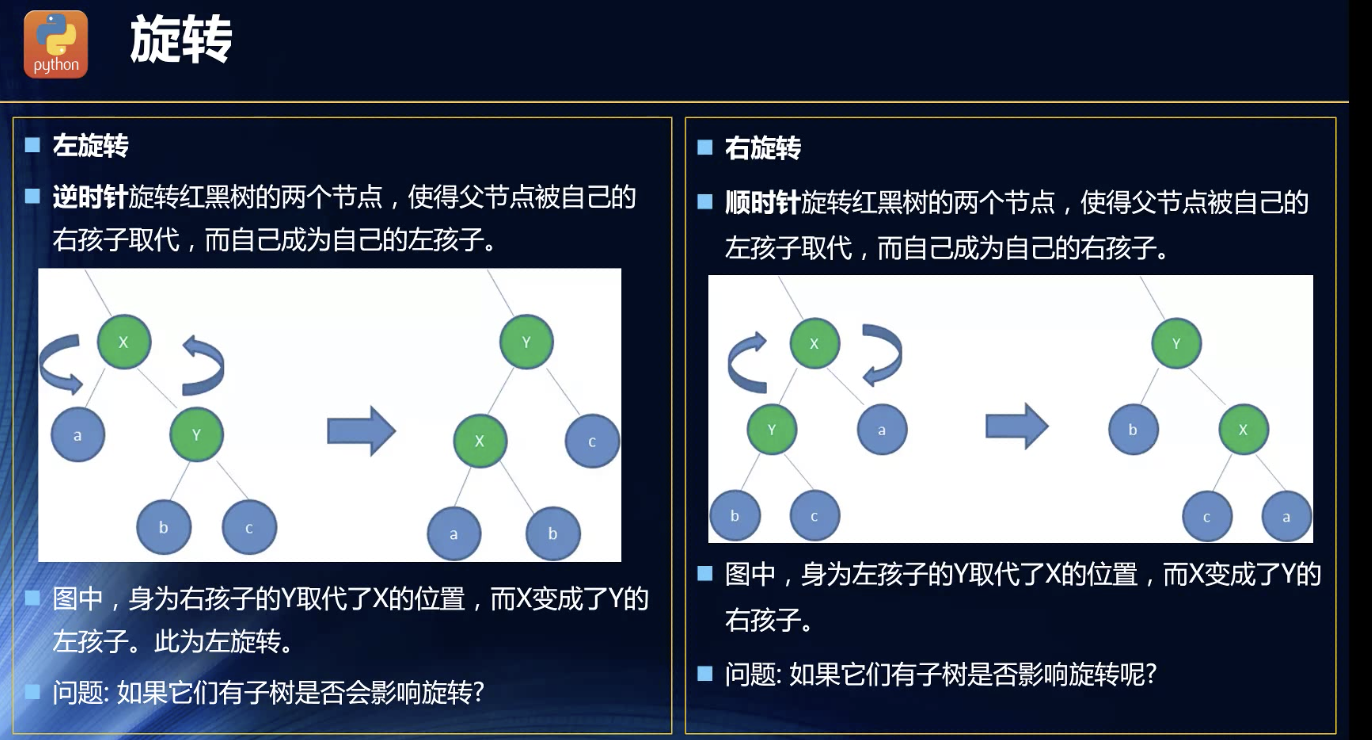
套路变色上面已经说过了，现在学的是三种套路！为什么要如此？我想到了前面推导的时候，说过的微调。但是我还是无法明白，不修改根节点，很难实现上面提到过的完美模型结果，用中间值做根节点，间隔插入。
。。。我突然觉得为什么旋转了？
**

旋转就是微调！坐旋转就是向左边减一个节点，右边加一个节点！右旋转同理！

此处要有掌声！我很牛皮啊！淡定，，，创造红黑树的人，真的是太聪明了！

这里老师主要讲的是套路了，就不多解释了！

我觉得红黑树有大用！尤其是在一些平衡问题，微调控制的场景中！

插入分析

插入根节点和插入到黑色节点的left/right

根节点不用说了！
插入到黑色节点的left/right。为啥随意了？因为新节点是红色的，黑节点的数量在路径上没改动的，只是红节点多了一个。

插入的节点位置的父节点以及父节点的兄弟节点的颜色为红

因为默认插入的节点的颜色为红。连续出现红节点就不符合规则了。

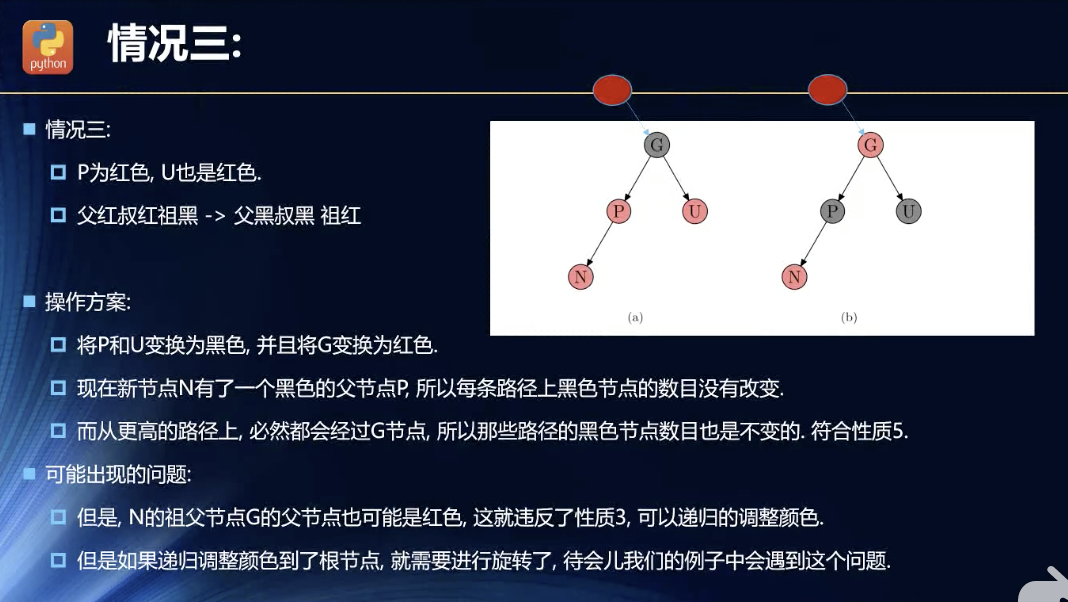
规则是：逐层变色。递归。直到根节点那里造成了冲突，就用旋转。

插入的节点位置是红色父节点的左节点，同时父节点的兄弟节点为黑色

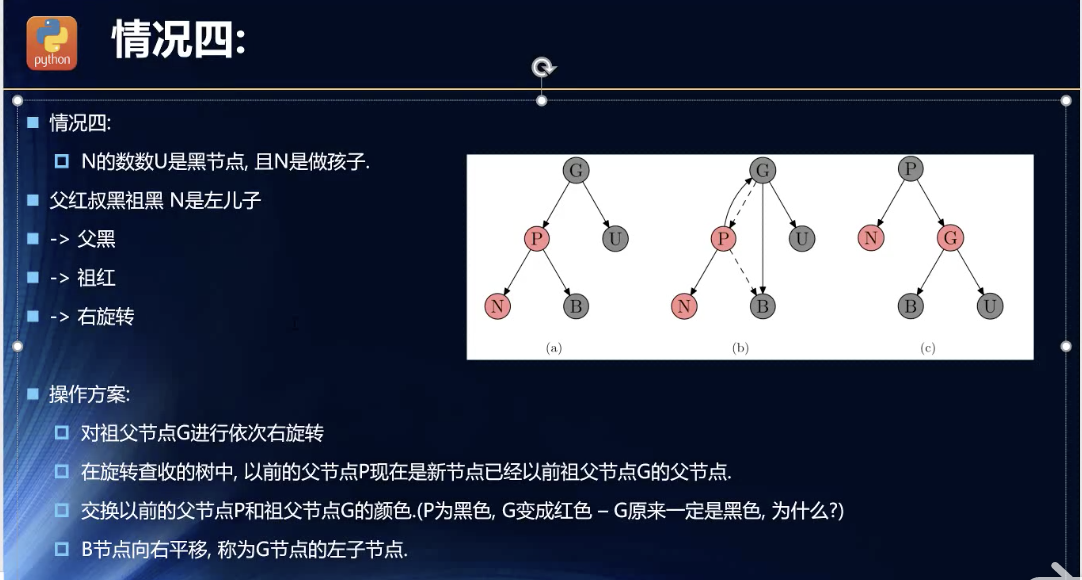
上次的是父节点，叔叔节点都是红色的，没办法仅仅通过变色实现。这次的情形，则是对右旋转的一种实现！

插入的节点位置是红色父节点的右节点，同时父节点的兄弟节点为黑色

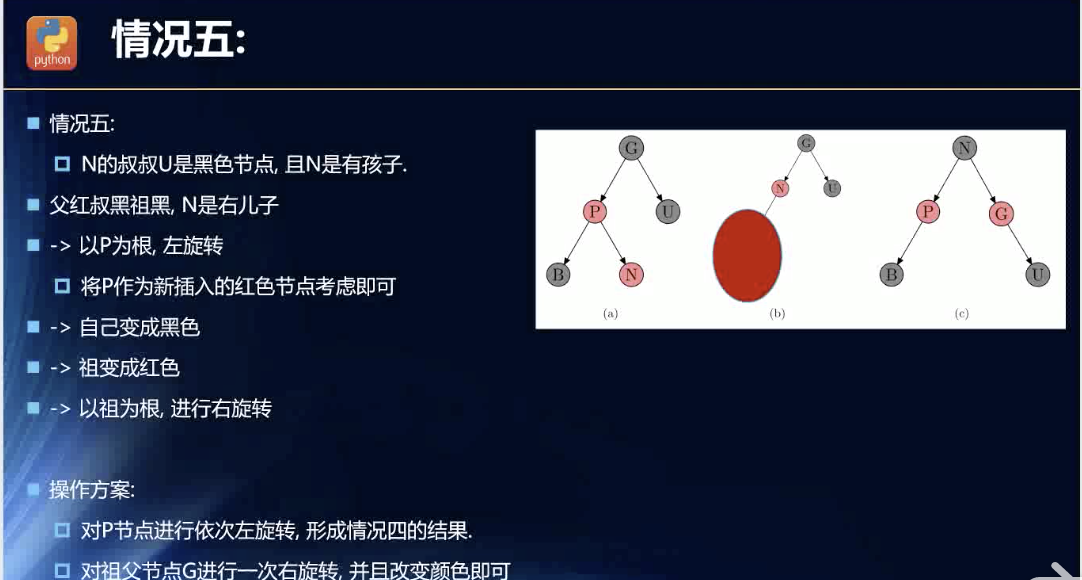
这次是通过转换为第四种情况，然后得出结果的。
我在这里突然想到了滑轮了，一头的重量多了，另一头就用力，拉一把，通过滑轮一转移，就微调了左右位置的重量了。

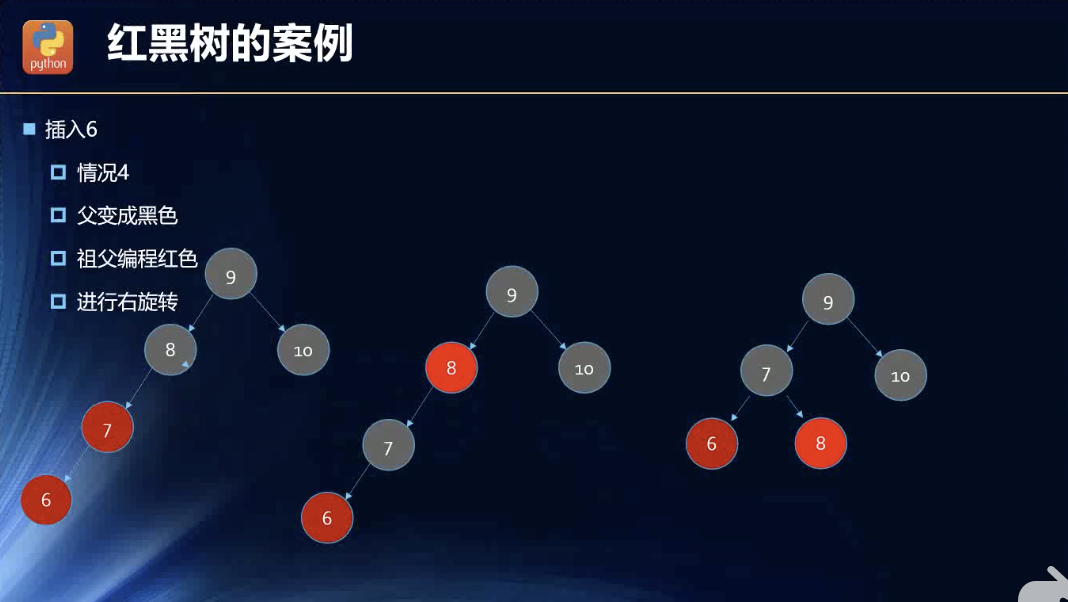
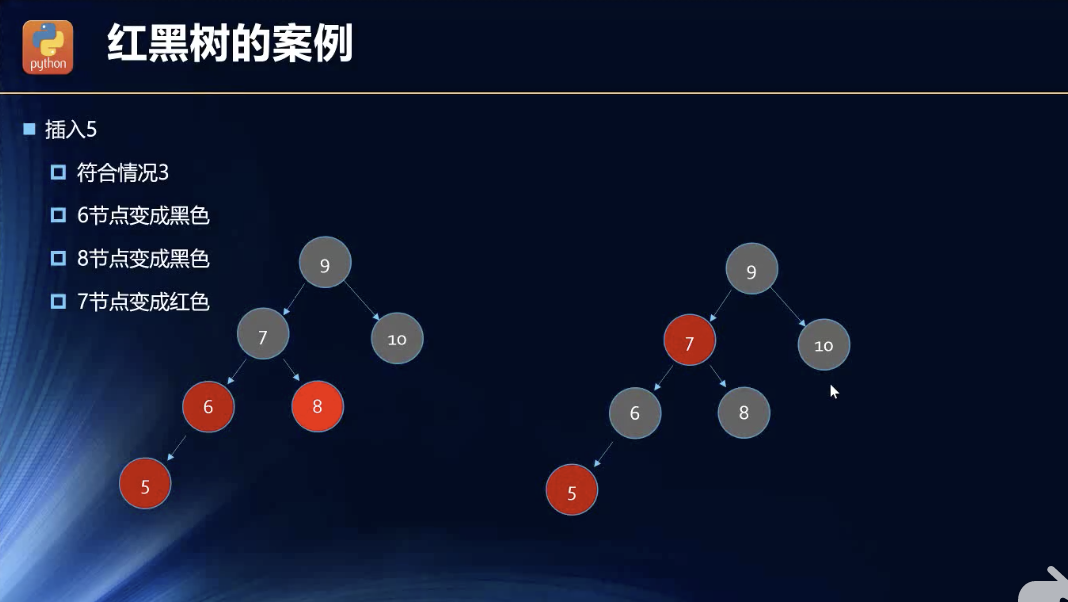
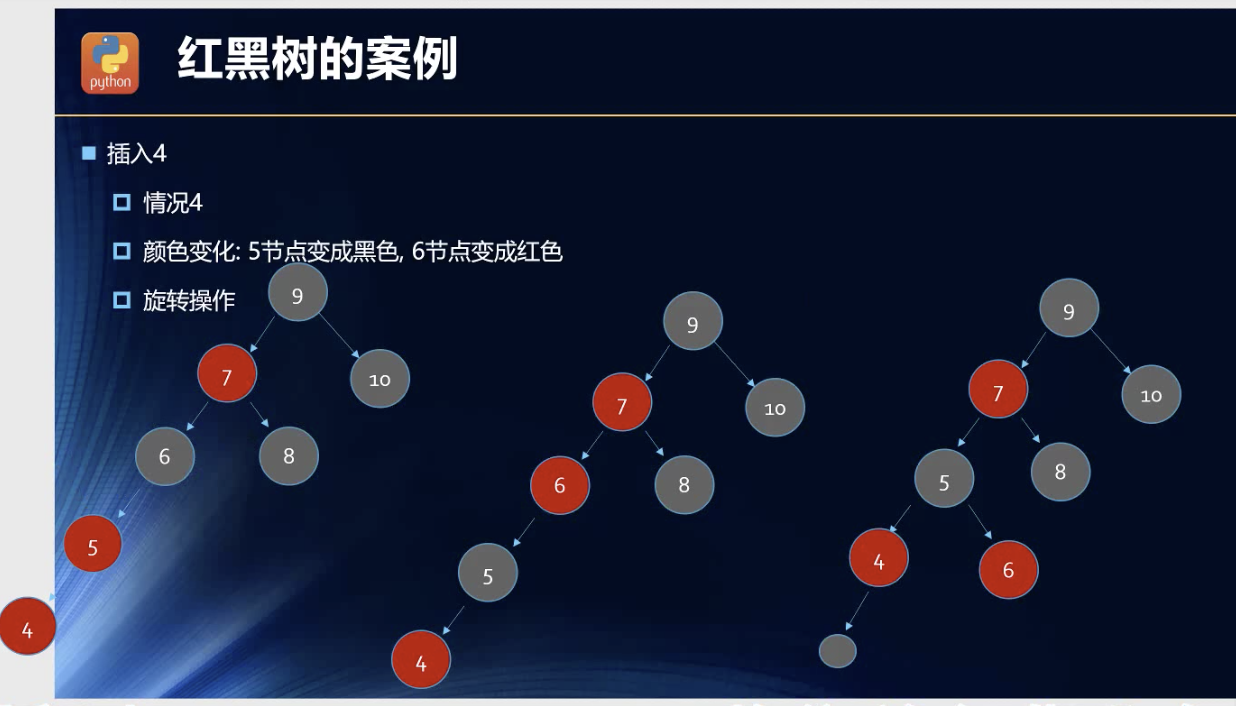
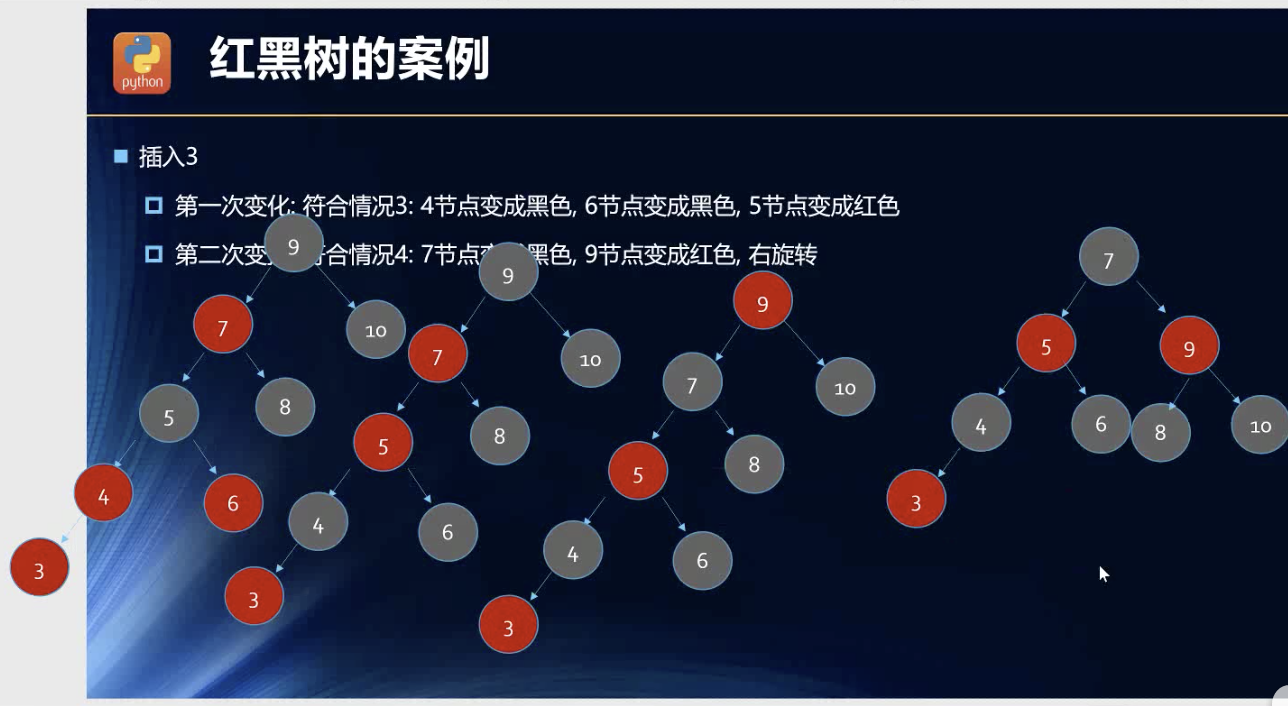
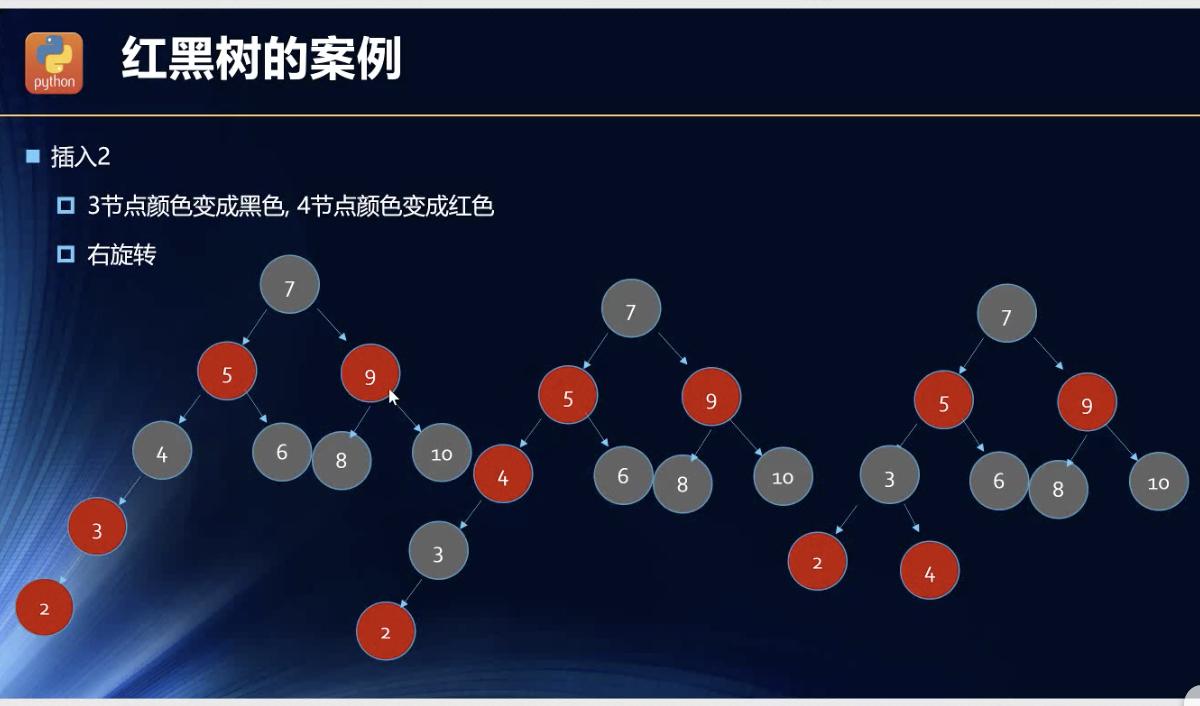
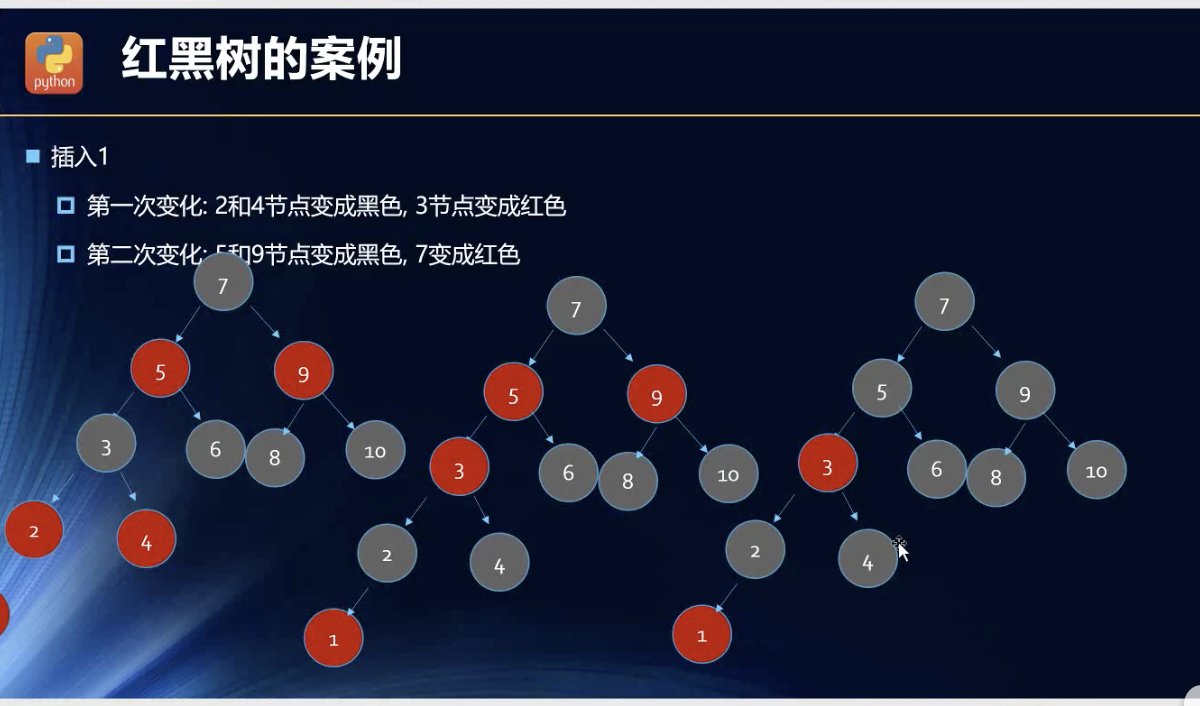
案例

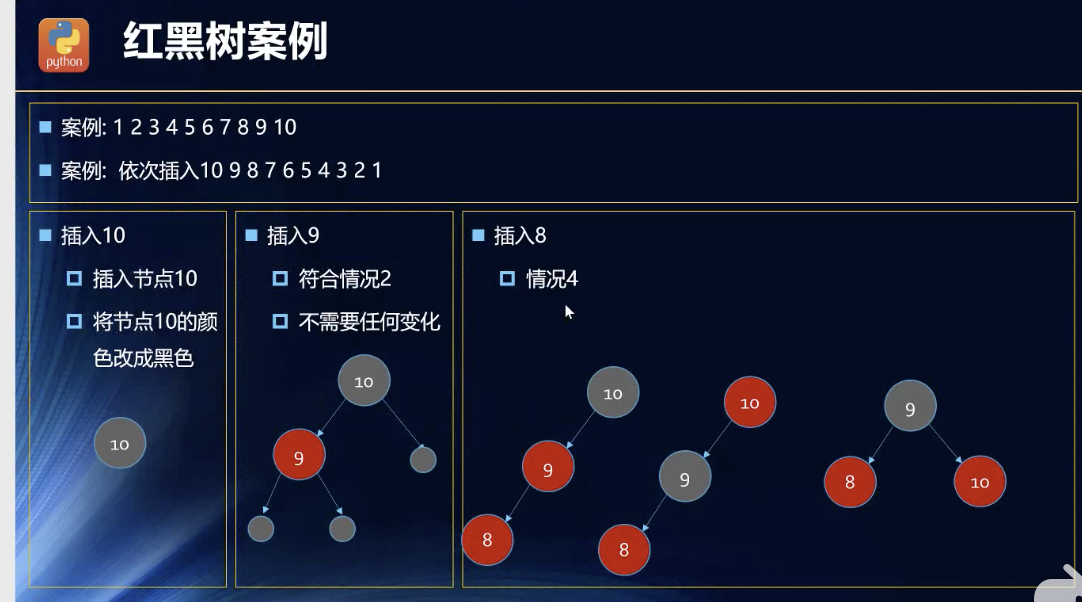
对于这三个没什么可以解释的。拿来主义了。

这里其实还是有些出乎我的意料的，我原本以为是要用旋转了，当然旋转是右旋转，符合情况四的。但是还可以如此操作，，，我觉得有些不合理，尤其是后面再插入了左节点的时候，变色还是要变的。看下面的实例了。