如何切割凹多边形

问题描述

如何把一个凹多边形切割成多个凸多边形？

切割凹多边形，常用的方法有向量方法（Vector Method） 和旋转法（Rotational Method）。

基本思路都是每次利用切割方法切割一次凹多边形，然后判断切割后的图形是否为凹多边形，若仍有凹多边形，则继续切割。

所以这里需要一个前置知识：如何判断任意多边形是否为凹多边形，具体可以看我之前的文章 《如何判别凹多边形》。

本文主要介绍利用 向量方法 来切割凹多边形。

向量方法

1. 找出异号的边向量叉积

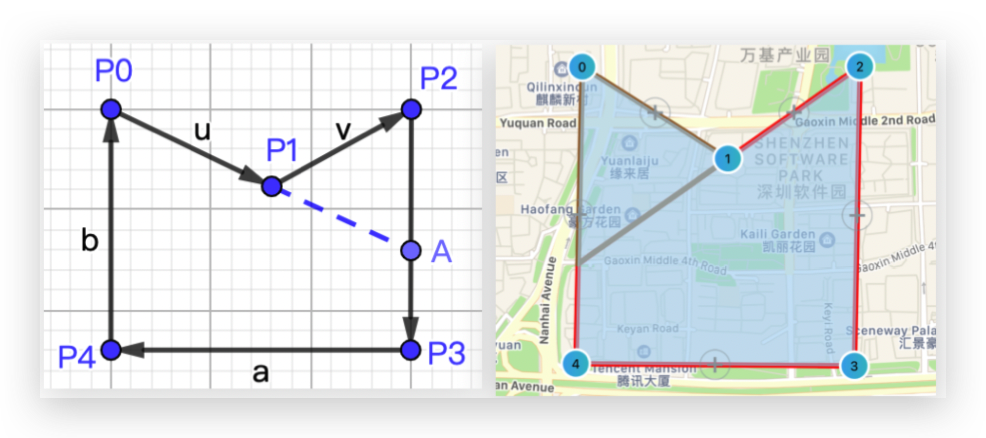
回顾《如何判别凹多边形》一文，我们知道凹多边形的边向量叉积存在异号的情况，如下图：

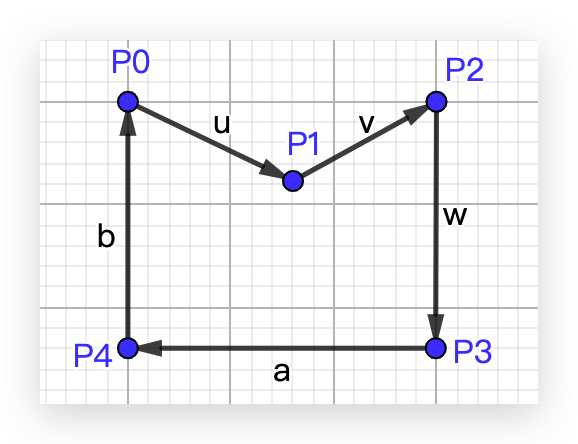
多边形 [P0, P1, P2, P3, P4] 的边向量叉积情况如下：

可以看到 的结果是大于 0 的，其余都是小于零。p0p1 和 p1p2 的边向量叉积结果是这里唯一异号的。

我们这里约定组成该凹多边形的点是按照顺时针排列的，所以如果边向量叉积中出现大于 0 的情况，则可以判断这两条边是凹进去的位置。即 p0p1 边是开始凹进去的位置，记录这条边的位置，接着对这条边进行下一步的处理。

注意：如果组成凹多边形的点是按照逆时针排列的，在按顺序计算的边向量的结果中，应该是以小于 0 的叉积结果作为判断。

2. 延长异号边进行切割

上一步骤中，我们找到了 p0p1 这条 “异号边”。我们将它延长，延长至跟多边形的一条边相交为止，如下图：

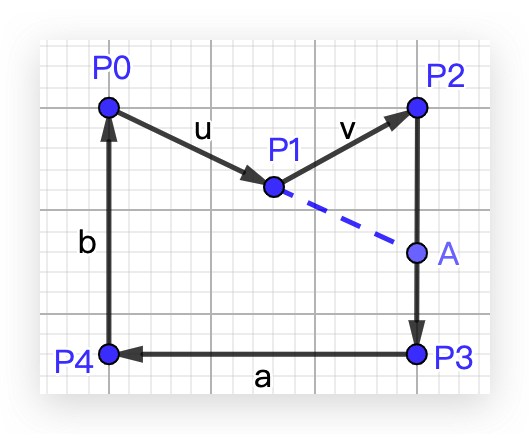
从图中可以看到，p0p1 延长线相交于 p2p3 上的一点 A。

这条延长线就是凹多边形的切割线，它把该凹多边形切割成 [p1, p2, A] 和 [p0, A, p3, p4] 两个多边形。

接着我们判断切割后的两个多边形是否仍存在凹多边形，发现并没有，则该凹多边形切割完成。

这里的描述看似简单，但是如果要把该问题抽象到代码中去处理，需要明确解决两个问题：

1. 如何找到交点位置，即交点所在的边和交点的坐标。
2. 得到交点坐标后，如何分割原数组，且得出点顺序是正确的两个多边形数组。

3. 找到交点位置

为了找到 p0p1的延长线相交于多边形上的哪一条边上，我们先回顾一下 《如何判断一个多边形是否合法》 一文中关于如何判断线段是否相交的方法：

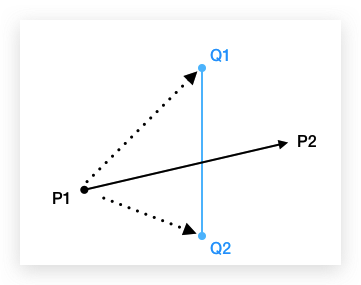
如果要判断 P1P2 和 Q1Q2 这两条线段是否相交，其中有一个步骤是这样的：

因为 在 的逆时针方向，那么： 因为 在 的顺时针方向，那么： 用 A 表示 $\vec{P_1P_2} \times \vec{P_1Q_1} $ 的叉积结果，用 B 表示 的叉积结果，那么 一条的线段的两个端点在另外一条线段两侧 这个几何现象可以用这个公式表示 ：

我们回顾到这一步就够了，这里的 P1P2 其实就相当于我们上面所用来切割多边形的延长线，Q1Q2 就相当于多边形上的任意一边。

为了找到延长线与多边形的一条边上的交点，我们可以利用这个方法，让延长线与多边形的边按顺序逐个进行计算，找到第一个结果为 的边，即可得知交点在哪里。

根据这里的判断方法，我们回到刚刚的凹多边形：

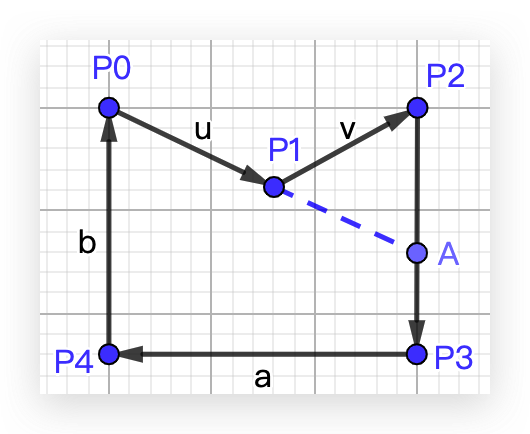
如上图， ，，

得出 cp1 乘以 cp2 的结果是小于 0 的，则交点会在 p2p3 边上。

然后我们就可以利用 p0、p1、p2、p3 这四个点，计算出直线函数，求出交点坐标 A 了，具体如何通过两个直线函数求交点坐标，这里就不赘述了。

这里上点代码来按照这个步骤进行理解：

/// 切割凹多边形为多个凸多边形，向量切割法
func divideConcavePolygon(vertexs: [CGPoint]) -> [[CGPoint]] {
    guard vertexs.count > 3 else { return [] }
    // 跳出外层循环的标志
    var breakFlag = false
    // 注意 vertexs 的点是顺时针排列的
    for index in 0..<vertexs.count {
        let index1 = (index + 1) % vertexs.count
        let index2 = (index + 2) % vertexs.count
        let p0 = vertexs[index]
        let p1 = vertexs[index1]
        let p2 = vertexs[index2]
        let crossProduct = crossproduct(vector1: (p0, p1), vector2: (p1, p2))
        // 如果叉积大于 0，说明 向量 p1p2 在 向量 p0p1 的逆时针方向
        // 即 p0p1 为异号边
        if crossProduct > 0 {
            // 与多边形的其它边进行计算，找出交点位置
            for i in 0..<vertexs.count {
                let current = vertexs[i]
                let next = vertexs[(i + 1) % vertexs.count]
                // 跳过当前边（延长线的边）
                if index == i || index == (i + 1) % vertexs.count {
                    continue
                }
                let cp1 = crossproduct(vector1: (p0, p1), vector2: (p0, current))
                let cp2 = crossproduct(vector1: (p0, p1), vector2: (p0, next))
                // 找到交点所在的边 即 current 和 next 组成的边
                if cp1 * cp2 < 0 {
                    // TODO: - 根据延长线和交点所在的边，计算出交点坐标 newPoint
                    // TODO: - 切割多边形数组，把 newPoint 添加到数组里
                    // 跳出内嵌套的循环，并标记需要跳出外循环
                    breakFlag = true
                    break
                }
            }
        }
        if breakFlag { break }
    }
    // TODO: - 返回切割后的凸多边形数组
    return polygons
}

4. 分割原数组

通过异号边延长线进行切割，得到交点坐标 A 后，我们还需要分割原数组，得到两个多边形的数组。

我们再次回到上面的凹多边形：

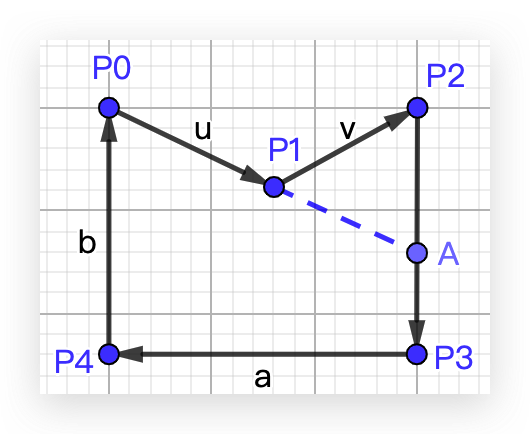
我们希望分割原坐标数组为 [p1, p2, A] 和 [p0, A, p3, p4] ，观察数组的点都是按照顺时针排列的，这个顺序很重要，一来可以确保多边形的形状，二来可以继续用我们上面的切割方法继续对剩下的多边形切割。

原多边形数组是 [P0, P1, P2, P3, P4] ，将其转换成数组索引查看为 [0, 1, 2, 3, 4]，观察可知，我们需要截取出 [1, 2] ，然后剩下 [0, 3, 4 ] ，再在合适的位置插入 A 的坐标即可。

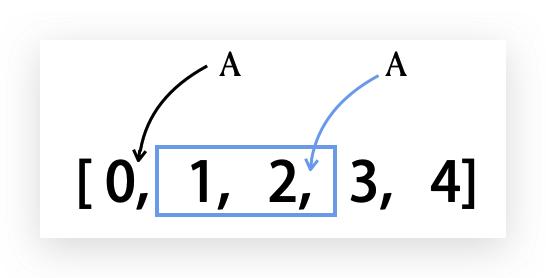
我们添加个 splice 的扩展方法，可以截取数组里的一个区间，这个方法是 mutating 的，也会改变原数组：

extension RangeReplaceableCollection {
    mutating func splice<R: RangeExpression>(range: R) -> SubSequence where R.Bound == Index {
        let result = self[range]
        self.removeSubrange(range)
        return result
    }
}

结合上面的凹多边形图片观察，交点 A 是在 p2p3 上的，即在数组索引 current = 2 和 next = 3 之间，至于异号边的索引为 index0 = 0 和 index1 = 1

var polygon2 = vertexs
var polygon1 = Array(polygon2.splice(range: index1...current))
// 插入交点 A 坐标
polygon1.append(A)
polygon2.insert(A, at: index0 + 1)

这里还要注意一种情况，就是交点坐标所在边的索引小于异号边索引的情况，可以用这样一副图说明：

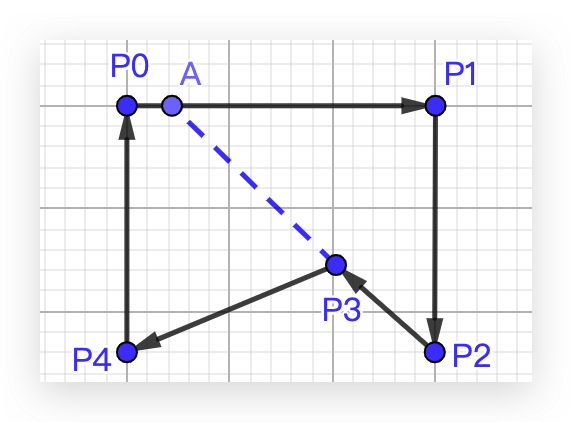
如图所示的凹多边形，交点 A 在 p0p1 上，即在数组索引 current = 0 和 next = 1 之间，至于异号边的索引为 index0 = 2 和 index1 = 3

这里贴出一段代码，便于理解这里区间的截取：

if current > index0 {
    var polygon2 = vertexs
    // current 大于 index0，则分割区间为 [index1, current]
    var polygon1 = Array(polygon2.splice(range: index1...current))
    // 插入交点 A 坐标
    polygon1.append(A)
    polygon2.insert(A, at: index0 + 1)
} else {
    var polygon2 = vertexs
    // current 小于 index0，则分割区间为 [current+1, index0]
    var polygon1 = Array(polygon2.splice(range: current + 1...index0))
    // 插入交点 A 坐标
    polygon1.append(A)
    polygon2.insert(A, at: index0 + 1)
}

5. 注意坐标系

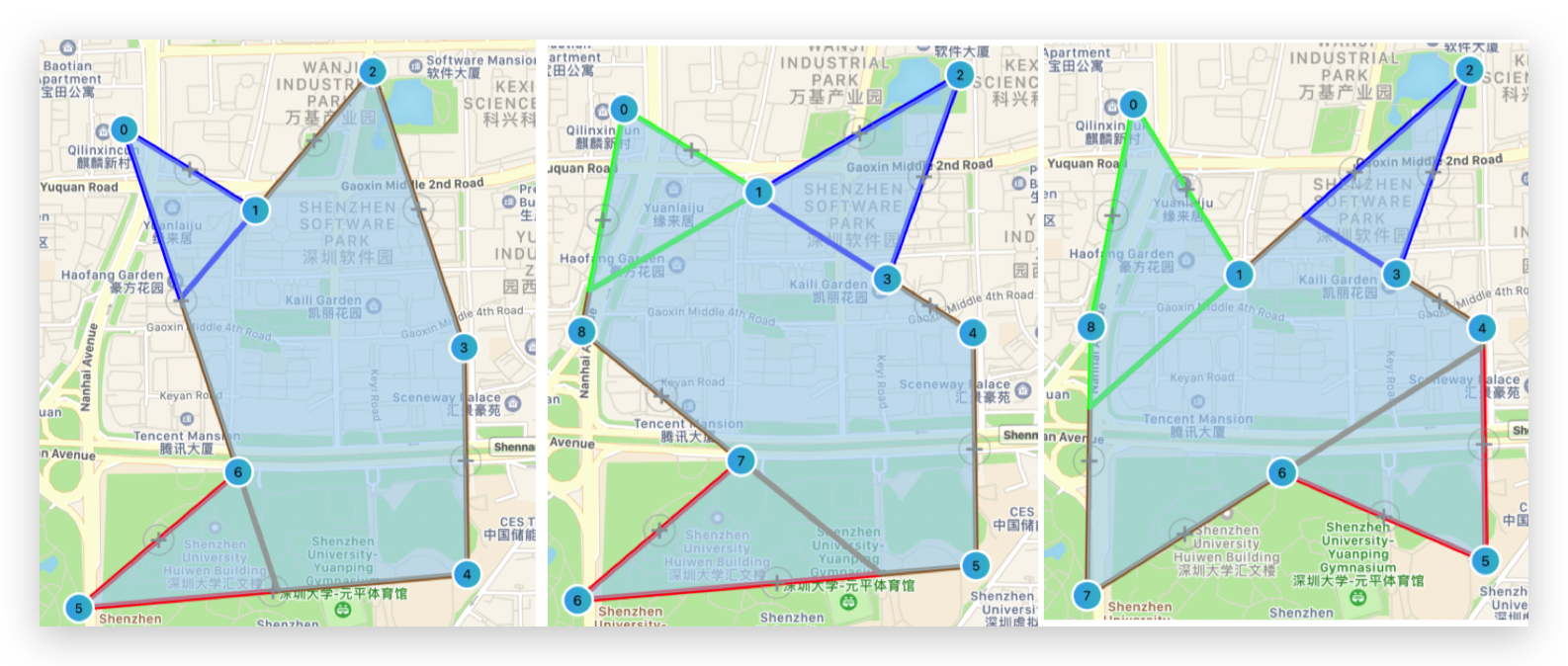
至此，分割凹多边形的向量方法已经讲解完毕了。我在 iOS 上做个 Demo 验证这个算法的时候，一开始发现切割的位置不太对，如下图：

从图中可以看出，实际切割的位置跟我推演算法时想象的位置是相反的，我百思不得其解。

后面才想起 iOS 的 x y 坐标系跟几何上的是不一样的，Y 轴的正方向是向下的。因此在算法的眼里，这个绘制出来的图形其实是上下颠倒的，因此算法并没有问题。这里特意提醒注意一下。