反向传播

反向传播

Back Propagation（梯度反向传播）实例讲解 - 马索萌的文章 - 知乎 https://zhuanlan.zhihu.com/p/40378224

BP的目的

首先我们要搞清楚两个问题

1. 为什么要求梯度？
2. 求关于谁的梯度？

上图展示了一个神经网络。神经网络可以看作是一个函数 ， 是输入， 是输出， 是 的参数。 的真实值是我们的目标，但我们有的只是一些 和与之对应的真实的 的值，所以我们要用到这两个值去估计 的真实值。这个问题可以看成下面的优化问题（优化问题即求函数最小值）

其中我们令 ，并称之为误差项。我们的目标就是求一组 使得 最小。求解这类问题有个经典的方法叫做梯度下降法（SGD, Stochastic Gradient Descent），这个算法一开始先随机生成一个 ，然后用下面的公式不断更新 的值，最终能够逼近真实结果。

其中 是当前的误差 关于 的梯度，它的物理意义是当 变化的时候 随之变化的幅度， 叫做学习率，通常在 以下，用来控制更新的步长（防止步子太大扯到蛋哈哈）。所以，开头的两个问题答案就有了：求梯度的原因是我们需要它来估算真实的 ，求的是误差项 关于参数 的梯度。

链式法则—BP的基础

在正式推导BP之前，我们首先需要回忆一下求导数的链式法则，这个是BP的基础和核心。假设 ，那么 。我们知道 ，那么如何求 对 的导数 呢？这个时候链式法则就出场了，根据微积分的知识 ，即复合函数的求导可以使用乘法法则，也称为链式法则，待会儿我们会用到。上面给出的是单变量的情况，多变量同样适用。

Back Propagation By Example

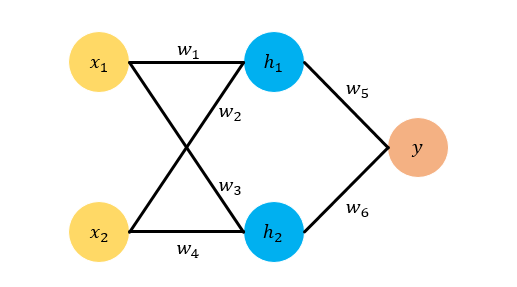
现在我们用一个例子来讲解BP，如下图所示，我们选取的例子是最简单的feed forward neural network，它有两层，输入层有两个神经元 ，隐藏层有两个神经元 ，最终输出只有一个神经元 ，各个神经元之间全连接。为了直观起见，我们给各个参数赋上具体的数值。我们令 ，然后我们令 的真实值分别是 ，令 的真实值是 。这样我们可以算出 的真实目标值是 。

网络结构示意图，一个简单的两层Feed Forward Netowrk

那么为了模拟一个Back Propagation的过程，我们假设我们只知道 ，以及对应的目标 。我们不知道 的真实值，现在我们需要随机为他们初始化值，假设我们的随机化结果是 。下面我们就开始来一步步进行Back Propagation吧。

首先，在计算反向传播之前我们需要计算Feed Forward Pass，也即是预测的 和误差项 ，其中 。根据网络结构示意图，各个变量的计算公式为：

现在Feed Forward Pass算完了，我们来计算Backward Pass。 是神经网络预测的值，真实的输出是 。那么，要更新 的值我们就要算 ，根据链式法则有

因为 ，所以

而 ，所以

把上面两项相乘我们得到

运用之前梯度下降法的公式更新 ，得到新的 。其中我们假设 （并且后面所有的 都等于 ）

同理，我们可以按照相同的步骤计算 的更新公式

下面我们再来看 ，由于这四个参数在同一层，所以求梯度的方法是相同的，因此我们这里仅展示对 的推导。根据链式法则

其中 在求 的时候已经求过了。而根据 我们可以得到

又根据 我们可以得到

因此我们有下面的公式

现在我们代入数字并使用梯度下降法更新

然后重复这个步骤更新

Great！现在我们已经更新了所有的梯度，完成了一次梯度下降法。我们用得到的新的 再来预测一次网络输出值，根据Feed Forward Pass得到 ，那么新的误差是 ，相比于之前的 确实是下降了呢，说明我们的模型预测稍微准了一点。只要重复这个步骤，不断更新网络参数我们就能学习到更准确的模型啦。

如果你看到了这里，那么恭喜你，你已经学会Back Propagation了。这么看下来，Back Propagation是不是很简单呢？