拉普拉斯算子

拉普拉斯算子

为什么 空间二阶导（拉普拉斯算子）这么重要？ - 郑易之的回答 - 知乎 https://www.zhihu.com/question/26822364/answer/288531247

拉普拉斯矩阵与拉普拉斯算子的关系 - superbrother的文章 - 知乎 https://zhuanlan.zhihu.com/p/85287578

在图网络深度学习中（graph deep learning）中，拉普拉斯矩阵是很常用的概念，深入理解其物理含义非常有助于加深对GNN模型的理解。

先说结论：

图拉普拉斯矩阵，如果把它看作线性变换的话，它起的作用与数学分析中的拉普拉斯算子是一样的。也就是说拉普拉斯矩阵就是图上的拉普拉斯算子，或者说是离散的拉普拉斯算子。

如果 是欧式空间中的二阶可微实函数，那么

就是在欧式空间中求其二阶微分（散度）。（ 是拉斯矩阵算子）

如果 是图上定义的一组高维向量，那么

就是在图空间中求其二阶微分（散度）。（ 是图的拉普拉斯矩阵）

解释如下：

直接套用导数的定义，无法直观理解拉普拉斯矩阵的物理含义。从散度入手，才是正确的打开方式。

梯度（矢量） ：梯度 “ ” 的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该方向处沿着该方向（此梯度方向）变化最快，变化率最大（为该梯度的模）。假设一个三元函数 在空间区域 内具有一阶连续偏导数，点 ， 称向量

为函数 在点 处的梯度，记为 或

其中：

称为（三维）向量的微分算子或 Nabla 算子。

散度（标量） 散度 “ “ （divergence）可用于表针空间中各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性。当 ，表示该点有散发通量的正源（发散源）；当 表示该点有吸收能量的负源（洞或汇）；当 ，表示该点无源。

拉普拉斯算子： 拉普拉斯算子（Laplace Operator）是 维欧几里得空间中的一个二阶微分算子，定义为梯度（ ）的散度（ ）。

笛卡尔坐标系下的表示法：

维形式

下面推导离散函数的导数：

则我们可以将拉普拉斯算子也转化为离散形式（以二维为例）

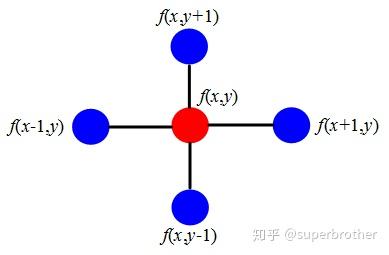
现在用散度的概念解读一下：

• 如果 ，可以近似认为中心点 的势和其周围点的势是相等的， 局部范围内不存在势差。所以该点无源
• ，可以近似认为中心点 的势低于周围点，可以想象成中心点如恒星一样发出能量，补给周围的点，所以该点是正源
• ,可以近似认为中心点 的势高于周围点，可以想象成中心点如吸引子一样在吸收能量，所以该点是负源

另一个角度，拉普拉斯算子计算了周围点与中心点的梯度差。当 受到扰动之后，其可能变为相邻的 之一，拉普拉斯算子得到的是对该点进行微小扰动后可能获得的总增益 （或者说是总变化）。

我们现在将这个结论推广到图： 假设具有 个节点的图 ，此时以上定义的函数 不再是二维，而是 维向量： ，其中 为函数 在图中节点 处的函数值。类比于 在节点 处的值。对 节点进行扰动，它可能变为任意一个与它相邻的节点 , 表示节点 的一阶邻域节点。

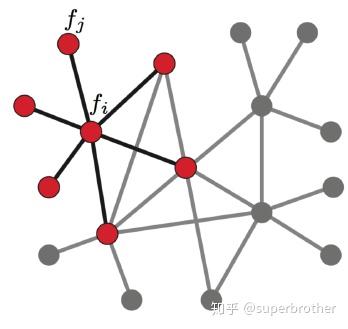
我们上面已经知道拉普拉斯算子可以计算一个点到它所有自由度上微小扰动的增益，则通过图来表示就是任意一个节点 变化到节点 所带来的增益，考虑图中边的权值相等（简单说就是1）则有：

而如果边 具有权重 时，则有：

由于当 时表示节点 不相邻，所以上式可以简化为： 继续推导有：

其中 是顶点 的度；

是 维的行向量， 是 维的列向量；

表示两个向量的内积。

对于所有的 个节点有：

这里的就是拉普拉斯矩阵 根据前面所述，拉普拉斯矩阵中的第 行实际上反应了第 个节点在对其他所有节点产生扰动时所产生的增益累积。直观上来讲，图拉普拉斯反映了当我们在节点 上施加一个势，这个势以哪个方向能够多顺畅的流向其他节点。谱聚类中的拉普拉斯矩阵可以理解为是对图的一种矩阵表示形式。