欧拉公式

欧拉公式

“上帝公式”(欧拉公式)真的神到无法触碰？ - 李狗嗨的文章 - 知乎 https://zhuanlan.zhihu.com/p/48392958

https://www.bilibili.com/video/BV1Es411P7tr?from=search&seid=16927280055308104849

https://zhuanlan.zhihu.com/p/48391055

自然底数e怎么就“自然”了？

在《飞蛾真的是因为趋光所以扑火？》中，通过对飞蛾运动轨迹的简化表达得到了与自然常数 相关的等角螺旋线。自然常数 确实是一个奇妙的数字，这里的 并不仅仅代表一个字母，它还是一个数学中的无理常数，约等于 。

但你是否有想过，它到底怎么来的呢？为啥一个无理数却被人们称之为“自然常数”？

说到 ，我们会很自然地想起另一个无理常数 。 的含义可以通过下图中的内接与外切多边形的边长逼近来很形象地理解[1]。

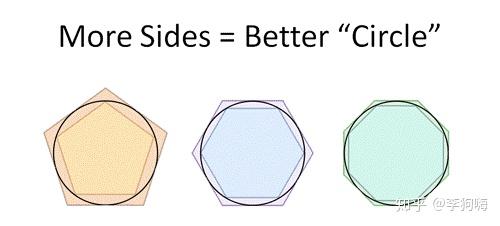(图片来源: betterexplained)

假设一个圆的直径为 ，其外切与内接多边形的周长可以构成 的估计值的取值范围上下限，内接与外切多边形的边越多，取值范围就越窄，只要边数足够多，取值范围上下限就可以越来越逼近圆周率 。 的简介及手动推导过程详见：《古人是如何寻找到π的？》

如果说 的计算很直观，那 呢？所以在此也用一种图解法来直观理解 。

首先，我们需要知道 这个表示自然底数的符号是由瑞士数学和物理学家Leonhard Euler(莱昂纳德·欧拉)[2]命名的，取的正是Euler的首字母“ ”。

Leonhard Euler (1707-1783) (图片来源: Wikipedia)

但实际上，第一个发现这个常数的，并非欧拉本人，而是雅可比·伯努利（Jacob Bernoulli）。

伯努利家族

伯努利家族是17〜18世纪瑞士的一个赫赫有名的家族，其中出了很多著名的数理科学家，雅可比·伯努利是约翰·伯努利（Johann Bernoulli）的哥哥，而约翰·伯努利则是欧拉的数学老师。总之，大佬们之间有着千丝万缕的联系。

要了解 的由来，一个最直观的方法是引入一个经济学名称“复利(Compound Interest)”。

复利率法（英文：compound interest），是一种计算利息的方法。按照这种方法，利息除了会根据本金计算外，新得到的利息同样可以生息，因此俗称“利滚利”、“驴打滚”或“利叠利”。只要计算利息的周期越密，财富增长越快，而随着年期越长，复利效应亦会越为明显[3]。—— 维基百科

但为了便于理解，在引入“复利模型”之前，先试着看看更基本的 “指数增长模型”。

我们知道，很多细菌是通过二分裂进行繁殖的，假设某种细菌 天会分裂 次，也就是 个增长周期为 天，如下图，这意味着：每一天，细菌的总数量都是前一天的两倍[4]。

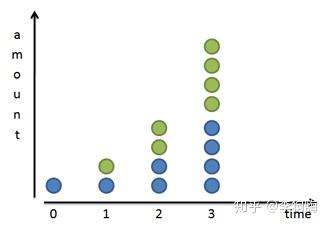(图片来源: betterexplained)

显然，如果经过 天（或者说，经过 个增长周期）的分裂，就相当于翻了 倍。即，在第 天时，细菌总数将是初始数量的 倍。

如果细菌的初始数量为 ，那么 天后的细菌数量即为 ：

如果假设初始数量为 ，那么 天后的细菌数量则为 ：

因此，只要保证所有细菌 天分裂 次，不管初始数量是多少，最终数量都将是初始数量的 倍。因此，此计算关系也可以写为：

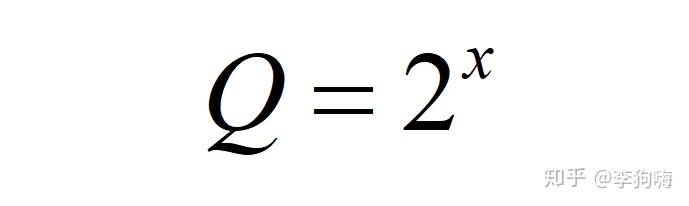
上式含义是：第 天时，细菌总数量是细菌初始数量的 倍。

如果将 “分裂”或“翻倍”换一种更文艺的说法，也可以说是：“增长率为 ”。也就是说，可以将上式写为：

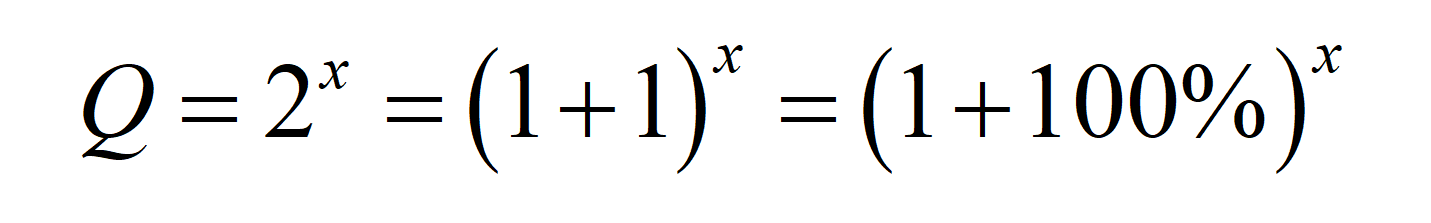
而当增长率不是 ，而是 、 之类的时候，则只需要将上式的 换成想要的增长率即可。这样就可以得到更加普适的公式：

这个公式的数学内涵是：一个增长周期内的增长率为 ，*在增长了 个周期之后，总数量将为初始数量的 倍。**

以上为指数增长的一个简单实例，下面来看看雅可比·伯努利的发现：

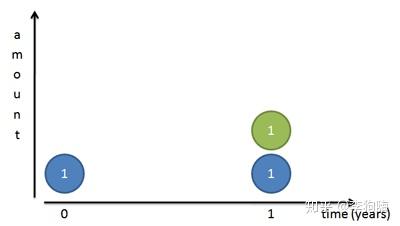
假设你有 元钱存在银行里，此时发生了严重的通货膨胀，银行的利率飙到了 （夸张一下，为了方便计算）。如果银行一年付一次利息，自然在一年后你可以拿到 元的本金（蓝色圆）和 元的利息（绿色圆），总共两元的余额。

(图片来源: betterexplained)

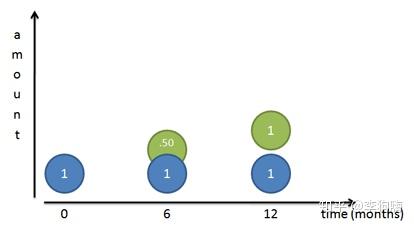
现在银行的年利率不变，但银行为了招揽客户，推出一项惠民政策，每半年就付一次利息。那么到第六个月（也就是半年）的时候，你就能够提前从银行拿到 元的利息了。

(图片来源: betterexplained)

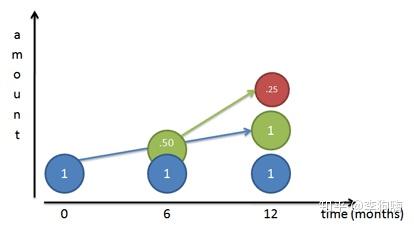
机智的你会马上把这 元的利息再次存入银行，这 元的利息也将在下一结算周期产生利息(红色圆)，专业术语叫“复利”，那么年底的存款余额将等于 元。

(图片来源: betterexplained)

此时，我们可以换个角度这样看：即，每个结算（增长）周期为半年，每半年的利率是 （或者说 ），一年结算两次利息，且第一次结算完后，立马将利息存入。此时我们的计算公式和结果如下：

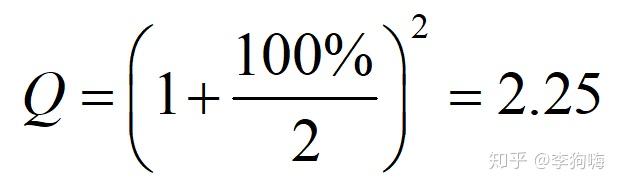
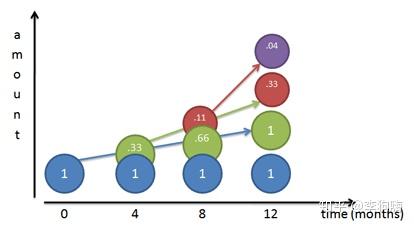
继续，假设现在银行为了和其他银行抢生意，短期不想赚钱了，每四个月就付一次利息！而机智的你依然一拿到利息就立马存入，与半年结算一次利息类似：即，每个结算周期为四个月，每四个月的利率是 （或者说 ），一年结算三次利息，且前两次结算完后，都立马将所有利息存入。

(图片来源: betterexplained)

此时计算公式和结果如下：

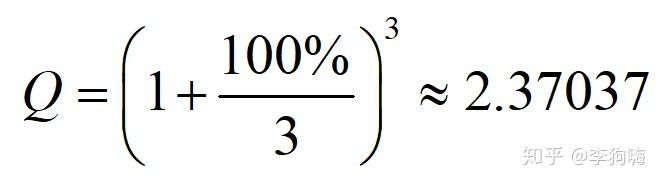
我的天，年利率虽然没有变，但随着每年利息交付次数的增加，你年底能从银行拿到的钱居然也在增加！

那么是不是会一直增大到无穷大呢？想得倒美…

现在假设存款人和银行都疯了，银行在保证年利率为 的前提下连续不断地付给存款人利息，存款人天天呆在银行不走，拿到利息就往银行里存。这样，所得利息即所谓“连续复利”。

但是，你会发现，似乎有一个“天花板”挡住了你企图靠 块钱疯狂赚取 个亿的小目标，这个“天花板”就是 ！

如果，我们进行一系列的迭代运算，我们将看到以下结果：

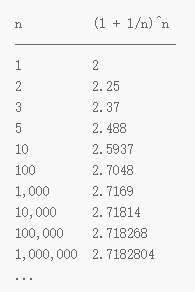
其中， 指的是一年中结算利息的次数。

只要在年利率保持 不变的情况下，不断地提高利息的结算次数，余额就将会逼近

然后，终于可以祭出这个高等数学微积分里计算 的一个重要极限了：

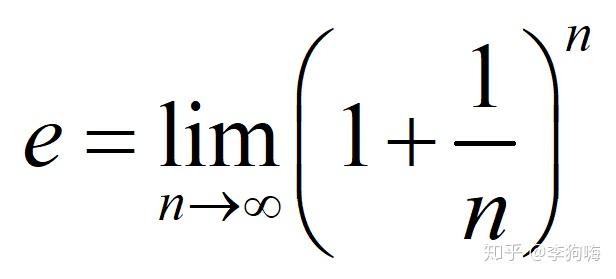
现在再回头看这个重要极限，想必会有更加直观的理解。

也就是说，就算银行的年利率是 ，再怎么求银行给你“复利”，年底也不可能得到超过本金 倍的余额。况且，我是没见过哪个银行的年利率是 。

虽然正常的银行不会推出连续复利这种优惠政策，但在自然界中，大多数事物都处在一种“无意识的连续增长”状态中。对于一个连续增长的事物，如果单位时间的增长率为 ，那么经过一个单位时间后，其将变成原来的 倍。而生物的生长与繁殖过程，恰恰也类似于“利滚利”的过程。

再比如，在《飞蛾真的是因为趋光，所以扑火？》中引入并推导所得的等角螺线[5]：

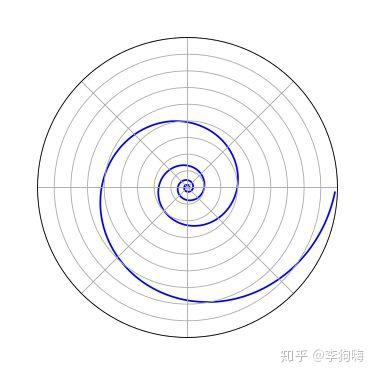等角螺线 (图片来源: Wikipedia)

如果用极坐标表示，其通用数学表达式为：

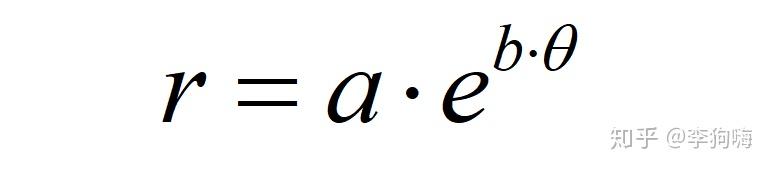
其中， 、 为系数， 螺线上的点到坐标原点的距离， 为转角。这正是一个以自然常数 为底的指数函数。

例如，鹦鹉螺外壳切面就呈现优美的等角螺线：

鹦鹉螺外壳 (图片来源: Wikipedia)

温带低气压的外观也像等角螺线：

温带低气压 (图片来源: Wikipedia)

就连旋涡星系的旋臂都像等角螺线：

旋涡星系 (图片来源: Wikipedia)

或许这也是 被称为“自然常数”的原因之一吧。当然，自然常数 的奇妙之处还远不止这些，一本书都写不完。

虚数

在说虚数(Imaginary Numbers)之前，应该先提大家更加熟悉的一个概念，那就是负数(Negative numbers)。负数的概念在小学数学里就有介绍，也就是说，小学生也应该能够自信地进行负数的各种运算，但是在公元 世纪以前，即使是当时欧洲著名的数学家，想让他理解“负数”这个概念也并不容易。

“负数”在当时被认为是荒谬的，就像公元500年之前，毕达哥拉斯学派的弟子希伯索斯(Hippasus)发现无理数（也称为无限不循环小数，如自然常数 ，见：《自然底数e怎么就“自然”了？》和圆周率 ，见：《古人是如何寻找到π的？》，它们都无法写成两个整数之比）一样。

Hippasus (图片来源：Wikipedia)

公元前 世纪，毕达哥拉斯学派认为“万物皆数”，世界上只有整数和分数(有理数)。而希帕索斯[1]却发现了令人震惊的“无限不循环小数”，即无理数，令该学派感到恐慌，并引发了第一次数学危机。有传言说最终希帕索斯被自己的老师毕达哥拉斯(Pythagoras)判决淹死。也有说法是被学派门人丢进海里淹死。

当人们在直观感受遭遇挑战的时候，人们往往先选择拒绝。

例如，当时的人们可以很直观地理解，如果你家有 条狗，后来送给别人家 条，你还剩下1条， 。但如果说你家有 条狗，然后送给别人家 条狗，那这是什么狗？！

所以，人们无法直观上理解的计算方法在当时是不能被接受的。以致于，1759年英国数学家Francis Maseres[2]，也会说：“Negative numbers darken the very whole doctrines of the equations.（负数使关于方程的所有学说变得毫无意义，即认为负数没有意义）”。

Francis Maseres (图片来源：Wikipedia)

即使是欧拉(Leonhard Euler)，也为“负数”的概念纠结了好一阵。不过现如今，认为负数“无用”或“不合逻辑”才是真的荒谬。

那为什么人们对负数的理解发生了 的大转变呢？因为我们发明了一种具有有用属性的理论上的数字，负数并不能很好地用来描述我们看得见、摸得着的可直观感受的事物，但却能很好地描述某种关系。

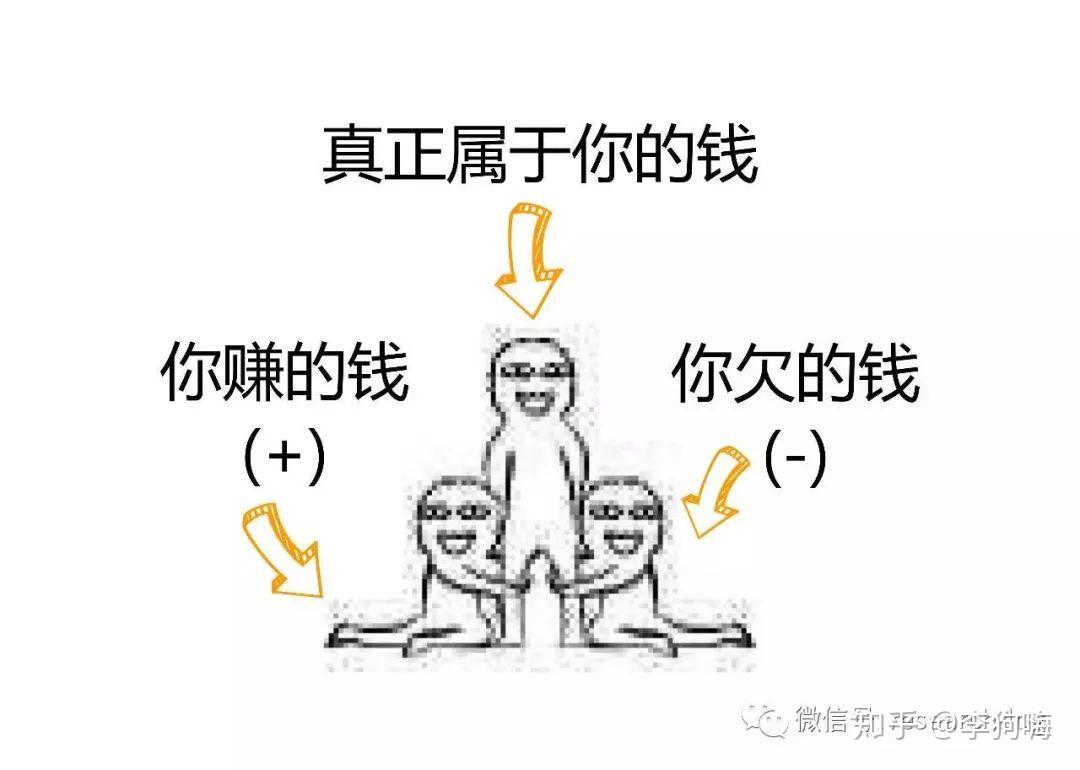
例如“债务”。人们会在日常支出中记录各种交易信息，如果欠别人 元，你会记录 ，在赚了 元以后，可以直接用 来计算属于自己的钱，而不需要更多的文字描述，负数已经将这种关系植入其中，既然有这种属性，又有什么理由说它是无用的呢？可见“关系”的重要性~

虚数也有相似的命运，从其名字就可以看出似乎受到过很不公正的待遇。一元二次方程 有两个解， 和 。那对于方程 呢？在解之前，我们不妨先假设 的解存在，就像负数一样，奇怪的概念往往其实有其自身的价值。

对于方程 ，其实可以写成 。我们将 “乘以 ” 看成是一种“变换”，通过两次这种变换，我们最终将 变为 。但我们不能通过和两个正数的相乘抑或是和两个负数的相乘来实现 到 的转变，以前也说过，“变换”并不改变问题本身，而只是改变了看待问题的角度，感兴趣的可见：《如何给文科生解释傅里叶变换？》。

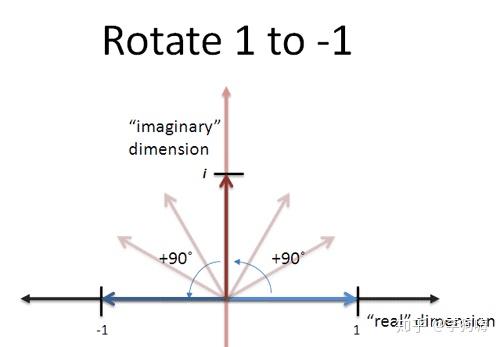
但是如果这种“变换”是“旋转”呢？听起来很新颖，但是我们把 定义为“逆时针旋转 角”的话，在包含两个正交轴的坐标系上，就能够实现 到 的转变。

而这个坐标系构成的平面也称为“复平面（横轴为实数轴(Real Dimension)，纵轴为虚数轴(Imaginary Dimension)）”，并用字母i 作为该情况下 的解，用来特指“逆时针旋转90°角”的变换[3]。

(图片来源: betterexplained)

那如果想顺时针旋转 呢？

答案是：乘以 就行了。

(图片来源: betterexplained)

而且如果乘以两次 ，和乘以两次 一样，得到的也是 。

如果分别乘以 次、 次、 次、 次、 次、 次 ，可以得到：

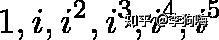
可以得到以下结论：

• （毫无疑问）
• （感觉是句废话）
• （上面已经说明了原因）
• （三次逆时针旋转 ，相当于顺时针旋转 ）
• （四次逆时针旋转 ，回到初始位置，循环结束）
• （开始下一循环，逆时针旋转 ）

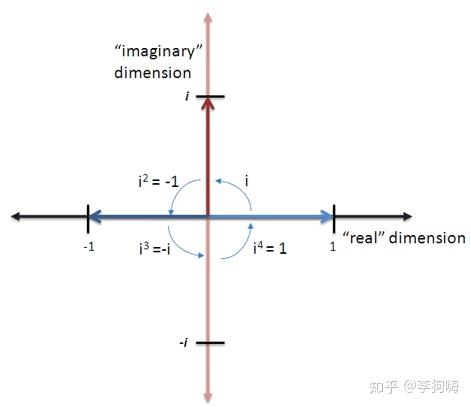(图片来源: betterexplained)

同时，上图也不知不觉地将数从一维的实数域拓展到了二维的复数域，即实数与虚数的组合。或者说：复数=实部+ 虚部。例如，一个复数 的实部为 ，虚部也为 ，则可以得到复数 。

复数Z 可以看作是复平面上的点 ，如下图。即沿着实轴方向前进 ，沿着虚轴方向再前进 ，其在实轴与虚轴上的投影值即为实部与虚部的值，其长度或“模(Modulus)”为该点到原点的距离为 ，该点与原点连线后与实轴正方向的夹角为 ，该角度称为幅角(Argument)。既然又有长度又有方向，因此复数也就可以看做是复平面上的一个矢量。

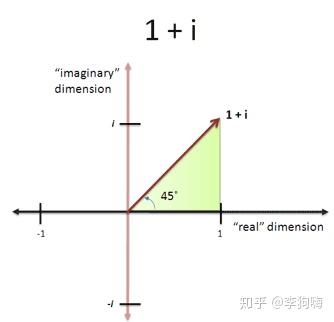(图片来源: betterexplained)

为了描述复平面上的任意一点，可以写成更为普遍的形式：

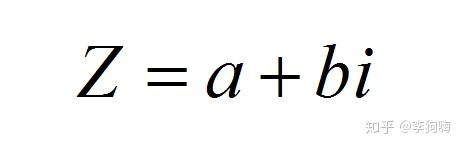
其中， 和 分别称为复数 的实部和虚部。

而 的长度或“模(Modulus)”为 点到复平面圆心处的距离：

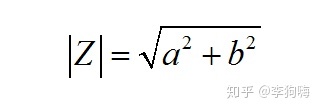
的幅角为

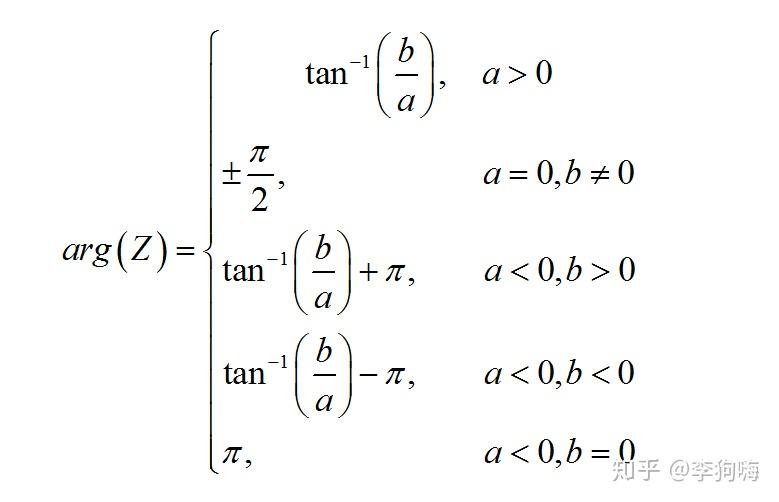
下面进行一个复数的计算实例，需要记住的一点是：两个复数相乘的结果就是：让它们的模长相乘得到最终的模长，让它们的幅角相加得到最终的幅角。

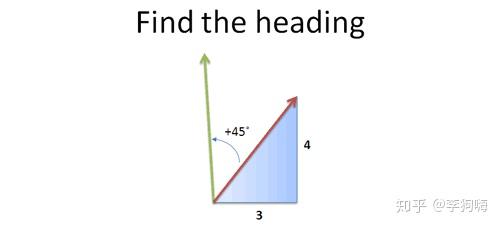
假设我们在一艘帆船上，现在帆船的航向是东北向，且每向东前进 个单位就会向北前进 个单位，如果现在想改变航向，使其沿逆时针方向旋转 ，那新的航向是怎么样的？

(图片来源: betterexplained)

如果放在复平面上，船的位置在圆心处，那么当前的航向可以直接用复数表示，即 。如果想逆时针转 可以让该复数与 相乘，因为 的幅角正好等于 。

计算过程为：

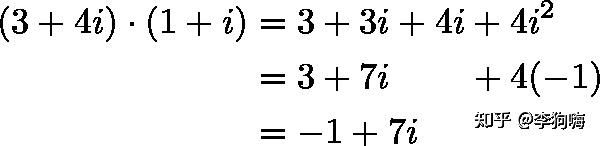
画出图就很直观了，新的航向是每向西前进 个单位就会向北前进 个单位。

(图片来源: betterexplained)

幅角为 。

注意，如果要保持航速不变的话还需要在上面计算结果的基础上再除以 ，因为复数 的模为 。

既然复数自带旋转属性、有大小、有方向，而正是虚数的存在才将一维的实数域提升或者说扩展到了二维的复数域，那么还有什么理由说虚数很虚呢？

欧拉公式

这个发表于公元1748年的数学公式，将三角函数与复指数函数巧妙地关联了起来。

其中， 为自然常数， 为虚数， 则是以弧度为单位的参数（变量）。

尤其是当参数 等于 的时候，欧拉公式可简化成为：

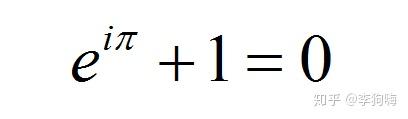
上式将5个微妙且看似无关的数学符号 紧密地联系了起来，其美妙之处让人称绝。 及弧度制的详细介绍及直观推导请分别参见：

莱昂纳德·欧拉简介

莱昂纳德·欧拉(Leonhard Euler) [1]1707年生于瑞士巴塞尔，他的父亲保罗(Paul Euler)是一位基督教牧师，他父亲原本也想将欧拉培养为一名牧师。

但巧的是他的父亲与伯努利家族关系很不错，而伯努利家族是17〜18世纪瑞士的一个赫赫有名的家族，其中出了很多著名的数理科学家。伯努利原籍比利时安特卫普，1583年遭天主教迫害迁往德国法兰克福，最后定居瑞士巴塞尔。其中以雅可比·伯努利（Jacob Bernoulli），约翰·伯努利（Johann Bernoulli），丹尼尔·伯努利（Daniel Bernoulli）这三人的成就最大。雅可比·伯努利是约翰·伯努利的哥哥，也就是首此发现自然常数e 的那位。而丹尼尔·伯努利是约翰·伯努利的儿子。

约翰·伯努利很早就看出了幼年欧拉的数学天赋，他劝说欧拉的父亲保罗，让欧拉从事数学研究领域的工作，并使他相信欧拉注定能成为一位伟大的数学家。

因此，13岁时就进入了巴塞尔大学学习的欧拉，虽然按照他父亲的意愿主修哲学和法律，并进入了神学系，但在每周星期六下午便跟随当时欧洲最优秀的数学家约翰·伯努利学习数学。

同一时期，约翰·伯努利的两个儿子——丹尼尔·伯努利和尼古拉·伯努利（Nicolas Bernoulli）——在位于俄国圣彼得堡的俄国皇家科学院[2]工作。在尼古拉因阑尾炎于1726年7月去世后，丹尼尔便接替了他在数学/物理学所的职位，同时推荐欧拉到数学/物理学所工作。

St. Petersburg Academy of Science (图片来源：Wikipedia)

考虑到当时俄国的持续的动乱，欧拉在1741年离开了圣彼得堡，到柏林科学院[3]就职。

Berlin-Brandenburgische Akademie der Wissenschaften (图片来源：Wikipedia)

在柏林，他出版了他最有名的两部作品：一部关于函数方面出版于1748年的《无穷小分析引论》和一部是关于微积分出版于1755年的《微积分概论》。在《无穷小分析引论》(Introduction to Analysis of the Infinity)中，欧拉提出了著名的“欧拉公式”。

欧拉公式的推导

开头介绍了欧拉公式的一种通用写法是：

其将复指数与正弦、余弦函数联系了起来。那么这是如何做到的？能否更加直观一点呢？

通常书本上给出的都是欧拉公式的验证而不是推导，例如，很多人会说：只要分别将两边的自然指数函数和三角函数用泰勒级数展开，即可得出两边相等的结论，但这只是验证而非真正的推导，就连《费曼物理学讲义》里面的计算也是如此。

为了让其更加易于理解，这里试着用直观的方式给予推导！

首先，需要记住的一点是：Euler方程等号两边都可以看作是描述在一个圆上的位置或者运动[4]。

如果我们用三角函数去描述圆心在复平面原点处的单位圆上的位置或圆周运动轨迹，当圆弧角为 弧度时，如图有：

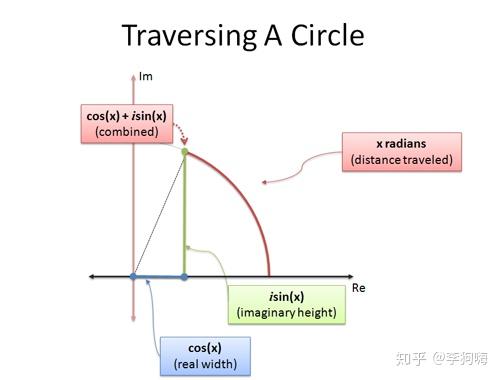(图片来源: betterexplained)

• 为当前圆周运动位置的横坐标
• 为当前圆周运动位置的纵坐标

因此采用复数 ，即可描述单位圆周上点的位置或运动轨迹。

用复数来描述坐标还比较好理解，那么欧拉公式左边的复指数又代表的是什么呢？（由于欧拉公式左边复指数中的实部为零，只包含虚部，因此也可以称之为虚指数）

先举个与实指数相关的例子，当看到 时，你可以把它看作是 个 连乘，但也可以换一个角度看。因为作为底数来说， 作为自然底数，是所有连续复利增长过程都共有的基本属性，其内涵的是单位数量在经过单位时间增长率为100%的连续复利增值后的最终结果，“连续复利”的定义请见：《自然底数e怎么就“自然”了？》。

我们可以将 改写为 ，其数学内涵可以解释为：单位数量在单位时间增长率为 的连续复利情况下，经过 个单位时间增长后的最终结果。

通式可以写为： 。

其中， 表示单位时间的增长率， 表示经历了多少个单位时间的增长，而 表示最终增长结果是初始值的多少倍。

因此，跳开数值本身的大小问题，我们把“乘以实指数”看成是初始值的一种“增长”或者说是对初始值的一种“推动”作用（这里的“初始值”是具有大小和方向属性的“复数”，复数包含实数和虚数，表达式可写为：复数=实部+ 虚部）。

再例如实数 ，可将其看做是：单位时间增长率为 ，初始值以该增长率连续复利增长，经过单位时间后最终结果将是 。

这里先只考虑了增长率为实数时的增长作用，而以实数为增长率的这种“增长”或“推动”是沿着初始值的方向进行的（复数可以看作是复平面上的矢量，因此具有方向属性）。

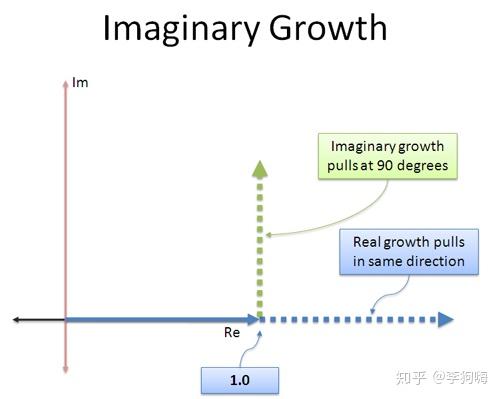(图片来源: betterexplained)

而虚指数所带来的增长作用就和实指数有所不同，虚指数的增长作用的方向与初始值的方向垂直，且随着数值的变化始终保持着这种垂直的关系，详情请见：《虚数i真的很“虚”吗？》。这种增长方式并不改变数的大小，而只改变复数的方向！例如，让任何数乘以虚数 ，都不会改变数的大小（或模长），而是改变数的方向。

在《自然底数e怎么就“自然”了？》中已经给出了自然底数 的定义式：

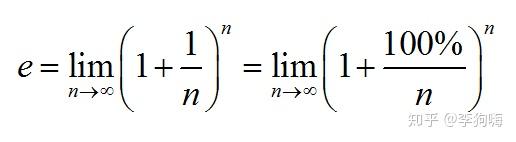
不过在上式中，我们假设的增长率为实数，但是，如果增长率为虚数呢？

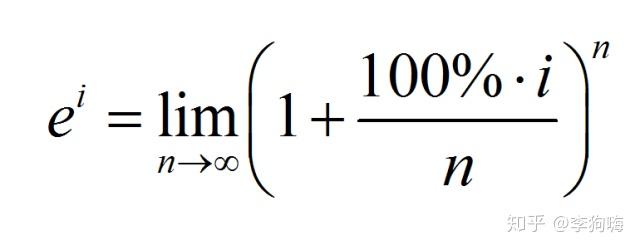
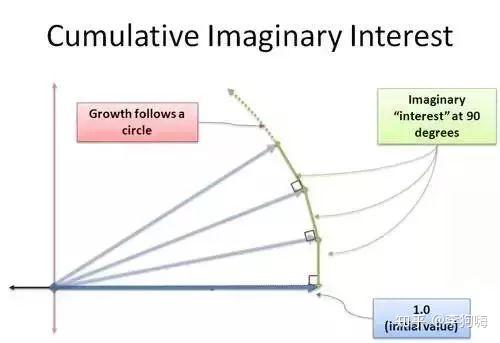
其增长的示意图如下图所示：

(图片来源: betterexplained)

现在，“新的增长率”其实一直是沿着复数的垂直方向。并且这并不会改变复数的长度，但有人会提出质疑，因为上图所示的示意图是由一个个直角三角形组成，斜边当然比直角边更大。

但要知道，我们正在处理的是一个极限问题，当 （其实n可以看作到达最后结果所经历的增长步数，这个增长步数是我们人为设定的，上图中的每个绿色的直角边都代表一步），则绿色的直角边将越接近斜边。

最终将得到的结果是：复数长度（模长）不变的连续旋转。这是处理其与正弦、余弦之间关系的核心概念，当复数的增量始终与复数的方向保持垂直，得到的轨迹必将是一个圆！

下面用公式来证明这一过程：

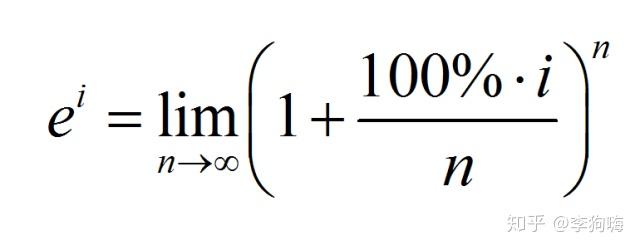
复数的模长为实部平方与虚部平方的和的平方根；转角为虚部除以实部的反正切值。

对于上式，如果 ，则结果为 ；（注意复数的运算法则是：所有模长增量相乘得到最终模长；所有转角增量相加得到最终转角）

如果上式中 ，则结果为 ；

即，将 的一步完成增长变为了 的两步完成增长。

那么当 时，分步增长就变成了连续增长问题；

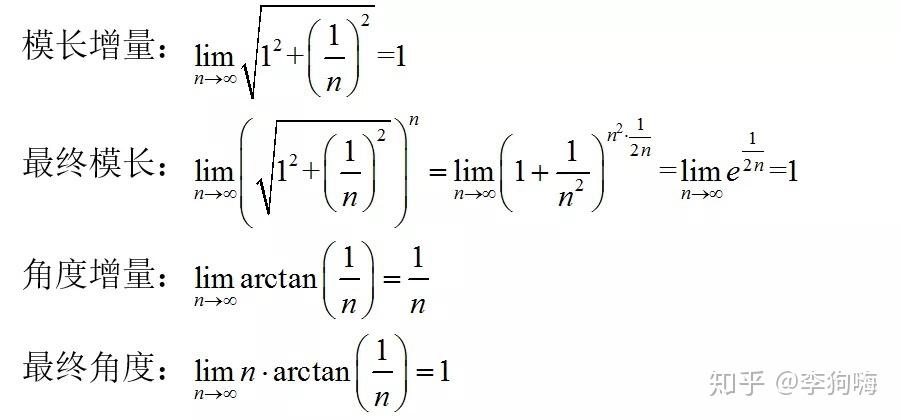
实际上就是复数 逆时针旋转，每一小步的增长方向都和复数指向方向垂直，且保证模长不变，因此极限状态就是圆周运动，最后转动角度为 弧度。

即 。

那对于更为普遍 呢？当 时；

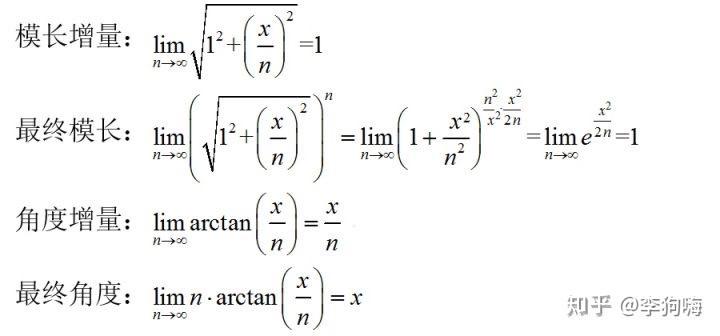
实际上也是复数 逆时针不断旋转，每一小步的转动方向都和复数指向方向垂直，且保证模长不变，因此极限状态也是圆周运动，所以当然可以用欧拉公式等号右边三角函数法定义的单位圆周上的点来完全等效（注意：这里的 都采用弧度制）。

即

如果 是随时间线性变化的参数，则可以得到以下三维等径螺旋线，该螺旋线在复平面上的投影是一个圆，投影点在圆上的运动为匀速圆周运动[5]。

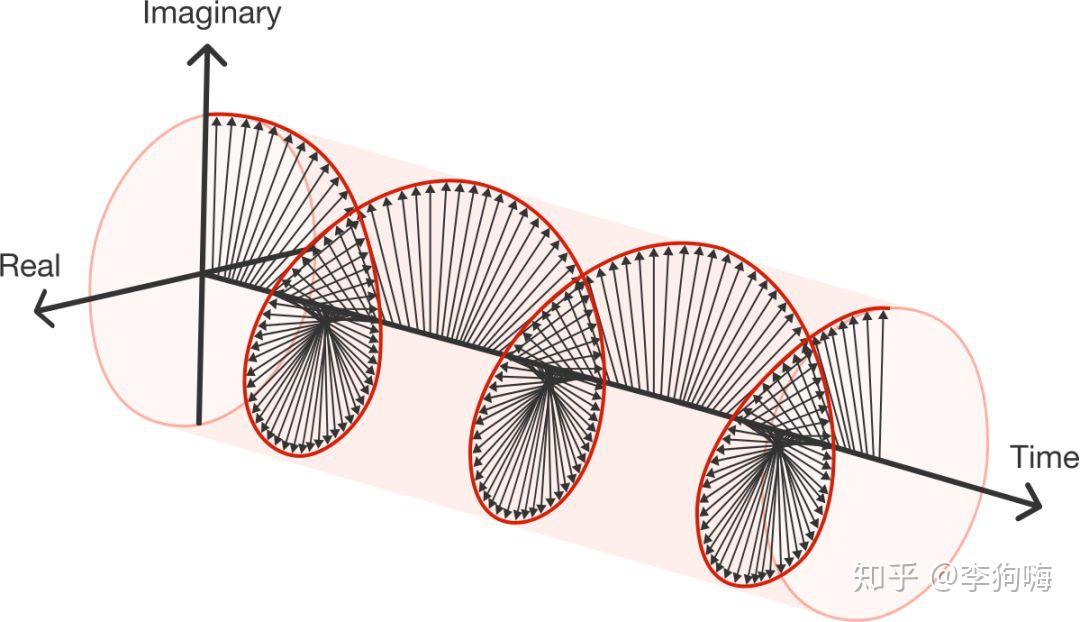（图片来源：Brilliant）

这里，只要令 ，就有 或者 .