参数估计

参数估计

10分钟掌握数理统计参数估计问题求解（考研、期末复习均可以用） - 爱学习的XP的文章 - 知乎 https://zhuanlan.zhihu.com/p/299600620

其实参数估计这部分内容，知识点不多，主要运用到的是数理统计基本概念中的三个分布进行求解，只要记住了三个分布的关系，以及几个常用统计量的分布（如下），那么在计算区间估计的时候直接用这些公式即可推导出来，没必要背太多的公式

开讲之前，先来看下参数估计方面的思维导图：

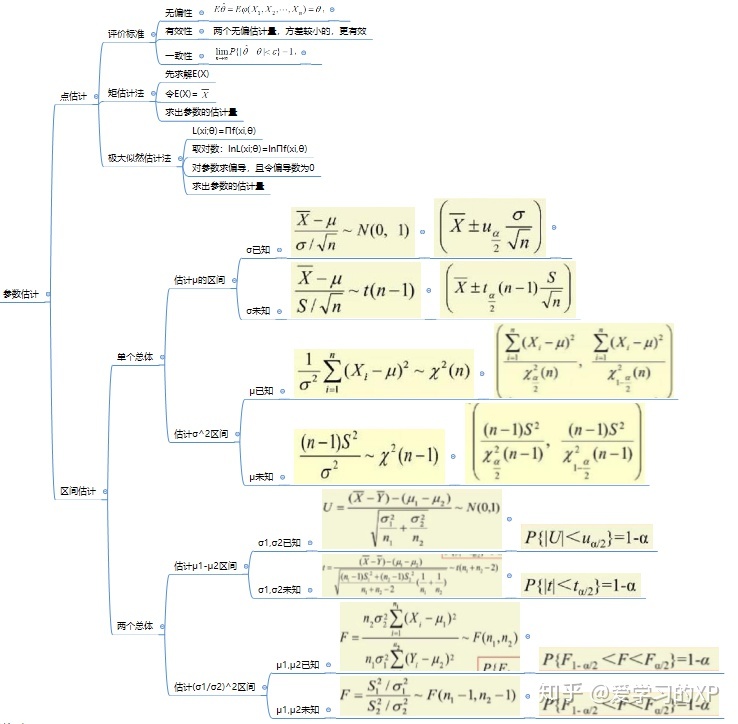
框架看完了，然后针对框架中的内容进行一一介绍

一、点估计

（一）估计量与评价标准

1、估计量

用统计量 来估计未知参数 ，称该统计量为参数的估计量

2、评价标准

（1）无偏性

若估计量 ，称估计量 为参数 的无偏估计

（2）有效性

设 与 都是参数 的无偏估计量，若 ，则称 比 更有效

（3）一致性

设 是参数 的估计量，若对任意的 ，有 ，称 为参数 的一致估计量

仅从上面几个进行了解评价标准，可能很多人看完会一脸懵逼，下面通过例题进行应用的讲解

【例题】

设总体 ~ ， 是来自总体的三个样本，判断估计量 ， 是否为 的无偏估计，若是，则判断哪个估计量更为有效？

解答：

首先判断无偏性，根据定义：


所以两个估计量均是 的无偏估计
再判断其有效性：


，所以 更为有效

2、求点估计量的两种方法

上述介绍了点估计量的几个评价标准，那么估计量怎么进行求解呢，书上介绍了两种方法：矩估计法和最大似然估计法，下面详细介绍（关于点估计的求解每年考研必考，请注意）

（1）矩估计法

矩估计法解法如下：

（a）求解
（b）另 ， ，
（c）根据上述式子即可求解出估计量
备注：一般来说，通过 即可解答出大部分的题目，如果解答不出再进行二次方的求解，无需一上来就求解二次方、三次方等

【例题1】

设总体 ~ ，求解参数 的矩估计量

解答：

，解答完毕

【例题2】

设总体 ~ ，求解参数 的矩估计量

解答：

，两个参数，一个方程，无法求解出 的估计量，因此需要继续往下进行求解

通过以上两个式子求解两个参数
，

（2）最大似然估计法

极大似然估计法可以简单理解为是参数能取得的极值估计，方法如下：

（a）设
（b）对函数取对数
（c）利用上述函数对 求偏导，并另偏导数为0，即
（d）根据上述式子即可求解出估计量
备注：在有的题目中 的取值恒大于0或小于0，则根据极值的判别法，当偏导数恒大于0时，说明随着 的增大，其函数值是增大的，所以 应取题目中所能取到的最大值作为估计量；相反的，当偏导数小于0时，应取题目中所能取到的最小值作为估计量

【例题1】

设总体 ~ ，求解参数 的最大似然估计量

解答：

因为偏导数小于0，所以函数随 增大而变小，故 应取最小值，即

【例题2】

设总体 ~ ，求解参数 的最大似然估计量

解答：

，求解完毕

二、区间估计

区间估计的计算主要是根据题目要求，设定相关的统计量，然后根据置信度求解出置信区间

1、置信区间

设总体的分布函数为 ，其中 为未知参数， 为来自总体 的简单样本，对给定的 ，若存在统计量 及 ，使得 ，称区间 为参数 的置信度为 的置信区间

关于统计量的设定，一般来说根据题目已知量和未知量进行判断，如下：

2、一个正态总体下的置信区间

上述对置信区间的描述有点过于复杂，下面举个例子进行讲解

【例题】

已知总体 ~ ， 已知，求解 在 下的置信区间

解答：

因为 已知，因此设统计量 ~
根据题意，
即
移项后可得

以上是 已知，求 的置信区间，另外还有其他几种置信区间的情况，具体如下：

以上几个参数的置信区间可以用假定的统计量进行推导而出，当然如果不想推导的同学们也可以直接进行背诵

3、两个正态总体下的置信区间

两个总体的置信区间及假设的统计量如下：