一、softmax loss

一、softmax loss

https://zhuanlan.zhihu.com/p/105722023

1.1 softmax

使用softmax作为激活函数的时候，一般使用交叉熵作为损失函数

Softmax Loss - 图1
1）将预测结果转化为非负数
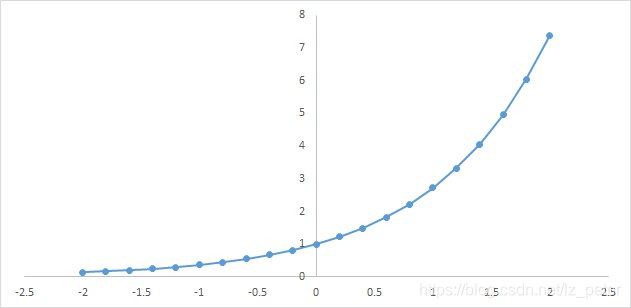
下图为y=exp(x）的图像，我们可以知道指数函数的值域取值范围是零到正无穷。softmax第一步就是将模型的预测结果转化到指数函数上，这样保证了概率的非负性。

引入指数函数的优点：

1.保证非负性
2.将数值结果距离拉大（y轴上变化剧烈）
3.求导方便

缺点：

y轴数值较大时，指数计算后的数值可能很大，数值会溢出

解决办法：将输出减去输出值中的最大值

Softmax Loss - 图2

2）各种预测结果概率之和等于1
为了确保各个预测结果的概率之和等于1。我们只需要将转换后的结果进行归一化处理。方法就是将转化后的结果除以所有转化后结果之和，可以理解为转化后结果占总数的百分比。这样就得到近似的概率。
下面为大家举一个例子，假如模型对一个三分类问题的预测结果为-3、1.5、2.7。我们要用softmax将模型结果转为概率。步骤如下：
1）将预测结果转化为非负数
y1 = exp(x1) = exp(-3) = 0.05
y2 = exp(x2) = exp(1.5) = 4.48
y3 = exp(x3) = exp(2.7) = 14.88
2）各种预测结果概率之和等于1
z1 = y1/(y1+y2+y3) = 0.05/(0.05+4.48+14.88) = 0.0026
z2 = y2/(y1+y2+y3) = 4.48/(0.05+4.48+14.88) = 0.2308
z3 = y3/(y1+y2+y3) = 14.88/(0.05+4.48+14.88) = 0.7666
总结一下softmax如何将多分类输出转换为概率，可以分为两步：
1）分子：通过指数函数，将实数输出映射到零到正无穷。
2）分母：将所有结果相加，进行归一化。

1.2 softmax 反向传播

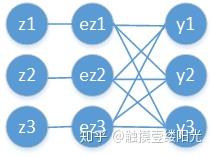
回顾Softmax函数的表达式，其中i表示输出节点的编号：
Softmax Loss - 图5 ，
影响 Softmax Loss - 图6 的有与之相连的 Softmax Loss - 图7 ，因此需要分别求出 Softmax Loss - 图8 。此时输出值 Softmax Loss - 图9 为 Softmax Loss - 图10 ，很明显 Softmax Loss - 图11 与 Softmax Loss - 图12 结果不同，而 Softmax Loss - 图13 只需换相应索引号即可。因此在对Softmax函数求导的时候，需要分两种情况考虑。即对第i个输出节点，分为对 Softmax Loss - 图14 的 Softmax Loss - 图15 求导以及其它 Softmax Loss - 图16 的 Softmax Loss - 图17 求导。

对时，类似前面介绍的 。Softmax函数的偏导数 可以展开为：

Softmax Loss - 图21
上面使用了函数相除的导数运算，由于是对 Softmax Loss - 图22 求导数，由于此时 Softmax Loss - 图23 ，因此 Softmax Loss - 图24 的导数还是 Softmax Loss - 图25 本身，对 Softmax Loss - 图26 求导结果只保留 Softmax Loss - 图27 。因此上面求导的结果为：
Softmax Loss - 图28
提取公共项 Softmax Loss - 图29 :
Softmax Loss - 图30
拆分成两个部分：
Softmax Loss - 图31
为了方便，将Softmax函数表达式 Softmax Loss - 图32 表示为 Softmax Loss - 图33 ，结果为 Softmax Loss - 图34 ，由于此时 Softmax Loss - 图35 ， Softmax Loss - 图36 ,因此最终结果为 Softmax Loss - 图37 。

对时，类似前面介绍的 或。Softmax函数的偏导数 可以展开为：

Softmax Loss - 图42
上面使用了函数相除的导数运算，由于是对 Softmax Loss - 图43 求导数，由于此时 Softmax Loss - 图44 ，因此 Softmax Loss - 图45 相当于常数，常数的导数为0，对 Softmax Loss - 图46 求导同样只保留 Softmax Loss - 图47 。因此上面求导的结果为：
Softmax Loss - 图48
分解两项相乘：
Softmax Loss - 图49
为了方便，将Softmax函数表达式 Softmax Loss - 图50 表示为 Softmax Loss - 图51 ，结果为 Softmax Loss - 图52 ，由于此时 Softmax Loss - 图53 ，因此最终结果为 Softmax Loss - 图54 。
对于Softmax函数的梯度推导依然使用的是导数的基本运算，并不复杂。最关键的是要对 Softmax Loss - 图55 以及 Softmax Loss - 图56 两种情况分别讨论。
偏导数的最终表达式如下：
Softmax Loss - 图57

1.3 softmax loss

接下来看一看Softmax的损失函数。回顾Softmax函数的表达式：
Softmax Loss - 图58
假设此时第i个输出节点为正确类别对应的输出节点，则 Softmax Loss - 图59 是正确类别对应输出节点的概率值。添加 Softmax Loss - 图60 运算不影响函数的单调性，首先为 Softmax Loss - 图61 添加 Softmax Loss - 图62 运算：
Softmax Loss - 图63
由于此时的 Softmax Loss - 图64 是正确类别对应的输出节点的概率，当然希望此时的 Softmax Loss - 图65 越大越好（当然最大不能超过1）。通常情况下使用梯度下降法来迭代求解，因此只需要为 Softmax Loss - 图66 加上一个负号变成损失函数，现在变成希望损失函数越小越好：
Softmax Loss - 图67
对上面的式子进一步处理：
Softmax Loss - 图68
这样就将上面的Softmax一步一步转换成了Softmax的损失函数。

1.4 交叉熵损失函数

Softmax Loss - 图69
对于分类任务来说，真实的样本标签通常表示为one-hot的形式。比如对于三分类来说，真实类别的索引位置为1，也就是属于第二个类别，那么使用one-hot编码表示为[0, 1, 0]，也就是仅正确类别位置为1，其余位置都为0。而式子2中的 Softmax Loss - 图70 就是真实样本的标签值，将[0, 1, 0]代入式子2中即： Softmax Loss - 图71
最终的结果为 Softmax Loss - 图72
softmax loss 和交叉熵loss的区别在于，softmax是对正确类别的损失，二交叉熵是对所有类别的损失
Softmax Loss - 图73

1.5 交叉熵损失函数反向传播

最终损失函数 Softmax Loss - 图74 对网络输出变量 Softmax Loss - 图75 的偏导数，展开为：
Softmax Loss - 图76
接下来利用复合函数分解成：
Softmax Loss - 图77
Softmax Loss - 图78 ，其中 Softmax Loss - 图79 就是我们前面推导的Softmax函数的偏导数。
对于Softmax函数分为两种情况，因此需要将求和符号拆分成 Softmax Loss - 图80 以及 Softmax Loss - 图81 这两种情况，代入 Softmax Loss - 图82 求解公式，可得：
Softmax Loss - 图83
进一步进一步化简为：
Softmax Loss - 图84
提取公共项 Softmax Loss - 图85 ，可得：
Softmax Loss - 图86
至此完成了对交叉熵函数的梯度推导。对于分类问题中标签y通过one-hot编码的方式，则有如下关系：
Softmax Loss - 图87
因此将交叉熵的偏导数进一步简化为：
Softmax Loss - 图88