反向传播

原文
梯度下降可以应对带有明确求导函数的情况，或者说可以应对那些可以求出误差的情况，比如逻辑回归（Logistic Regression），我们可以把它看做没有隐层的网络；但对于多隐层的神经网络，输出层可以直接求出误差来更新参数，但其中隐层的误差是不存在的，因此不能对它直接应用梯度下降，而是先将误差反向传播至隐层，然后再应用梯度下降，其中将误差从末层往前传递的过程需要链式法则（Chain Rule）的帮助，因此反向传播算法可以说是梯度下降在链式法则中的应用。

1. 前向传播

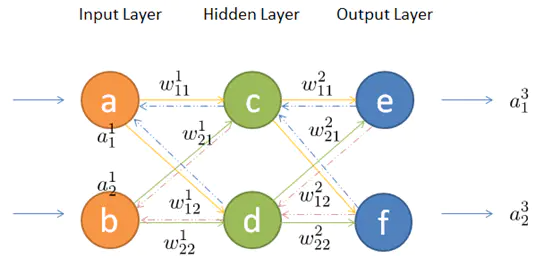
第二层神经元的输入（即第一层神经元的输出），为 输入 X 权重 + 偏置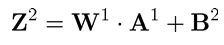

经过激活函数引入非线性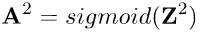

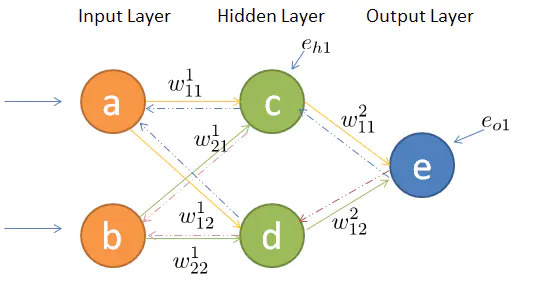
2. 反向传播

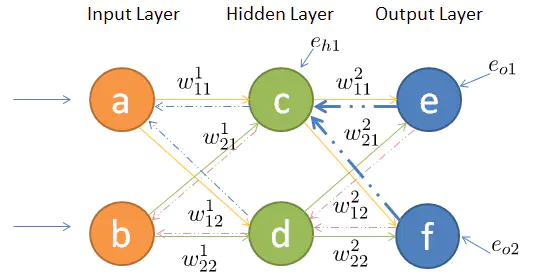
隐藏层的误差为输出误差在该层的权重。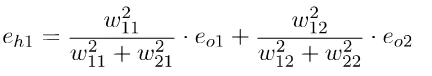


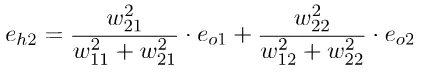
矩阵表示：

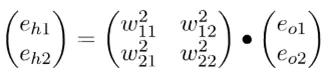
实际为权重矩阵的转置

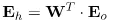
3.链式求导

a1为输出值，y1为真实值

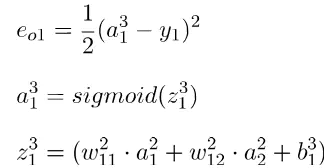
误差对w11求偏导如下：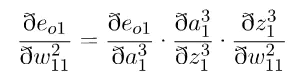

=

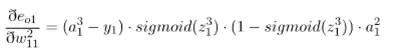
误差对于w12的偏导如下：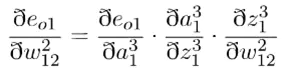

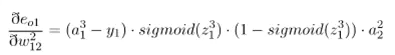
误差对于偏置求偏导如下：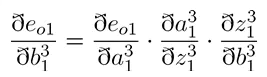

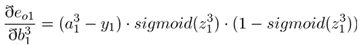
求出偏导数后带入全职更新公式即可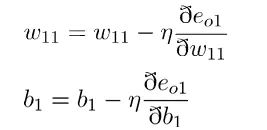

输出层的误差可以表示为（上图红色框公式）：

隐藏层的误差可以表示为（上图蓝色框公式）

权重更新的表示为（上图绿色框公式）：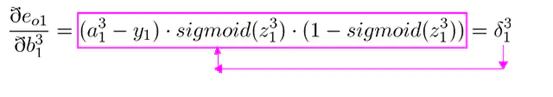

对于偏置的更新表示为（上图红色框）：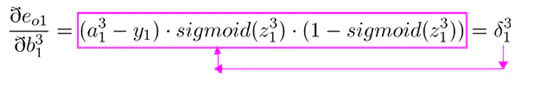

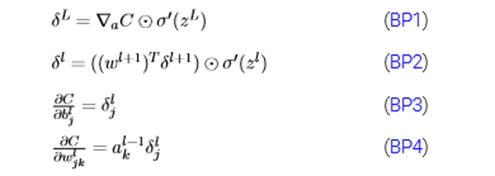
由bp2可知，第二层的误差为第三层的误差乘以权值矩阵的转置点乘当前层的输入