K-means 是我们最常用的基于欧式距离的聚类算法，其认为两个目标的距离越近，相似度越大。无监督学习

1. 算法步骤

K-means 的算法步骤为：

选择初始化的 k 个样本作为初始聚类中心；
针对数据集中每个样本计算它到 k 个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中；
针对每个类别，重新计算它的聚类中心（即属于该类的所有样本的质心）；
重复上面 2 3 两步操作，直到达到某个中止条件（迭代次数、最小误差变化等）。
2. 复杂度
伪代码：
```
获取数据 n 个 m 维的数据
随机生成 K 个 m 维的点
while(t)
 for(int i=0;i < n;i++)
     for(int j=0;j < k;j++)
         计算点 i 到类 j 的距离
 for(int i=0;i < k;i++)
     1. 找出属于自己这一类的所有数据点
     2. 把自己的坐标修改为这些数据点的中心点坐标
end
```
时间复杂度：，其中，t 为迭代次数，k 为簇的数目，n 为样本点数，m 为样本点维度。
空间复杂度：，其中，k 为簇的数目，m 为样本点维度，n 为样本点数。
3.优缺点
3.1 优点

容易理解，聚类效果不错,收敛速度快
处理大数据集的时候，该算法可以保证较好的伸缩性；
当簇近似高斯分布的时候，效果非常不错；
算法复杂度低。

3.2 缺点
K 值需要人为设定，不同 K 值得到的结果不一样；
对初始的簇中心敏感，不同选取方式会得到不同结果；
对异常值敏感；
样本只能归为一类，不适合多分类任务；
不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。
4.K-Means初始化优化K-Means++
选择合适的k个质心。
如果仅仅是完全随机的选择，有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法的优化。
K-Means++的对于初始化质心的优化策略也很简单，如下：
a) 从输入的数据点集合中随机选择一个点作为第一个聚类中心μ1μ1
b) 对于数据集中的每一个点xi，计算它与已选择的聚类中心中最近聚类中心的距离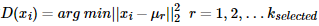
c) 选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)D(x)较大的点，被选取作为聚类中心的概率较大
d) 重复b和c直到选择出k个聚类质心
5. K-Means距离计算优化elkan K-Means
在传统的K-Means算法中，我们在每轮迭代时，要计算所有的样本点到所有的质心的距离，这样会比较的耗时。那么，对于距离的计算有没有能够简化的地方呢？elkan K-Means算法就是从这块入手加以改进。它的目标是减少不必要的距离的计算。那么哪些距离不需要计算呢？
elkan K-Means利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质，来减少距离的计算。
第一种规律是对于一个样本点x和两个质心。如果我们预先计算出了这两个质心之间的距离D(j1,j2)，则如果计算发现2D(x,j1)≤D(j1,j2),我们立即就可以知道D(x,j1)≤D(x,j2)。此时我们不需要再计算D(x,j2),也就是说省了一步距离计算。
第二种规律是对于一个样本点xx和两个质心。我们可以得到D(x,j2)≥max{0,D(x,j1)−D(j1,j2)}。这个从三角形的性质也很容易得到。
利用上边的两个规律，elkan K-Means比起传统的K-Means迭代速度有很大的提高。但是如果我们的样本的特征是稀疏的，有缺失值的话，这个方法就不使用了，此时某些距离无法计算，则不能使用该算法。

CV知识点

K-means总结

1. 算法步骤

2. 复杂度

3.优缺点

3.1 优点

3.2 缺点

4.K-Means初始化优化K-Means++

5. K-Means距离计算优化elkan K-Means