复杂度分析

复杂度分析法

算法的执行效率，粗略地讲就是算法代码执行的时间。

时间复杂度分析

大O复杂度表示法

公式：

T(n)：代码执行的时间
n：表示数据规模的大小
f(n)：表示每行代码执行的次数总和
O：表示代码的执行时间T(n)与f(n)表达式成正比
大O时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，也叫渐进时间复杂度，简称时间复杂度。
由于大O复杂度表示方法只是表示一种变化趋势，通常会忽略掉公式中的常量、低阶、系数，只需记录一个最大阶的量级就可以了。可以采用以下三种方式进行分析

分析方法：

• 1、只需关注循环执行次数最多的一段代码
• 2、加法法则：总复杂度等于量级最大的那段代码的复杂度

• 3、乘法法则：嵌套代码的复杂度登录嵌套内外代码复杂度的乘机

  复杂度量级(按数量级递增)

• 常量阶：

• 对数阶：
• 线性阶：
• 线性对数阶段：
• 平方阶：
• 指数阶：
• 阶乘阶：

空间复杂度分析

空间复杂度全称为渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系。
空间复杂度通常只有以下度量级

• 常量阶：
• 线性阶：
• 平方阶：

度量级趋势图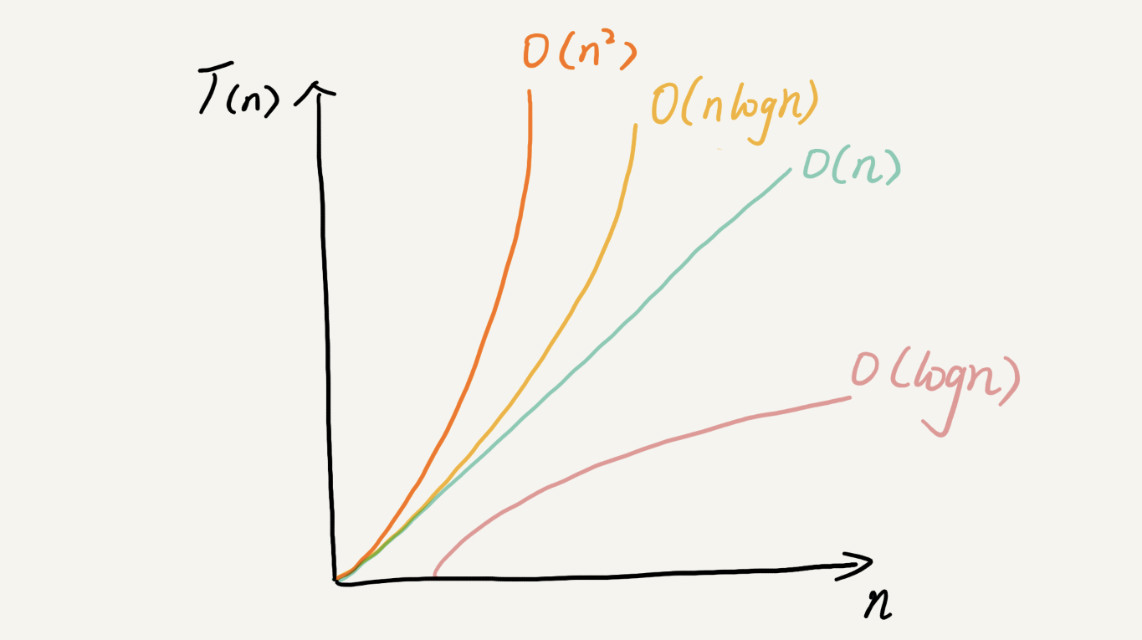

参考极客时间：https://time.geekbang.org/column/intro/100017301