过滤法通过使用一些统计量或假设检验结果为每个变量打分。得分较高的功能往往更加重要，因此应被包含在子集中。以下为一个简单的基于过滤法的机器学习工作流（以最简单的训练-验证-测试这种数据集划分方法为例）。 过滤法（单变量） - 图1

单变量特征过滤

单变量过滤方法（Univariate Filter Methods）依据单变量统计量或统计检验选择最佳特征。其仅仅考虑单个变量与目标变量的关系（方差选择法仅基于单个变量）。

方差选择法

方差选择法删除变量方差低于某个阈值的所有特征。默认情况下是删除方差为零的特征（所有观测点中具有相同值的特征），因为该特征无法解释目标变量的任何变化。
假设我们有一个特征是由0和1组成的数据集，移除那些在整个数据集中特征值为0或者为1的比例超过p（同一类样本所占的比例）的特征。0 1 组成的数据集满足伯努利（ Bernoulli ）分布，因此其特征变量的方差为：p(1-p)。
在sklearn中的VarianceThreshold可以让和我们快速完成这个操作

  1. import numpy as np
  2. import pandas as pd
  3. from sklearn.feature_selection import VarianceThreshold
  5. # 合成一些数据集用于演示
  6. train_set = np.array([[1,2,3],[1,4,7],[1,4,9]]) # 可见第一个变量方差为0
  7. # array([[1, 2, 3],
  8. #        [1, 4, 7],
  9. #        [1, 4, 9]])
  11. test_set = np.array([[3,2,3],[1,2,7]]) # 故意将第二个变量方差设为0
  12. # array([[3, 2, 3],
  13. #        [1, 2, 7]])
  15. selector = VarianceThreshold()
  16. selector.fit(train_set) # 在训练集上训练
  17. transformed_train = selector.transform(train_set) # 转换训练集,这里的transform就是将我们的模型运用的我们要处理的数据上,类似predict
  18. # 下面为返回结果，可见第一个变量已被删除
  19. # array([[2, 3],
  20. #        [4, 7],
  21. #        [4, 9]])
  23. transformed_test = selector.transform(test_set) # 转换测试集
  24. # 下面为返回结果，可见第一个变量已被删除
  25. # array([[2, 3],
  26. #        [2, 7]])
  27. # 虽然测试集中第二个变量的方差也为0
  28. # 但是我们的选择是基于训练集，所以我们依然删除第一个变量


皮尔森相关系数

皮尔森相关系数一般用于衡量两个连续变量之间的线性相关性，也可以用于衡量二元变量与目标变量的相关性。故可以将类别变量利用独热编码转换为多个二元变量之后利用皮尔森相关系数进行筛选。这里的操作和相关矩阵是一样的。
sklearn中的SelectKBest可以帮助我们快速完成这操作，下面的代码很长，在pandas中用df.corr()就可以完成相关系数的计算。

  1. import numpy as np
  2. from scipy.stats import pearsonr
  3. from sklearn.feature_selection import SelectKBest
  5. # 直接载入数据集
  6. from sklearn.datasets import fetch_california_housing
  7. dataset = fetch_california_housing()
  8. X, y = dataset.data, dataset.target # 利用 california_housing 数据集来演示
  9. # 此数据集中，X，y均为连续变量，故此满足使用皮尔森相关系数的条件
  11. # 选择前15000个观测点作为训练集
  12. # 剩下的作为测试集
  13. train_set = X[0:15000,:]
  14. test_set = X[15000:,]
  15. train_y = y[0:15000]
  17. # sklearn 中没有直接的方程可以使用
  18. # 此处将用 scipy.stats.pearsonr方程来实现基于皮尔森相关系数的特征过滤
  19. # 注意 scipy.stats.pearsonr 计算的是两个变量之间的相关系数
  20. # 因sklearn SelectKBest需要，我们将基于scipy.stats.pearsonr 重写允许多特征同时输入的方程 udf_pearsonr
  22. def udf_pearsonr(X, y):
  23.     # 将会分别计算每一个变量与目标变量的关系
  24.     result = np.array([pearsonr(x, y) for x in X.T]) # 包含(皮尔森相关系数, p值) 的列表
  25.     return np.absolute(result[:,0]), result[:,1]
  27. # SelectKBest 将会基于一个判别方程自动选择得分高的变量
  28. # 这里的判别方程为皮尔森相关系数
  29. selector = SelectKBest(udf_pearsonr, k=2) # k => 我们想要选择的变量数
  30. selector.fit(train_set, train_y) # 在训练集上训练
  31. transformed_train = selector.transform(train_set) # 转换训练集
  32. transformed_train.shape #(15000, 2), 其选择了第一个及第七个变量 
  33. assert np.array_equal(transformed_train, train_set[:,[0,6]])
  35. transformed_test = selector.transform(test_set) # 转换测试集
  36. assert np.array_equal(transformed_test, test_set[:,[0,6]]);
  37. # 可见对于测试集，其依然选择了第一个及第七个变量
# 验算一下我们的结果
for idx in range(train_set.shape[1]):
    pea_score, p_value = pearsonr(train_set[:,idx], train_y)
    print(f"第{idx + 1}个变量和目标的皮尔森相关系数的绝对值为{round(np.abs(pea_score),2)}, p-值为{round(p_value,3)}")
# 应选择第一个及第七个变量

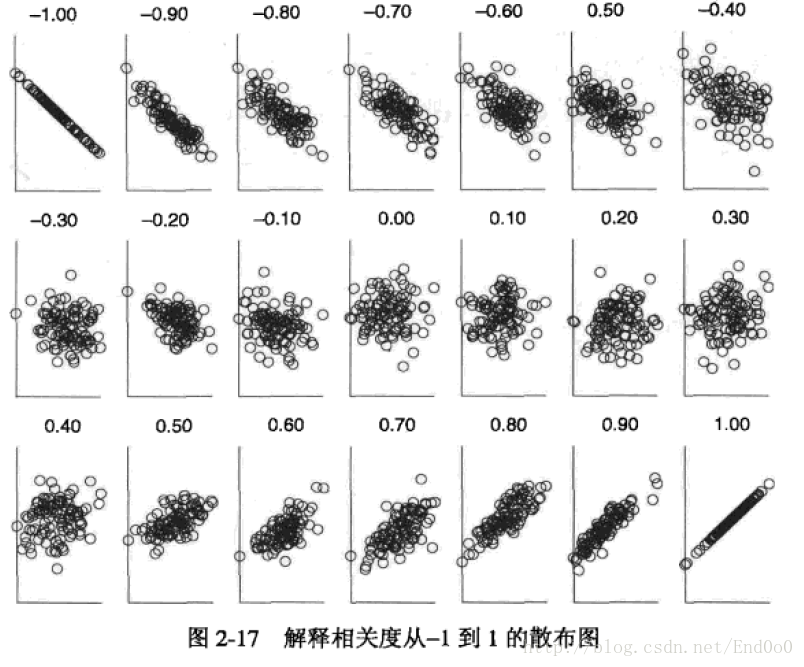
过滤法（单变量） - 图2

距离相关系数（回归）

距离相关系数（Distance Correlation）一般用来回归问题上，与皮尔森相关系数类似，距离相关系数也一般被用于衡量两个连续变量之间的相关性。但与皮尔森相关系数不同的是，距离相关系数还衡量了两个变量之间的非线性关联。

import numpy as np
from dcor import distance_correlation
from dcor.independence import distance_covariance_test
from sklearn.feature_selection import SelectKBest

# 直接载入数据集
from sklearn.datasets import fetch_california_housing
dataset = fetch_california_housing()
X, y = dataset.data, dataset.target # 利用 california_housing 数据集来演示
# 此数据集中，X，y均为连续变量，故此满足使用距离相关系数的条件

# 选择前15000个观测点作为训练集
# 剩下的作为测试集
train_set = X[0:15000,:]
test_set = X[15000:,]
train_y = y[0:15000]

# sklearn 中没有直接的方程可以使用
# 此处将用 dcor.distance_correlation方程来实现基于距离相关系数的特征过滤
# 注意 dcor.distance_correlation 计算的是两个变量之间的相关系数
# 因sklearn SelectKBest需要，我们将基于dcor.distance_correlation 重写允许多特征同时输入的方程 udf_dcorr

def udf_dcorr(X, y):
    # 将会分别计算每一个变量与目标变量的关系
    result = np.array([[distance_correlation(x, y), 
                        distance_covariance_test(x,y)[0]]for x in X.T]) # 包含(距离相关系数, p值) 的列表
    return result[:,0], result[:,1]

# SelectKBest 将会基于一个判别方程自动选择得分高的变量
# 这里的判别方程为距离相关系数
selector = SelectKBest(udf_dcorr, k=2) # k => 我们想要选择的变量数
selector.fit(train_set, train_y) # 在训练集上训练
transformed_train = selector.transform(train_set) # 转换训练集
transformed_train.shape #(15000, 2), 其选择了第一个及第三个变量 
assert np.array_equal(transformed_train, train_set[:,[0,2]])

transformed_test = selector.transform(test_set) # 转换测试集
assert np.array_equal(transformed_test, test_set[:,[0,2]]);
# 可见对于测试集，其依然选择了第一个及第三个变量

# 验算一下我们的结果
for idx in range(train_set.shape[1]):
    d_score = distance_correlation(train_set[:,idx], train_y)
    p_value = distance_covariance_test(train_set[:,idx], train_y)[0]
    print(f"第{idx + 1}个变量和目标的距离相关系数为{round(d_score,2)}, p-值为{round(p_value,3)}")
# 应选择第一个及第三个变量

F统计量（回归）

F统计量（F-Score）用于检验线性回归模型的整体显著性。在sklearn中，其将对每一个变量分别建立一个一元的线性回归模型，然后分别报告每一个对应模型的F统计量。F-统计量的零假设是该线性模型系数不显著，在一元模型中，该统计量能够反映各变量与目标变量之间的线性关系。因此，我们应该选择具有较高F统计量的特征（更有可能拒绝原假设）。

import numpy as np
from sklearn.feature_selection import f_regression
from sklearn.feature_selection import SelectKBest

# 直接载入数据集
from sklearn.datasets import fetch_california_housing
dataset = fetch_california_housing()
X, y = dataset.data, dataset.target # 利用 california_housing 数据集来演示
# 此数据集中，X，y均为连续变量，故此满足使用F统计量的条件

# 选择前15000个观测点作为训练集
# 剩下的作为测试集
train_set = X[0:15000,:]
test_set = X[15000:,]
train_y = y[0:15000]

# sklearn 中直接提供了方程用于计算F统计量
# SelectKBest 将会基于一个判别方程自动选择得分高的变量
# 这里的判别方程为F统计量
selector = SelectKBest(f_regression, k=2) # k => 我们想要选择的变量数
selector.fit(train_set, train_y) # 在训练集上训练
transformed_train = selector.transform(train_set) # 转换训练集
transformed_train.shape #(15000, 2), 其选择了第一个及第七个变量 
assert np.array_equal(transformed_train, train_set[:,[0,6]])

transformed_test = selector.transform(test_set) # 转换测试集
assert np.array_equal(transformed_test, test_set[:,[0,6]]);
# 可见对于测试集，其依然选择了第一个及第七个变量

# 验算一下我们的结果
for idx in range(train_set.shape[1]):
    score, p_value = f_regression(train_set[:,idx].reshape(-1,1), train_y)
    print(f"第{idx + 1}个变量的F统计量为{round(score[0],2)}, p-值为{round(p_value[0],3)}")
# 故应选择第一个及第七个变量

互信息（回归）

互信息（Mutual Information）衡量变量间的相互依赖性。其本质为熵差，即知道另一个变量信息后混乱的降低程度 。当且仅当两个随机变量独立时MI等于零。MI值越高，两变量之间的相关性则越强。与Pearson相关和F统计量相比，它还捕获了非线性关系。
实际运用中，一种极有可能的情况是，x和y中的一个可能是离散变量，而另一个是连续变量。因此sklearn中，采用的是基于k最临近算法的熵估计非参数方法

import numpy as np
from sklearn.feature_selection import mutual_info_regression
from sklearn.feature_selection import SelectKBest

# 直接载入数据集
from sklearn.datasets import fetch_california_housing
dataset = fetch_california_housing()
X, y = dataset.data, dataset.target # 利用 california_housing 数据集来演示
# 此数据集中，X，y均为连续变量，故此满足使用MI的条件

# 选择前15000个观测点作为训练集
# 剩下的作为测试集
train_set = X[0:15000,:].astype(float)
test_set = X[15000:,].astype(float)
train_y = y[0:15000].astype(float)

# KNN中的临近数是一个非常重要的参数
# 故我们重写了一个新的MI计算方程更好的来控制这一参数
def udf_MI(X, y):
    result = mutual_info_regression(X, y, n_neighbors = 5) # 用户可以输入想要的临近数
    return result

# SelectKBest 将会基于一个判别方程自动选择得分高的变量
# 这里的判别方程为F统计量
selector = SelectKBest(udf_MI, k=2) # k => 我们想要选择的变量数
selector.fit(train_set, train_y) # 在训练集上训练
transformed_train = selector.transform(train_set) # 转换训练集
transformed_train.shape #(15000, 2), 其选择了第一个及第八个变量
assert np.array_equal(transformed_train, train_set[:,[0,7]])

transformed_test = selector.transform(test_set) # 转换测试集
assert np.array_equal(transformed_test, test_set[:,[0,7]]);
# 可见对于测试集，其依然选择了第一个及第八个变量

# 验算上述结果
for idx in range(train_set.shape[1]):
    score = mutual_info_regression(train_set[:,idx].reshape(-1,1), train_y, n_neighbors = 5)
    print(f"第{idx + 1}个变量与因变量的互信息为{round(score[0],2)}")
# 故应选择第一个及第八个变量

卡方统计量

卡方统计量主要用于衡量两个类别特征之间的相关性。sklearn提供了chi2方程用于计算卡方统计量。其输入的特征变量必须为布尔值或频率（故对于类别变量应考虑独热编码）。卡方统计量的零假设为两个变量是独立的，因为卡方统计量值越高，则两个类别变量的相关性越强。因此，我们应该选择具有较高卡方统计量的特征。

在sklearn中利用chi2计算出来的卡方统计量并不是统计意义上的卡方统计量。当输入变量为布尔变量时，chi2计算值为该布尔变量为True时候的卡方统计量（我们将会在下文举例说明）。这样的优势是，独热编码生成的所有布尔值变量的chi2值之和将等于原始变量统计意义上的卡方统计量。

举个简单的例子，假设一个变量I有0，1，2两种可能的值，则独特编码后一共会产生3个新的布尔值变量。这三个布尔值变量的chi2计算出来的值之和，将等于变量I与因变量直接计算得出的统计意义上的卡方统计量。

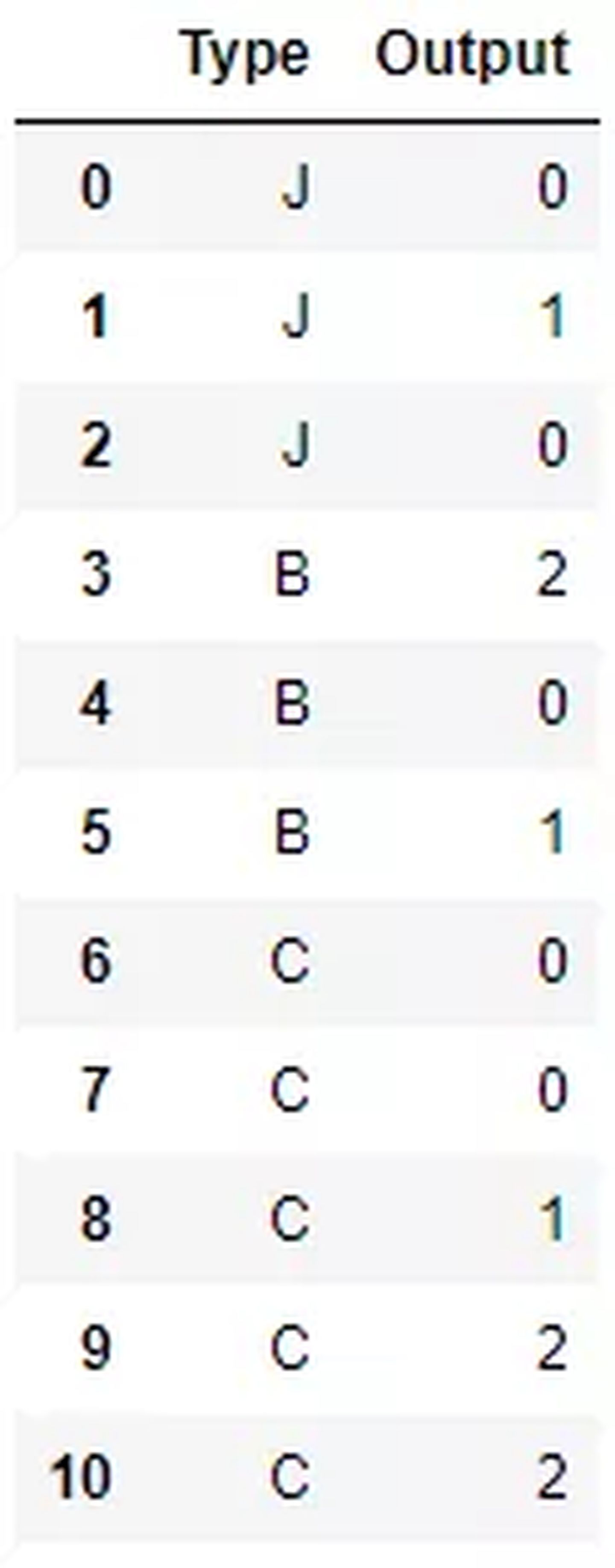
import pandas as pd
sample_dict = {'Type': ['J','J','J',
                        'B','B','B',
                        'C','C','C','C','C'], 
               'Output': [0, 1, 0, 
                          2, 0, 1,  
                          0, 0, 1, 2, 2,]}
sample_raw = pd.DataFrame(sample_dict)
sample_raw #原始数据，Output是我们的目标变量，Type为类别变量

过滤法（单变量） - 图3

# 下面利用独热编码生成布尔变量，并利用sklearn计算每一个布尔变量的chi2值
sample = pd.get_dummies(sample_raw)
from sklearn.feature_selection import chi2
chi2(sample.values[:,[1,2,3]],sample.values[:,[0]])
# 第一行为每一个布尔变量的chi2值

输出：
_(array([0.17777778, 0.42666667, 1.15555556]),_
_array([0.91494723, 0.8078868 , 0.56114397]))_

# 下面直接计算原始变量Type与output统计学意义上的卡方统计量
# 首先，先统计每一个类别下出现的观测数，用于创建列联表
obs_df = sample_raw.groupby(['Type','Output']).size().reset_index()
obs_df.columns = ['Type','Output','Count']
obs_df

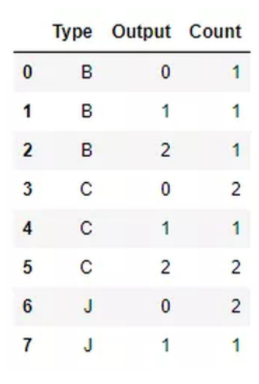image.png即列联表（contingency table）为：image.png

from scipy.stats import chi2_contingency
obs = np.array([[1, 1, 1], [2, 1, 2],[2, 1, 0]])
chi2_contingency(obs) # 第一个值即为变量Type与output统计学意义上的卡方统计量

输出：
_(1.7600000000000002,0.779791873961373,4,_
_array([[1.36363636, 0.81818182, 0.81818182], [2.27272727, 1.36363636, 1.36363636], [1.36363636, 0.81818182, 0.81818182]]))_
_

# 而chi2方程算出来的布尔值之和为即为原始变量的统计意义上的卡方统计量
chi2(sample.values[:,[1,2,3]],sample.values[:,[0]])[0].sum() == chi2_contingency(obs)[0]

输出：True

# 那么sklearn中的chi2是如何计算的呢？
# 不妨以第一个生成的布尔值为例，即Type为B
# chi2出来的值为0.17777778
# 而这与利用scipy以下代码计算出的计算一致
from scipy.stats import chisquare
f_exp = np.array([5/11, 3/11, 3/11]) * 3 # 预期频数为 output的先验概率 * Type为B 的样本数
chisquare([1,1,1], f_exp=f_exp) # [1,1,1] 即Type为B 的样本实际频数
# 即sklearn 中的chi2 仅考虑了Type为B情形下的列连表

输出：
Power_divergenceResult(statistic=0.17777777777777778,pvalue=0.9149472287300311)

import numpy as np
from sklearn.feature_selection import chi2
from sklearn.feature_selection import SelectKBest

# 直接载入数据集
from sklearn.datasets import load_iris # 利用iris数据作为演示数据集
iris = load_iris()
X, y = iris.data, iris.target
# 此数据集中，X为连续变量，y为类别变量
# 不满足chi2的使用条件

# 将连续变量变为布尔值变量以满足chi2使用条件
# 不妨利用其是否大于均值来生成布尔值（仅作为演示用）
X = X > X.mean(0)

# iris 数据集使用前需要被打乱顺序
np.random.seed(1234)
idx = np.random.permutation(len(X))
X = X[idx]
y = y[idx]

# 选择前100个观测点作为训练集
# 剩下的作为测试集
train_set = X[0:100,:]
test_set = X[100:,]
train_y = y[0:100]

# sklearn 中直接提供了方程用于计算卡方统计量
# SelectKBest 将会基于一个判别方程自动选择得分高的变量
# 这里的判别方程为F统计量
selector = SelectKBest(chi2, k=2) # k => 我们想要选择的变量数
selector.fit(train_set, train_y) # 在训练集上训练
transformed_train = selector.transform(train_set) # 转换训练集
transformed_train.shape #(100, 2), 其选择了第三个及第四个变量 
assert np.array_equal(transformed_train, train_set[:,[2,3]])

transformed_test = selector.transform(test_set) # 转换测试集
assert np.array_equal(transformed_test, test_set[:,[2,3]]);
# 可见对于测试集，其依然选择了第三个及第四个变量

# 验证上述结果
for idx in range(train_set.shape[1]):
    score, p_value = chi2(train_set[:,idx].reshape(-1,1), train_y)
    print(f"第{idx + 1}个变量与因变量的卡方统计量为{round(score[0],2)}，p值为{round(p_value[0],3)}")
# 故应选择第三个及第四个变量

F统计量（分类）

在分类机器学习问题中，若变量特征为类别特征，则我们可以使用独热编码配合上述chi2方法选择最重要的特征。但若特征为连续变量，则我们可以使用ANOVA-F值。ANOVA F统计量的零假设是若按目标变量（类别）分组，则连续变量的总体均值是相同的。故我们应选择具有高ANOVA-F统计量的连续变量，因为这些连续变量与目标变量的关联性强。

import numpy as np
from sklearn.feature_selection import f_classif
from sklearn.feature_selection import SelectKBest

# 直接载入数据集
from sklearn.datasets import load_iris # 利用iris数据作为演示数据集
iris = load_iris()
X, y = iris.data, iris.target
# 此数据集中，X为连续变量，y为类别变量
# 满足ANOVA-F的使用条件

# iris 数据集使用前需要被打乱顺序
np.random.seed(1234)
idx = np.random.permutation(len(X))
X = X[idx]
y = y[idx]

# 选择前100个观测点作为训练集
# 剩下的作为测试集
train_set = X[0:100,:]
test_set = X[100:,]
train_y = y[0:100]

# sklearn 中直接提供了方程用于计算ANOVA-F
# SelectKBest 将会基于一个判别方程自动选择得分高的变量
# 这里的判别方程为F统计量
selector = SelectKBest(f_classif, k=2) # k => 我们想要选择的变量数
selector.fit(train_set, train_y) # 在训练集上训练
transformed_train = selector.transform(train_set) # 转换训练集
transformed_train.shape #(100, 2), 其选择了第三个及第四个变量 
assert np.array_equal(transformed_train, train_set[:,[2,3]])

transformed_test = selector.transform(test_set) # 转换测试集
assert np.array_equal(transformed_test, test_set[:,[2,3]]);
# 可见对于测试集，其依然选择了第三个及第四个变量

# 验证上述结果
for idx in range(train_set.shape[1]):
    score, p_value = f_classif(train_set[:,idx].reshape(-1,1), train_y)
    print(f"第{idx + 1}个变量与因变量的ANOVA-F统计量为{round(score[0],2)}，p值为{round(p_value[0],3)}")
# 故应选择第三个及第四个变量

互信息（分类）

import numpy as np
from sklearn.feature_selection import mutual_info_classif
from sklearn.feature_selection import SelectKBest

# 直接载入数据集
from sklearn.datasets import load_iris # 利用iris数据作为演示数据集
iris = load_iris()
X, y = iris.data, iris.target
# 此数据集中，X为连续变量，y为类别变量
# 满足MI的使用条件

# iris 数据集使用前需要被打乱顺序
np.random.seed(1234)
idx = np.random.permutation(len(X))
X = X[idx]
y = y[idx]

# 选择前100个观测点作为训练集
# 剩下的作为测试集
train_set = X[0:100,:]
test_set = X[100:,]
train_y = y[0:100]

# KNN中的临近数是一个非常重要的参数
# 故我们重写了一个新的MI计算方程更好的来控制这一参数
def udf_MI(X, y):
    result = mutual_info_classif(X, y, n_neighbors = 5) # 用户可以输入想要的临近数
    return result

# SelectKBest 将会基于一个判别方程自动选择得分高的变量
# 这里的判别方程为F统计量
selector = SelectKBest(udf_MI, k=2) # k => 我们想要选择的变量数
selector.fit(train_set, train_y) # 在训练集上训练
transformed_train = selector.transform(train_set) # 转换训练集
transformed_train.shape #(100, 2), 其选择了第三个及第四个变量 
assert np.array_equal(transformed_train, train_set[:,[2,3]])

transformed_test = selector.transform(test_set) # 转换测试集
assert np.array_equal(transformed_test, test_set[:,[2,3]]);
# 可见对于测试集，其依然选择了第三个及第四个变量

# 验算上述结果
for idx in range(train_set.shape[1]):
    score = mutual_info_classif(train_set[:,idx].reshape(-1,1), train_y, n_neighbors = 5)
    print(f"第{idx + 1}个变量与因变量的互信息为{round(score[0],2)}")
# 故应选择第三个及第四个变量