复杂度概念

  • 链表主要是为了解决数组中的key发生hash冲突时，将发生碰撞的key存到链表中，红黑树主要是为了解决链表过长，的查询速度太慢问题，链表查询时间复杂度为O(n)，当链表长度大于等于8时，就会转变成红黑树，时间复杂度为O(logn)，当链表长度小于等于6时，由红黑树转变回链表，因为链表过短时引入红黑树反而会降低查询速度
  • 红黑树： 二叉树随机的话很正常（o(logn)）；如果时递增递减数据的话，就成了一个单向链表了(o(n))；所以出现了一个平衡二叉树，插入删除的时候效率虽然效率低于（o(logn)）；但是查找的时候数据仍然是（o(n)），保证了后续的效率了；（红黑树属于平衡二叉树，但是为了保持“平衡”是需要付出代价的，但是该代价所损耗的资源要比遍历线性链表要少）
    • 1 每个节点非红即黑
    • 2 根节点总是黑色的
    • 3 如果节点是红色的，则它的子节点必须是黑色的（反之不一定）
    • 4 每个叶子节点都是黑色的空节点（NIL节点）
    • 5从根节点到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点（即相同的黑色高度）、

自平衡的二叉树树的规则
左子树 与 右子树 的深度差不能大于1 ; 这就是自平衡的最大规则;
红黑树的规则

  1. 根节点必须是 黑色
  2. 叶子节点(包括null节点) 必须是 黑色 ( 导致:整个树中一半以上都是黑色的)
  3. 红色节点的子节点必须是 黑色
  4. 新插入节点 为红色,但是稍后会根据上述规则重新调整整棵树的结构
  5. 从任意节点到叶子节点的每条路径,必须包含相同数据的黑色节点;

(这个规则在非常极端的情况话,会出现一种现象;即:红黑树限定左侧树 与右侧树深度限定在两倍之内)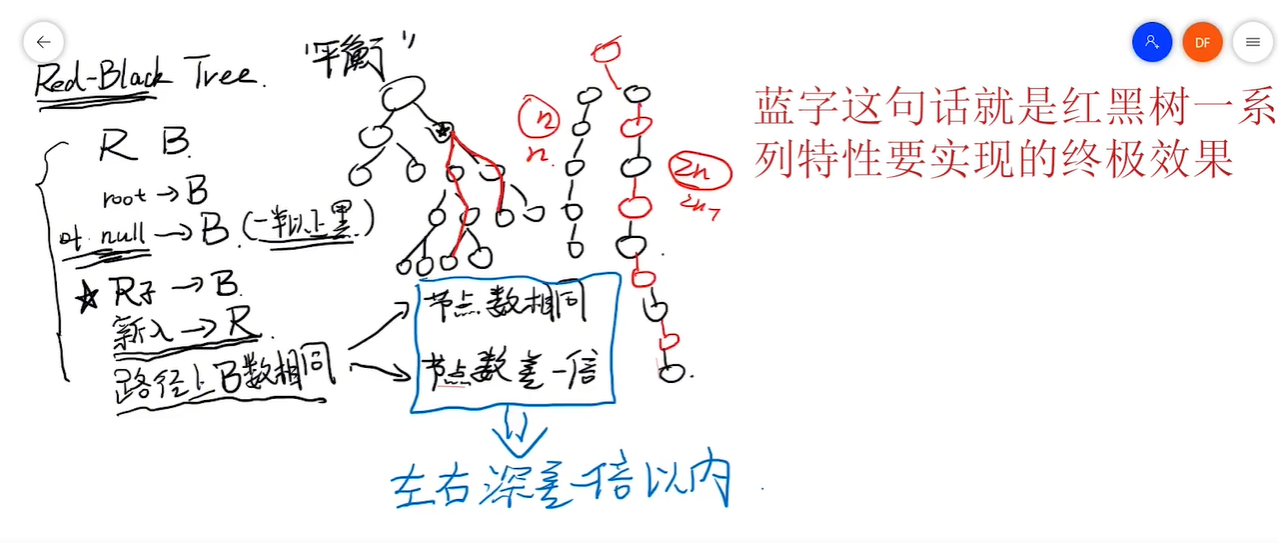
image.png
自平衡二叉树将左右树的深度差限制在1以内,导致的结果是:插入一个数据的时候很容易触发自平衡,自平衡很浪费资源;
红黑树的限定就比自平衡二叉树限定条件宽松很多;插入数据的话,更少的触发自平衡,节省资源;

红黑树调整过程是很有意思的; 将插入的阶段当作红色,然后开始比较其父节点和父节点的兄弟节点(叔节点),然后根据不同的颜色去进行左旋 右旋 并改变颜色;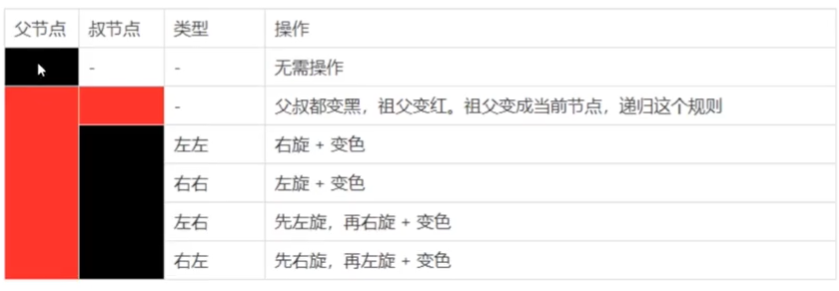image.png
这个过程有个视频讲解:https://www.ixigua.com/6835579764477002247?wid_try=1 这个链接讲的不错;如果不想看视频或者视频丢了,百度一下吧;