本期内容来自B站大佬[https://space.bilibili.com/2030714152]的视频,感谢up主的视频,有兴趣的小伙伴可以去看看https://www.bilibili.com/video/BV1yT4y197gp/?spm_id_from=333.788&vd_source=8ae02c1de2115d30054396cb4aaec183
这里讲到的关于进制的转换可以先看看另一篇
1.6 二进制及位运算
0导读关键字: 二进制 , 小数, float,double,单精度,双精度,IEEE标准
1浮点数的表示
1 先来来看看十进制、二进制整数
十进制的 549 转换成 十进制数的过程其实是:
十进制的 1024 转换成 十进制数的过程其实是:
规律就是从右边第一位开始计数 从左往右看的话:
从右往左看的话:
上述这套过滤如果套入到二进制的话 从左往右看的话:
从右往左看的话:
后续用这样的方式去看 我们有个二进制的1101 转换成十进制数的过程其实是:

很好使哈,二进制的1101就是十进制的13
2 公式拓展到小数
上边说的是整数,下边换成小数,这个还是通用的
公式变成,小数点前的位数从右往左一次是0,1,2,3…n
小数点后的位数从左往右依次是-1,-2,-3,…-n
十进制小数 104.59 就是:
二进制小数 101.11 就是:
实际上这里只是为了套用这样的公式的可行性,确实也可行,但是实际上二进制中没有小数点这个表现形式,公式可行那就是计算机利用存储规则进行落地的事情了;
3 反面教材:
上述整数公式套用在小数上看着好像没有问题,但是吧在一些特殊情况上还是有点瑕疵的
例如 实际上十进制无论如何也表现不出三分之二,只能无限接近,位数越多也就越精确,越接近
;
二进制数据特例跟十进制有异曲同工之妙,例如用上述公式套用转换的话, 换成二进制的表示方式应该是0.001100110011…
上述公式无论如何都是没法真正等于0.2的,只能无限的接近0.2,而且0.001100110011…这个(假)二进制的位数越多结果就是越精准的,但是无限位可能嘛,和明显不合适;这也就是float 喝double 用于小数计算的时候容易失真的缘故!!!
上边基本推导了用二进制去表示小数的可行性,结论是可行的;剩下的就是制定规则规范对这样的进准度问题进行取舍,也是对这套原理真正落地存储指定规则(即:怎么处理点的问题,从哪一位开始时小数点前,哪一位时小数点后),省得每家计算机厂商的规范不一样,导致数据没法正常对接(实际上,远古其实各家厂商对于浮点数的表示规则和运算细节都不一样的,所以程序可移植性基本没有!!)
后来IEEE(eye-triple-e)这套标准、规则统一了所有问题;
4 IEEE标准
1 IEEE基本概念
使用IEEE标准来表示一个浮点数,那么分为三个部分:
- 符号位 s
- 阶码 E
- 尾数 M
float 是32位, 其中 符号位(s) 占1位,阶码(E)占8位,位数(M)占23位;
double是64位, 其中 符号位(s) 占1位,阶码(E)占11位,位数(M)占52位;
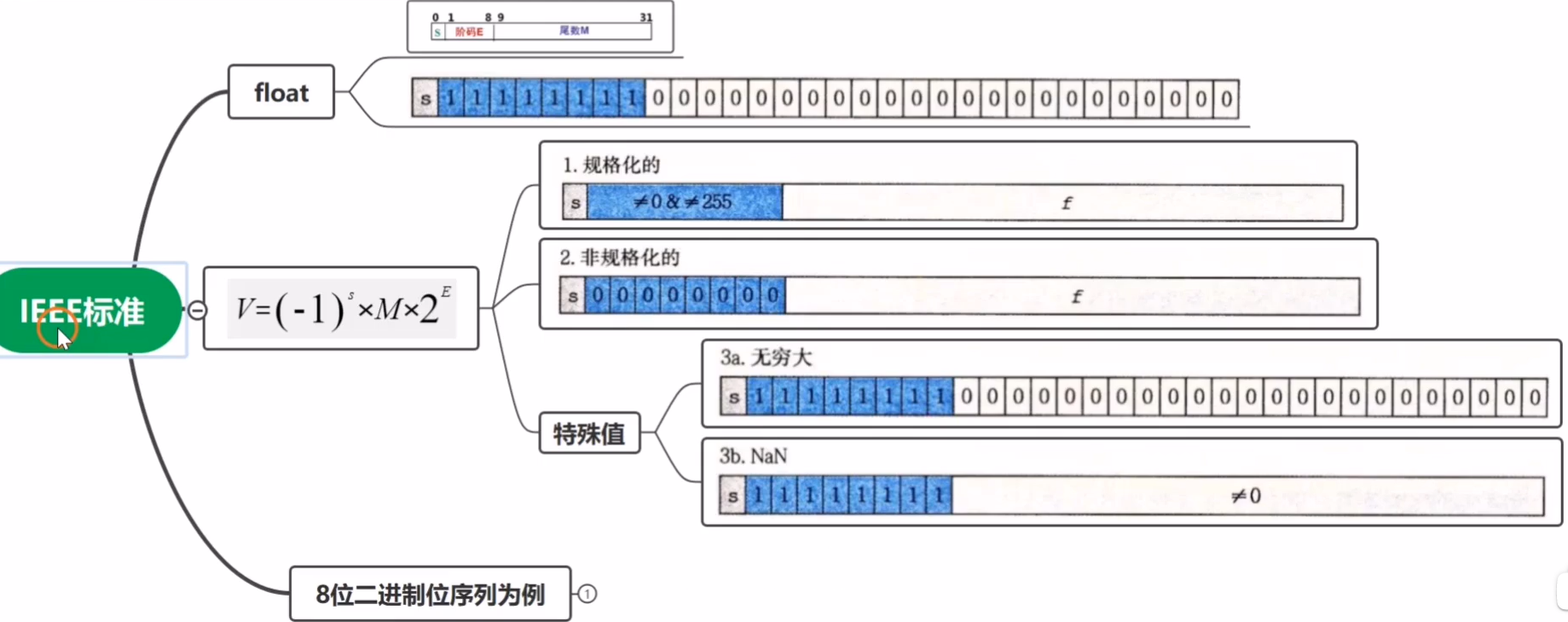
2 IEEE表示公式 (理论 这里讲解是float,单精度)
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
上述公式,最为特殊的就是阶码E了, 一般根据阶码E的值我们可以分为三种不同的情况,
- 规格化的 ( 阶码E八位的值既不是全为1也不是全为0;即:
&&
;全为0全为1的就是特殊值和非规格化了)
- 非规格化的 ( 阶码E的八个比特位都是0
 )
) - 特殊值, 特殊值又非为两种
- 无穷大 (阶码E八位全是1,尾数M全是0
 )
) - NaN (阶码E八位全是1,尾数
 )
)NaN(not a number):不是一个数;
- 无穷大 (阶码E八位全是1,尾数M全是0
5 详细讲解IEEE公式中各部分的计算方式🌟🌟🌟🌟🌟🌟🌟
🌟🌟🌟🌟🌟🌟🌟
下图是更加详细的公式;后分章节我们详细讲解这个公式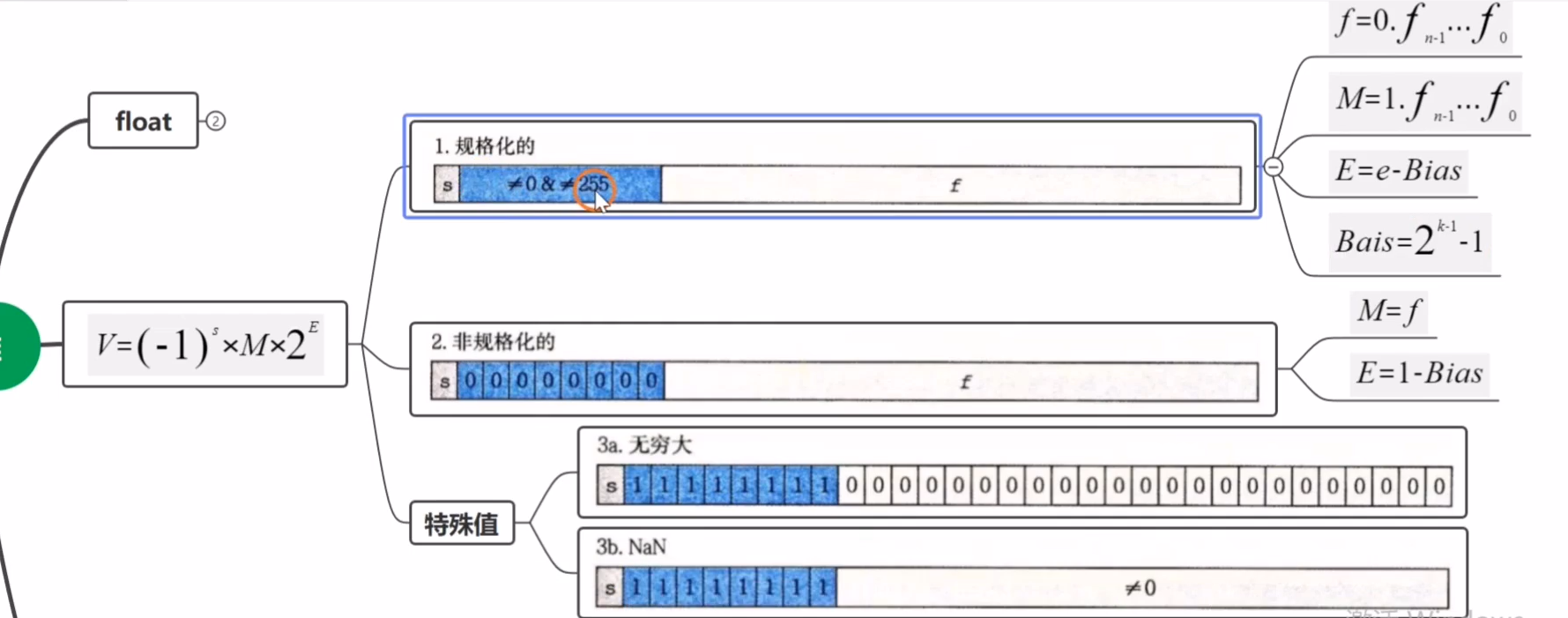
0 参考
我们实际准备一个例子,后续的拆解公式的时候我们详解这个例子;
这里有个二进制数: 0 0000 1011 1101 0000 0000 0000 0000 001
1 符号位S
2 阶码 E
阶码E 是有自己的公式的,并且这个公式还不是简简单单的一个;
首先我们将阶码占有的位置分为类,以float为例子(8位,double11位)
一般根据阶码E的值我们可以分为三种不同的情况,
- 规格化的 ( 阶码E八位的值既不是全为1也不是全为0;即:
&&
;全为0全为1的就是特殊值和非规格化了)
- 非规格化的 ( 阶码E的八个比特位都是0
)
- 特殊值, 特殊值又非为两种
- 无穷大 (阶码E八位全是1,尾数M全是0
)
- NaN (阶码E八位全是1,尾数
)
NaN(not a number):不是一个数;
分为三类之后 ,我们参照[图2-IEEE表公式,可以套用任何类型],就知道了
阶码E在规格化的时候等于
阶码E在非规格化的时候等于
看着两个公式的话, 新印出了一个e;这个东西就是阶码的那8个bit位表示的是一个无符号的数字(0~255),
注意这里说的是那八个bit位标识的是一个无符号的数字,并不是说阶码等于这个数字!这里很重要注意注意注意!!! 阶码的值 是根据这个无符号的值 (规格化 、非规格化),然后跟一个偏移量进行计算得出的;偏移量的大小另外也有一套计算公式;这就导致这个阶码的值并不是简简单单能说清的了,这里就是涉及到不同规则的组合了;下面一点点来(不强制能懂,只要明白,小数足够复杂就行了,)
简单具体点讲:
(阶码部分的8个bit表示的无符号的值 暂时商定为”显示值” 也就是上面公式中的e)
[显示值e]如果是规格化的(八位的值既不是全为1也不是全为0;即:
&&
):这个时候阶码的值等于[显示值e]减去偏移量Bias
,偏移量的计算公式是:
,这里的k表示的是这个阶码部分二进制序列的长度(注意这个阶码的长度并不是一定是8位的,上边说的8位是说的float,单精度的就是8位,double 双精度就是11位了,还能又别的位数,别太死板),我们本篇文章讲的就是float所以这里的k=8;所以偏移量Bias=
;即:阶码值
,e就是阶码部分的8个bit表示的无符号的值 ;
例如例子中的 阶码位置的二进制值是 0000 1011 对应的 阶码计算就是
[显示值e]如果是非规格化的
, float的话,此时
据的例子不是非规格化的,这里先不演示了,后续补充
3 尾数 M
尾数M 跟阶码E一样,也是有自己的公式的,并且也是根据阶码显示值分成三类之后有不同的公式
- 规格化的时候:
又是一个新的概念;他其实就是最最原始的公式计算出来的,用到就是[第二章 公式拓展到小数]的公式;
即:尾数部分就是相当于小数点之后的部分,就可以将小数点之后的部分用的公式进行计算起来了;

例如例子中的 尾数位置的二进制值是 1101 0000 0000 0000 0000 001 对应的 阶码计算就是
- 非规格化的时候
4 总结
所以例子中的结果套用公式就是结果是一个看不懂的数字; 但是公式没有错误,下面我们换一个容易看懂的数字
5 练习
1 练习1 (规格化)
0 1000 0011 1101 0000 0000 0000 0000 0002 练习2(规格化)
0 1000 0011 1101 0000 1000 0000 0000 0003 练习3(非规格化)
0 0000 0000 1000 0000 0000 0000 0000 000
上述结果用代码验证一下是对的上的;
@Testpublic void test(){System.out.println(Long.toBinaryString(Float.floatToIntBits(29.0f)));System.out.println(Long.toBinaryString(Float.floatToIntBits(29.03125f)));/*结果:0 1000 0011 1101 0000 0000 0000 0000 0000 1000 0011 1101 0000 1000 0000 0000 000*/int intBits = Integer.parseInt("00000000010000000000000000000000", 2);System.out.println(intBits); // 6832128float f = Float.intBitsToFloat(intBits); // 这个方法就是将 二进制字符串00000000010000000000000000000000转换成float 不过这里只接受实际值的intbits作为参数,所以经过了Integer.parseInt(str,radix)的转换System.out.println(f); // 5.877472E-39 //这个位置很好的诠释了单精度的有效位数就是7/*Integer.parseInt(String s, int radix)就是将整数字符串s(radix用来指明s是几进制)转换成10进制的整数,显然前提是s为整数字符串。比如 s可以为“1314520”、“5201314”等。不可以为“我爱你一生一世”或者“I love you forever”等之类的非整数字符串。那么,Integer.pareseInt("10086",10)就是将10进制整数字符串“10086”转换成10进制的整数10086。Integer.parseInt("00000000010000000000000000000000", 2); 就是将 二进制的00000000010000000000000000000000转换成十进制表示的 intbits(6832128)*/}
至此,浮点数表现形式我已经讲解完毕了,下边是对浮点数的计算了
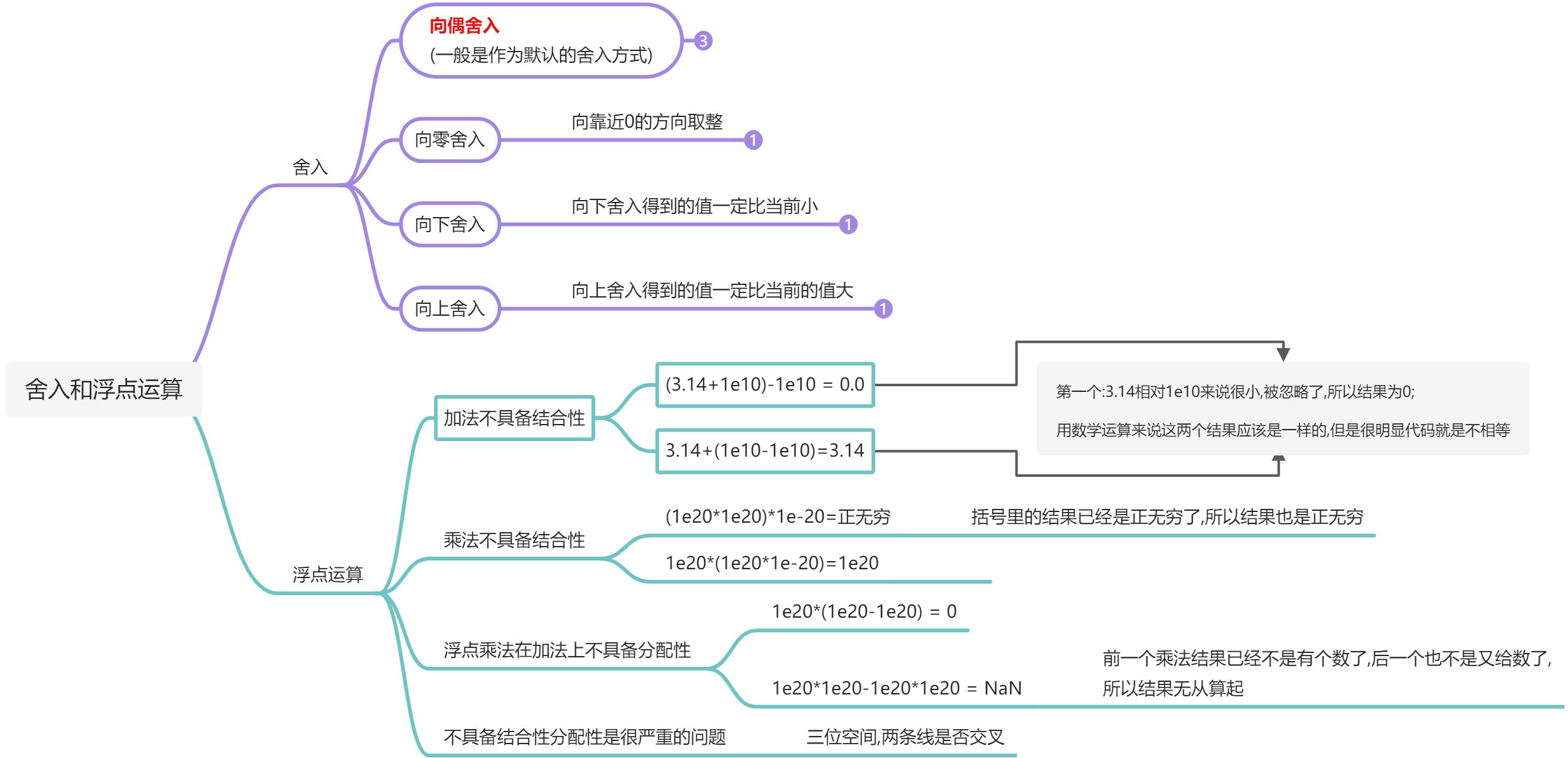
2 舍入和浮点数的运算
3单精度双精度比区别
1解释1
- 单精度和双精度的字节数不同。前者占4个字节(32位);后者占8个字节(64位)。
单精度和双精度有效数字位数不同。前者为8位;后者为16位。 ()
从该数的第一个非零数字起,直到末尾数字止的数字称为有效数字
如:
(1)0.618的有效数字有三个,分别是6,1,8
(2)5.2*10^6,只有5和2是有效数字
(3)1100.120 有7位有效数字。单精度和双精度表示的数的范围不同。前者的数值范围在-3.40E+38 到 +3.40E+38之间;后者的范围为-1.79E+308到+1.79E+308之间。
-
2解释2:(我更喜欢这个)
1.单精度浮点型(float):
专指占用32位存储空间的单精度(single-precision)值。单精度在一些处理器上比双精度更快而且只占用双精度一半的空间,但是当值很大或者很小的时候,他将变得不精确,当你需要小数部分并且对精度的要求不高时,单精度浮点型的变量是有用的。
2.双精度型:
正如它的关键词“double”,占用64位的存储空间。在一些现代的被优化用来进行高速数学计算的处理器上双精度型实际比单精度的快。所有超出人类经验的数学函数,如sin,cos和sqrt均返回双精度的值。当你需要保持多次反复迭代的计算的精确性时,或在操作值很大的数字时,双精度型时做好的选择。
单精度/双精度实际上存储的是一个近似值,浮点的特性决定了他可以存储非常小的数,也可以存储极大的数,它的数据精确度并不是一个绝对值,而是存储值得百分比,所以即使对同一组数据定义也是不可以将float型和double型数据比较的。3 解释3
c语言中的单精度浮点数的实际有效精度为24位二进制,这相当于 24log102≈7.2 位10进制的精度。尾数用23位存储,加上默认的小数点前的1位1,2^(23+1) = 16777216。因为 10^7 < 16777216 < 10^8,所以说单精度浮点数的有效位数是7位。
扩展资料:单精度浮点数是用来表示带有小数部分的实数,一般用于科学计算。在计算机存储器中占用4个位元(32 bits)存储空间,包括符号位1位,阶码8位,尾数23位。利用“浮点”(浮动小数点)的方法,可以表示一个范围很大的数值。其数值范围为-3.4E38~3.4E38。*单精度浮点数最多有7位十进制有效数字,如果某个数的有效数字位数超过7位,当把它定义为单精度变量时,超出的部分会自动四舍五入。单精度浮点数的指数用“E”或“e”表示。00000000010000000000000000000000 这个二进制串,如果按照IEEE标准计算的话,得到的值实际上应该是5.8774717541114375398436826861112e-39 但是同样的串用代码去转换的话,得到的确实7位有效数字; int intBits = Integer.parseInt("00000000010000000000000000000000", 2); System.out.println(intBits); // 6832128 float f = Float.intBitsToFloat(intBits); System.out.println(f); // 5.877472E-39 //这个位置很好的诠释了单精度的有效位数就是7
解释二最精简, 解释1+解释三最科学!