排序算法介绍

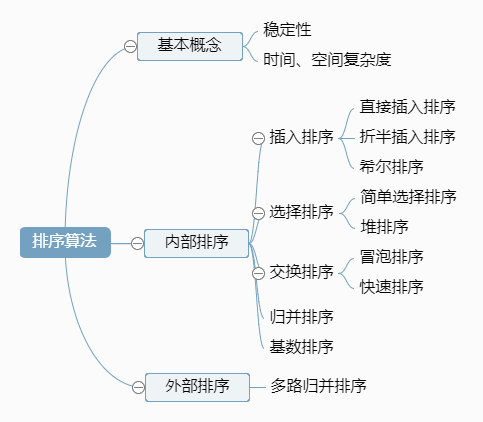
数据结构基本排序算法 Java 实现 - 图1

1. 基本概念

  • 稳定性： 待排序的数列中，若两个元素的值相等 R1 = R2 ，在排序结束之后，元素之间的相对位置没有发生变化，则称排序算法是稳定的，否则是不稳定的。算法是否具有稳定性并不能衡量一个算法的优劣，它主要是对算法性质进行描述。

2. 内部排序

排序期间元素全部存放在内存中。

2.1 插入排序

每次将待排序的元素插入到前面已排好序的子序列中

2.1.1 直接插入排序

  • 思路： 第 i 次排序，将第 i 个元素插入到前面 i - 1 个已排序好的子序列中

  • 时间复杂度

    • 最好情况：表中元素已经有序，每插入一个元素，都只需要比较一次而不需要移动元素，时间复杂度为 O（n）
    • 最坏情况：表中元素顺序与结果中想要的顺序相反，那么比较次数就是 2+3+…+ n 次的和，时间复杂度为 O（n^2）
    • 平均情况：最好情况和最坏情况的平均值 O（n^2）

  • 空间复杂度： 仅使用了常数个辅助单元，空间复杂度为 O（1）

  • 稳定性： 每次待插入的元素都是从后面往前面先比较后移动，若找到相同元素，相同位置也不会发生变化，即是稳定的排序算法

  • 适用场景：元素有序，元素较少

  • 代码实现：

    1. public void fun3(int[] array){
    2.   if (array == null || array.length == 0){
    3.       return;
    4.   }
    5.   for (int i = 1; i < array.length ; i++) {
    6.       int temp = array[i];
    7.       int k = i-1;
    8.       while (k >= 0 && temp < array[k]){
    9.           array[k+1] = array[k];
    10.           k--;
    11.       }
    12.       array[k+1] = temp;
    13.   }
    14. }

2.1.2 折半插入排序

  • 思路： 与直接插入排序类似，只是查找元素待插入位置 k 的时候，使用的是折半查找

  • 时间复杂度

    • 只是减少了比较元素的次数，约为O（nlogn），但元素的移动次数仍然依赖于序列的原始状态，故时间复杂度情况与直接插入排序相同

  • 空间复杂度： 仅使用了常数个辅助单元，空间复杂度为 O（1）

  • 代码实现：

    1. public void fun(int[] array){
    2.   if (array == null || array.length == 0){
    3.       return;
    4.   }
    5.   for (int i = 1; i < array.length; i++) {
    6.       int temp = array[i];
    7.       int low = 0;
    8.       int high = i-1;
    9.       while (low <= high){
    10.           int mid = (low + high) / 2;
    11.           if (temp < array[mid]){
    12.               high = mid - 1;
    13.           } else {
    14.               low = mid + 1;
    15.           }
    16.       }
    17.       for (int j = i; j > low; j--) {
    18.           array[j] = array[j-1];
    19.       }
    20.       array[low] = temp;
    21.   }
    22. }

2.1.3 希尔排序

  • 思路： 又称 缩小增量排序，将原序列分割为多个L [ i，i + d，i + 2d，+…+ i + kd ] 的子序列，满足这个间隔 d 的元素分配在同一个子序列，并进行直接插入排序，并缩小 d 值，待 d 值为 1 时，在进行最后一次直接插入排序，d 值初始值为 n / 2

  • 时间复杂度

    • 据说是数学难题，不好分析，最坏情况为O（n^2）

  • 空间复杂度： 仅使用了常数个辅助单元，空间复杂度为 O（1）

  • 稳定性： 相同元素可能被划分到不同子序列，相对位置可能发生变化，故为不稳定的排序算法

  • 代码实现： 三层 for 循环 or 二层 for 循环

  1. public void fun2(int[] array){
  2.     if (array == null || array.length == 0){
  3.         return;
  4.     }
  5.     for (int gap = array.length / 2;gap > 0;gap /= 2) {
  6.         for (int i = gap; i <  array.length; i++) {
  7.             int temp = array[i];
  8.             int k = i-gap;
  9.             while (k >= 0 && temp < array[k]){
  10.                 array[k+gap] = array[k];
  11.                 k -= gap;
  12.             }
  13.             array[k+gap] = temp;
  14.         }
  15.     }
  16. }

2.2 选择排序

在第 i 趟排序中，从后面的 n - i + 1 个待排序的元素中选取最小的元素作为第 i 个元素，直到第 n - 1 趟排序走完，只剩 1 个待排序的元素。注意，插入排序是将待排序的元素插入到前面已排序的序列中，选择排序是将后面子序列中选取最小（大）值放到最终位置

2.2.1 简单选择排序

  • 思路： 原序列为L [1… n] ，在第 i 次排序中，从 子序列 L [i .. n] 中选取最小值与 L [i] 进行交换

  • 时间复杂度

    • 具体查看代码实现方式，O（n^2）

  • 空间复杂度： 仅使用了常数个辅助单元，空间复杂度为 O（1）

  • 稳定性： 不稳定，例如 5 8 5 2 9，第一次排序后，第一个 5 和 2 交换了位置。

  • 代码实现：

    1. public void fun(int[] array){
    2.   if (array == null || array.length <= 1){
    3.       return;
    4.   }
    5.   for (int i = 0; i < array.length; i++) {
    6.       int index = i;
    7.       for (int j = i+1; j <  array.length; j++) {
    8.           if (array[j] < array[index]){
    9.               index = j;
    10.           }
    11.       }
    12.       if (index != i){
    13.           int temp = array[index];
    14.           array[index] = array[i];
    15.           array[i] = temp;
    16.       }
    17.   }
    18. }

2.2.2 堆排序：这个比较复杂，后续再更新

  • 思路： 将原序列按照层次遍历的方式构成完全二叉树，然后构建大根堆，大根堆满足父节点的值大于等于子节点的值，输入根节点的值，然后再进行堆调整。若节点 i 为中间节点，则父节点索引为 (i – 1) / 2，左右子结点索引分别为 2 i + 1 和 2 i + 2 。

  • 时间复杂度

    • 构建大根堆时间为O（n），之后有n-1次调整操作，每次调整时间复杂度为O（h），故最好、最坏、平均情况下时间复杂度为O（nlogn）

  • 空间复杂度： 仅使用了常数个辅助单元，空间复杂度为 O（1）

  • 稳定性：

  • 代码实现：

2.3 交换排序

比较两个元素的关键值大小来交换它们的位置

2.3.1 冒泡排序

  • 思路： 序列从索引 0 开始，元素之间两两比较，若为逆序则进行交换，最终能得到最大的值，然后再从左到右，进行比较交换，得到第二大的值，上一轮得到的数字不必进行比较，此排序每次能得到一个最小（大）值。

  • 时间复杂度

    • 最好情况：序列已经满足有序，无需交换，复杂度为O（n）
    • 最坏情况：序列逆序，为O（n^2）
    • 平均情况：O（n^2）

  • 空间复杂度： 仅使用了常数个辅助单元，空间复杂度为 O（1）

  • 稳定性： 若算法中，i > j 且 L[i] = L[j] 不交换，则算法是稳定的，依算法具体规则定

  • 代码实现：

    1. public void fun (int[] array){
    2.   for (int i = 0; i < array.length; i++) {
    3.       for (int j = 0; j < array.length - i - 1; j++) {
    4.           if (array[j] > array[j+1]){
    5.               int temp = array[j];
    6.               array[j] = array[j+1];
    7.               array[j+1] = temp;
    8.           }
    9.       }
    10.   }
    11. }

2.3.2 快速排序

  • 思路： 基于分治思想，在原序列 L 中选择任意一个元素作为基准，经过一趟排序之后将原序列分为两个部分 L [1…k-1] 和 L [k+1…n]，其中 L [1…k-1] 内的元素值小于等于基准值，L [k+1…n] 内的元素值大于等于基准值，然后递归地对上述两个子序列进行上述操作，知道子序列中只含有一个元素值即可。

  • 时间复杂度

    • 最好情况：序列已经满足有序，无需交换，复杂度为O（n）
    • 最坏情况：序列逆序，为O（n^2）
    • 平均情况：O（n^2）

  • 空间复杂度： 仅使用了常数个辅助单元，空间复杂度为 O（1）

  • 稳定性： 若算法中，i > j 且 L[i] = L[j] 不交换，则算法是稳定的，依算法具体规则定

  • 代码实现：

  1. public void fun(int[] array,int low,int high){
  2.     if (high <= low){
  3.         return;
  4.     }
  5.     int i = low;
  6.     int j = high;
  7.     int temp = array[i];
  8.     while(i < j){
  9.         // 注意后面判断条件，不能都只 > temp，否则遇到 array[i] == array[j] 时会进入死循环。
  10.         while(i<j && array[j] >= temp){
  11.             j--;
  12.         }
  13.         if (i < j){
  14.             array[i] = array[j];
  15.         }
  16.         while(i<j && array[i] < temp){
  17.             i++;
  18.         }
  19.         if (i < j){
  20.             array[j] = array[i];
  21.         }
  22.     }
  23.     array[i] = temp;
  24.     fun(array,low,i-1);
  25.     fun(array,i+1,high);
  26. }
  27. void fun1(int[] array,int low,int high){
  28.     if (low > high){
  29.         return;
  30.     }
  31.     int key = array[low];
  32.     int i = low;
  33.     int j = high;
  34.     while (i < j){
  35.         while (i < j && array[j] >= key){
  36.             j--;
  37.         }
  38.         while (i<j && array[i] <= key){
  39.             i++;
  40.         }
  41.         if (i < j){
  42.             int temp = array[i];
  43.             array[i] = array[j];
  44.             array[j] = temp;
  45.         }
  46.     }
  47.     array[low] = array[i];
  48.     array[i] = key;
  49.     fun1(array,low,i-1);
  50.     fun1(array,i+1,high);
  51. }

2.4 归并排序

  • 思路： 假设待排序表含有 n 个记录，则可以看做是 n 个有序的子表，每个子表长度为 1 ，然后两两合并，得到 n / 2 个长度为 1 或 2 的有序表；再两两合并，直到合并成一个长度为 n 的有序表，这种排序方法称为 2-路归并排序

  • 时间复杂度

    • 平均情况：每一趟归并的时间复杂度为O（n），共进行 logn 趟归并，故算法的时间复杂度为 O（nlogn）

  • 空间复杂度： 合并的过程中，辅助空间要占用 n 个单元，故时间复杂度为 O（n）

  • 稳定性： 由于合并操作不会改变相同关键字记录的相对次序，所以2-路归并算法是稳定的排序方法

  • 代码实现：

  1. public void (int[] array,int low,int high){
  2.     if (low >= high){
  3.         return;
  4.     }
  5.     int mid = low + (high - low) / 2;
  6.     fun(array,low,mid);
  7.     fun(array,mid+1,high);
  8.     merge(array,low,mid,high);
  9. }
  11. public void merge(int[] array,int low,int mid,int high){
  12.     int temp = new int[high-low+1];
  13.     int i = low;
  14.     int j = mid+1;
  15.     int k = 0;
  16.     while (i <= mid && j<= high ){
  17.         if (array[i] < array[j]){
  18.             temp[k++] = array[i++];
  19.         }else{
  20.             temp[k++] = array[j++];
  21.         }
  22.     }
  23.     while(i<=mid){
  24.         temp[k++] = array[i++];
  25.     }
  26.     while(j <= high){
  27.         temp[k++] = array[j++];
  28.     }
  29.     for(int l =0;l<temp.length;l++){
  30.         array[low+l] = temp[l];
  31.     }
  32. }

2.5 基数排序

  • 思路：基数排序是一种很特殊的排序方法，他不是基于比较进行排序的，而是采用多关键字排序的思想，借助分配和收集两种操作对单逻辑关键字进行排序。基数排序又分为最高位优先（MSD）和最低位优先（LSD）排序

  • 时间复杂度：O (nlog(r)m)，其中 r 为所采取的基数，而 m 为堆数

  • 空间复杂度：

  • 稳定性：稳定的

  • 代码实现：基数排序