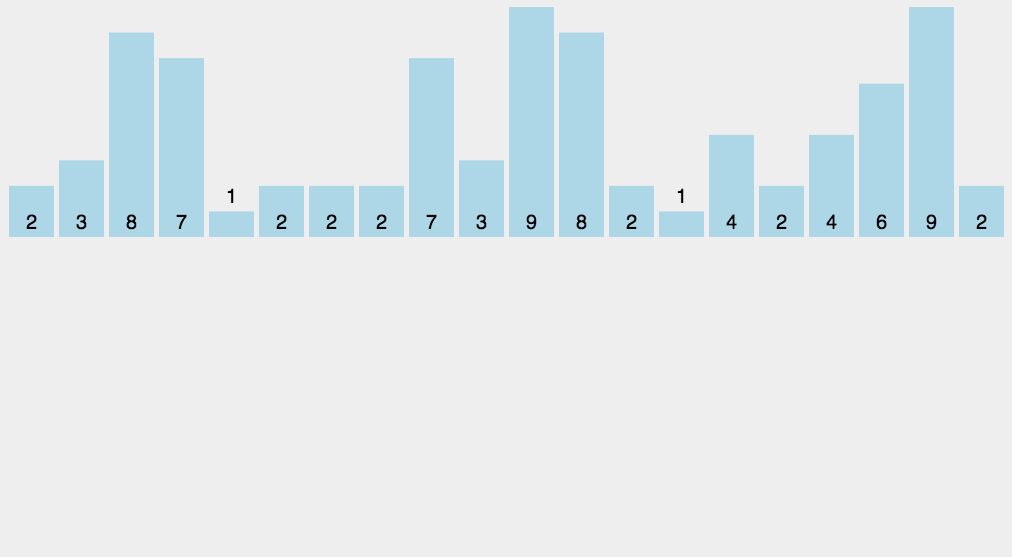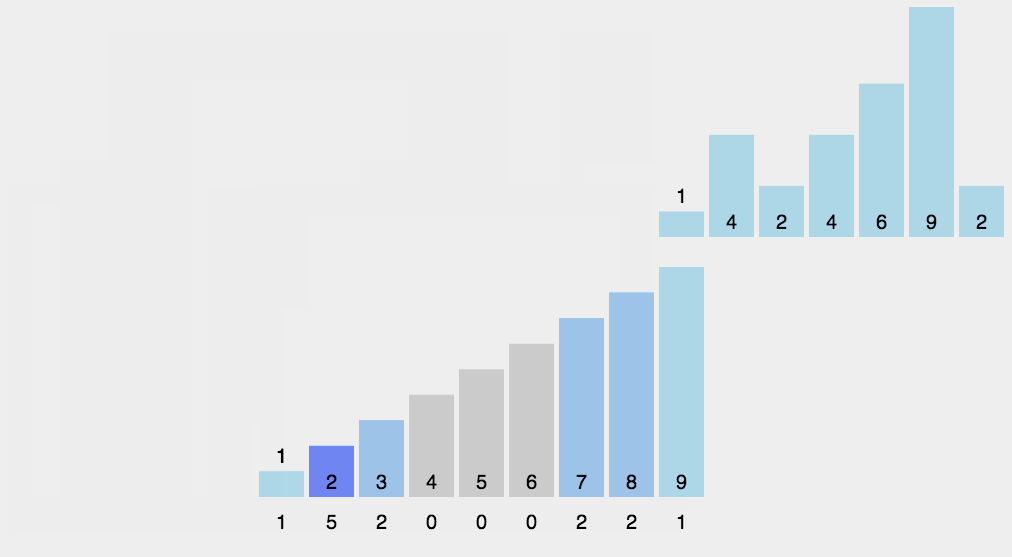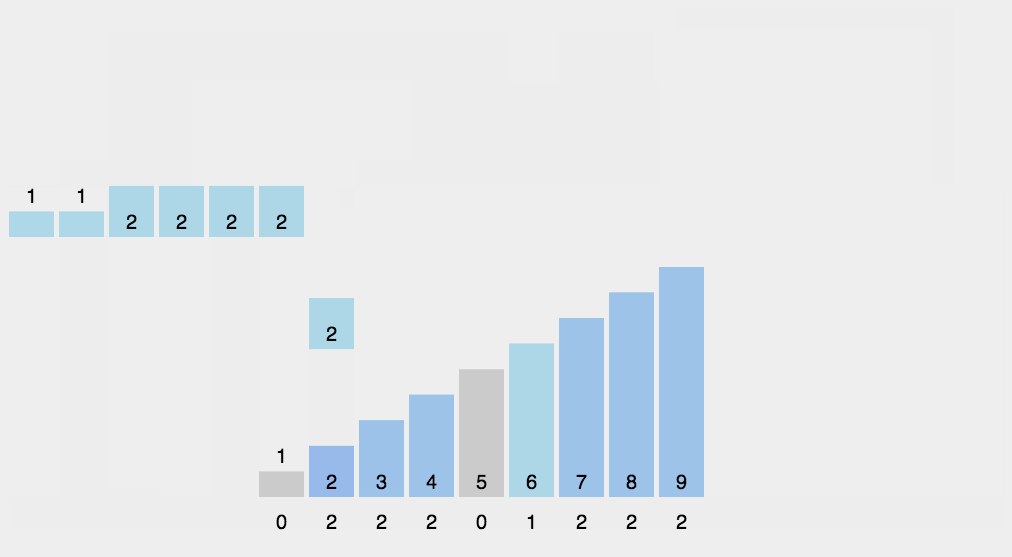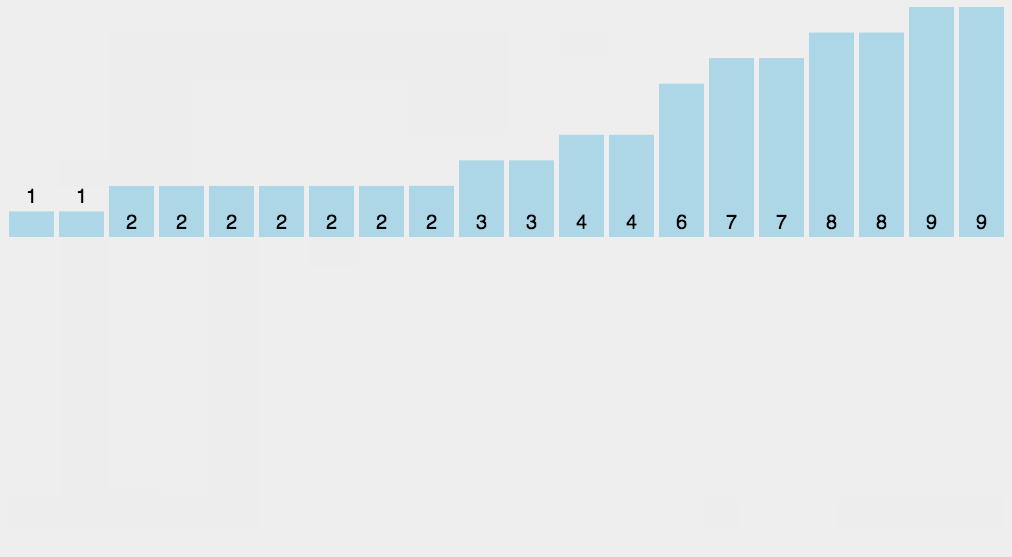计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

8.1 算法描述

  • 找出待排序的数组中最大和最小的元素；
  • 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
  • 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；

  • 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

    8.2 动图演示

    8、计数排序（Counting Sort） - 图1

    8.3 代码实现

    1. function countingSort(arr, maxValue) {
    2.   varbucket =newArray(maxValue + 1),
    3.       sortedIndex = 0;
    4.       arrLen = arr.length,
    5.       bucketLen = maxValue + 1;
    7.   for(vari = 0; i < arrLen; i++) {
    8.       if(!bucket[arr[i]]) {
    9.           bucket[arr[i]] = 0;
    10.       }
    11.       bucket[arr[i]]++;
    12.   }
    14.   for(varj = 0; j < bucketLen; j++) {
    15.       while(bucket[j] > 0) {
    16.           arr[sortedIndex++] = j;
    17.           bucket[j]--;
    18.       }
    19.   }
    21.   returnarr;
    22. }

    8.4 算法分析

    计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时，时间复杂度是O(n+k)，空间复杂度也是O(n+k)，其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。