何谓递归？程序反复调用自身即是递归。此处禁止套娃！
以下会举例说明我对递归的一点理解，如果你不想看下去了，请记住这几个问题怎么回答：

  1. 如何给一堆数字排序？ 答：分成两半，先排左半边再排右半边，最后合并就行了，至于怎么排左边和右边，请重新阅读这句话。
  2. 孙悟空身上有多少根毛？ 答：一根毛加剩下的毛。
  3. 你今年几岁？ 答：去年的岁数加一岁，1999 年我出生。

递归代码最重要的两个特征：结束条件和自我调用。自我调用是在解决子问题，而结束条件定义了最简子问题的答案。

解题三部曲

  1. 找整个递归的终止条件：递归应该在什么时候结束？
  2. 找返回值：应该给上一级返回什么信息？
  3. 本级递归应该做什么：在这一级递归中，应该完成什么任务？

二叉树的最大深度

  1. 找终止条件。什么情况下递归结束？当然是树为空的时候，此时树的深度为0，递归就结束了。
  2. 找返回值。应该返回什么？题目求的是树的最大深度，我们需要从每一级得到的信息自然是当前这一级对应的树的最大深度，因此我们的返回值应该是当前树的最大深度，这一步可以结合第三步来看。
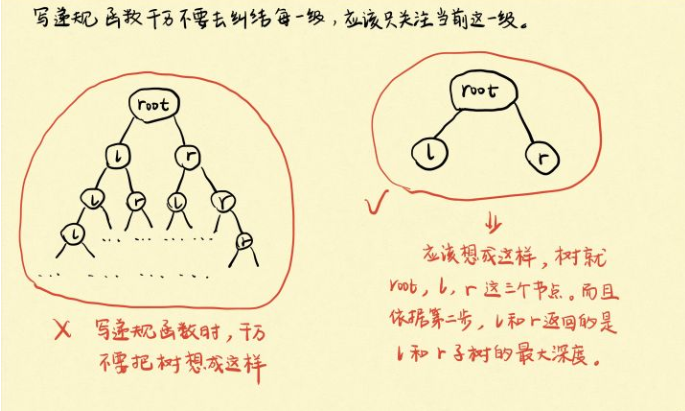
  3. 本级递归应该做什么。首先，还是强调要走出之前的思维误区，递归后我们眼里的树一定是这个样子的，看下图。此时就三个节点：root、left、right，其中根据第二步，left和right分别记录的是root的左右子树的最大深度。那么本级递归应该做什么就很明确了，自然就是在root的左右子树中选择较大的一个，再加上1就是以root为根的子树的最大深度了，然后再返回这个深度即可。

image.png

深度优先(DFS)

对于一颗二叉树，深度优先搜索(Depth First Search)是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。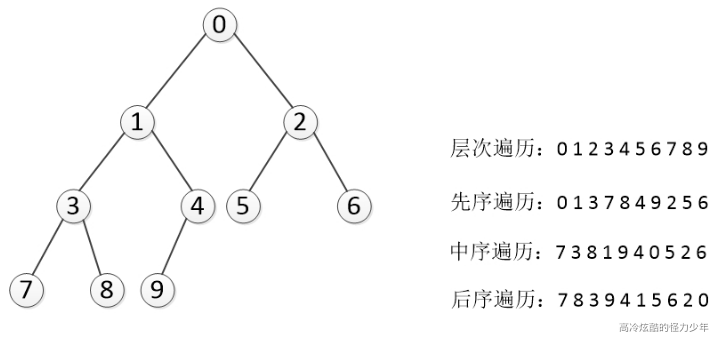
二叉树 - 图2

先序遍历（根左右）

  1. class Solution(object):
  2.     def preorderTraversal(self, root):
  3.         方法一：递归
  4.         res = []
  5.         def dfs(root):
  6.             if root == None:
  7.                 return
  8.             res.append(root.val)
  9.             dfs(root.left)
  10.             dfs(root.right)
  11.         dfs(root)
  12.         return res
  15.         方法二：循环+栈迭代实现
  16.         if not root:
  17.             return
  18.         stack = []
  19.         node = root
  20.         res = []
  21.         while stack or node:
  22.             while node:
  23.                 # 先保存当前值
  24.                 res.append(node.val)
  25.                 # 把左边所有都压入栈
  26.                 stack.append(node)
  27.                 node = node.left
  28.             # 然后再把右边所有都压入栈
  29.             node = stack.pop()
  30.             node = node.right
  31.         return res

中序遍历（左根右）

  1. class Solution(object):
  2.     def inorderTraversal(self, root):
  3.         方法一：递归
  4.         res = []
  5.         def dfs(root):
  6.             if not root:
  7.                 return
  8.             dfs(root.left)
  9.             res.append(root.val)
  10.             dfs(root.right)
  11.         dfs(root)
  12.         return res
  14.         方法二：循环+栈迭代实现
  15.         if not root:
  16.             return 
  18.         stack = []
  19.         node = root
  20.         res = []
  21.         while stack or node:
  22.             # 先把左边所有都压入栈
  23.             while node:
  24.                 stack.append(node)
  25.                 node = node.left
  26.             # 将栈里的节点的值保存到res
  27.             node = stack.pop()
  28.             res.append(node.val)
  29.             # 然后再把右边所有都压入栈
  30.             node = node.right
  31.         return res

后序遍历（左右根）

  1. class Solution(object):
  2.     def postorderTraversal(self, root):
  3.         方法一：递归
  4.         res = []
  5.         def dfs(root):
  6.             if not root:
  7.                 return
  8.             dfs(root.left)
  9.             dfs(root.right)
  10.             res.append(root.val)
  11.         dfs(root)
  12.         return res
  14.         方法二：循环+栈迭代
  15.         if not root:
  16.             return 
  18.         stack = [] 
  19.         node = root
  20.         res = []
  21.         while stack or node:
  22.             while node: # 下行循环，直到找到第一个叶子节点
  23.                 stack.append(node)
  24.                 if node.left: # 能左就左，不能左就右
  25.                     node = node.left 
  26.                 else:
  27.                     node = node.right     
  28.             node = stack.pop()
  29.             res.append(node.val)
  30.             # 如果当前节点是上一节点的左子节点，则遍历右子节点
  31.             if stack and node == stack[-1].left: 
  32.                 node = stack[-1].right
  33.             else:
  34.                 node = None
  35.         return res
  37.         方法三：投机取巧法，使用逆先序遍历
  38.         if not root:
  39.             return []
  41.         stack = []
  42.         node = root
  43.         res = []
  44.         while stack or node:
  45.             while node:
  46.                 res.append(node.val)
  47.                 stack.append(node)
  48.                 node = node.right # 此处和下面的left相反
  49.             node = stack.pop()
  50.             node = node.left
  51.         return res[::-1]

广度优先(BFS)

从树的root开始，从上到下从从左到右遍历整个树的节点

  1. class Solution:
  2.     def levelOrder(self, root: TreeNode) -> List[int]:
  3.         # 利用队列实现树的层次遍历
  4.         if not root:
  5.             return
  7.         res = []
  8.         queue = [root]
  9.         while queue:
  10.             node = queue.pop(0)
  11.             res.append(node.val)
  13.             if node.left:
  14.                 queue.append(node.left)
  15.             if node.right:
  16.                 queue.append(node.right)
  17.         return res

二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）
示例：二叉树：[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层序遍历结果：
[
[3],
[9,20],
[15,7]
]

  1. class Solution(object):
  2.     def levelOrder(self, root):
  3.         # 利用队列实现树的层次遍历
  4.         if not root:
  5.             return []
  7.         res = []
  8.         queue = [root]
  9.         while queue:
  10.             # 因为题目要求用子列表表示，这里是和广度优先遍历唯一区别
  11.             level = []
  12.             for _ in range(len(queue)):
  13.                 node = queue.pop(0)
  14.                 level.append(node.val)
  15.                 # 如果左子节点存在，入队列
  16.                 if node.left:
  17.                     queue.append(node.left)
  18.                 # 如果右子节点存在，入队列
  19.                 if node.right:
  20.                     queue.append(node.right)
  21.             res.append(level)  # 如果是从下向上遍历，这需要把这里改成头插 res.insert(0, level)
  22.         return res

二叉树的最小深度

  1. class Solution:
  2.     # 方法一：递归
  3.     # 可以通过递归求左右节点的最小深度的较小值，也可以层序遍历找到第一个叶子节点所在的层数。
  4.     def minDepth(self, root: TreeNode) -> int:
  5.         if not root:
  6.             return
  8.         if not root.left and not root.right:
  9.             return 1 
  10.         if not root.right:
  11.             return 1 + self.minDepth(root.left)
  12.         if not root.left:
  13.             return 1 + self.minDepth(root.right)
  14.         return 1 + min(self.minDepth(root.left), self.minDepth(root.right))  
  16.         # 方法二：BFS利用队列实现树的层次遍历
  17.         if not root:
  18.             return 0
  20.         depth = 1
  21.         queue = [root]
  22.         while queue:
  23.             for i in range(len(queue)):
  24.                 node = queue.pop(0) # 切记要先取出
  25.                 if not node.left and not node.right:
  26.                     return depth
  27.                 if node.left:
  28.                     queue.append(node.left)
  29.                 if node.right:
  30.                     queue.append(node.right)
  31.             depth += 1
  32.         return depth

二叉树的最大深度

基本思路就是递归，当前树的最大深度等于（1+max(左子树最大深度，右子树最大深度)）

  1. class Solution:
  2.     def maxDepth(self, root):
  3.         # 方法一：dfs递归
  4.         if not root:
  5.             return 0
  6.         return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
  8.         # 方法二：BFS利用队列实现树的层次遍历
  9.         if not root:
  10.             return 0
  12.         queue = [root]
  13.         depth = 0
  14.         while queue:
  15.             for i in range(len(queue)):
  16.                 node = queue.pop(0)
  17.                 if node.left:
  18.                     queue.append(node.left)
  19.                 if node.right:
  20.                     queue.append(node.right)
  21.             depth += 1
  22.         return depth

验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。根节点的值为 5 ，但是其右子节点值为 4 。

  1. class Solution(object):
  2.     def isValidBST(self, root):
  3.         # 方法一：中序遍历
  4.         stack = []
  5.         inorder = float('-inf')
  7.         while stack or root:
  8.             while root:
  9.                 stack.append(root)
  10.                 root = root.left
  11.             root = stack.pop()
  12.             # 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
  13.             if root.val <= inorder:
  14.                 return False
  15.             inorder = root.val
  16.             root = root.right
  17.         return True
  19.         # 方法二：递归，根据左<中<右的特点判断
  20.         def dfs(root, left, right):
  21.             if not root:
  22.                 return True
  23.             elif left < root.val < right:
  24.                 return dfs(root.left, left, root.val) and dfs(root.right, root.val, right)
  25.             else:
  26.                 return False
  27.         return dfs(root,float('-inf'), float('inf'))

二叉树镜像

  1. class Solution:
  2.     def Mirror(self, root):
  3.         if not root:
  4.             return
  6.         #互换左右孩子的值
  7.         root.right, root.left = root.left, root.right
  8.         #递归处理左子树
  9.         self.Mirror(root.right)
  10.         #递归处理右子树
  11.         self.Mirror(root.left)
  12.         return root

对称二叉树

给定一个二叉树，检查它是否是镜像对称的。
例如，二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3

  1. class Solution(object):
  2.     def isSymmetric(self, root):
  3.         # 方法一：递归算法  
  4.         if not root:
  5.             return True
  6.         def dfs(left, right):
  7.             # 递归的终止条件是两个节点都为空
  8.             # 或者两个节点中有一个为空
  9.             # 或者两个节点的值不相等
  10.             if not left and not right:
  11.                 return True
  12.             if not left or not right:
  13.                 return False
  14.             if left.val != right.val:
  15.                 return False 
  16.             ret1 = dfs(left.left, right.right)
  17.             ret2 = dfs(left.right, right.left)
  18.             return ret1 and ret2
  19.         # 用递归函数，比较左节点，右节点
  20.         return dfs(root.left, root.right)
  22.         # 方法二：迭代算法
  23.         if not root:
  24.             return True
  25.         deq = deque([root.left, root.right])
  26.         while deq:
  27.             root_right = deq.pop()
  28.             root_left = deq.pop()
  29.             if root_left == None and root_right == None:
  30.                 continue
  31.             if root_left == None or root_right == None:
  32.                 return False
  33.             if root_left.val != root_right.val:
  34.                 return False
  35.             deq.extend([root_left.left, root_right.right, root_left.right, root_right.left])
  36.         return True

二叉树中和为某一值的路径

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例:
给定如下二叉树，以及目标和 sum = 22，
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]

  1. class Solution(object):
  2.     def pathSum(self, root, target):
  3.         # 栈+递归方法
  4.         lists = []
  5.         stack = []
  6.         def dfs(root, nums):
  7.             if not root:
  8.                 return
  10.             stack.append(root.val)
  11.             nums -= root.val
  12.             if nums == 0 and not root.left and not root.right:
  13.                 lists.append(list(stack))
  15.             dfs(root.left, nums)
  16.             dfs(root.right, nums)
  17.             stack.pop()
  19.         dfs(root, target)
  20.         return lists

二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。
注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]

  1. class Solution(object):
  2.     def insertIntoBST(self, root, val):
  3.         if not root:
  4.             return TreeNode(val) 
  5.         node = root
  6.         # 思路不难，比较node.val和val，小并且左边没孩子就放左边，大并且右边没孩子就放右边
  7.         while node:
  8.             if val < node.val:
  9.                 if not node.left:
  10.                     node.left = TreeNode(val)
  11.                     break
  12.                 else:
  13.                     node = node.left
  14.             else:
  15.                 if not node.right:
  16.                     node.right = TreeNode(val)
  17.                     break
  18.                 else:
  19.                     node = node.right
  20.         return root

删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。
root = [5,3,6,2,4,null,7]
key = 3
5
/ \
3 6
/ \ \
2 4 7
给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7]

  1. # 找到后有四种情况
  2. # case0 结点不存在，empty,return root
  3. # case1 结点没孩子,直接删除
  4. # case2 结点只有一个孩子,是左孩子,让左孩子即位
  5. # case3 结点只有一个孩子,是右孩子,让右孩子即位
  6. # case4 结点有俩孩子,用 right tree left most 替换待删除结点,然后把right tree left most那个结点删除
  7. class Solution:
  8.     def deleteNode(self, root, key):
  9.         # 方法一：慢慢找一层一层遍历
  10.         if root is None:
  11.             return root
  13.         if root.val > key:
  14.             root.left = self.deleteNode(root.left, key)
  15.         elif root.val < key:
  16.             root.right = self.deleteNode(root.right, key)
  17.         else:
  18.             # case1 没有孩子,直接删除返回空
  19.             if not root.left and not root.right:
  20.                 root = None
  21.                 return root
  22.             # case2 只有一个孩子,左孩子,让左孩子即位
  23.             elif root.left and not root.right:
  24.                 tmp = root.left
  25.                 root = None
  26.                 return tmp
  27.             # case3 只有一个孩子,右孩子,让右孩子即位
  28.             elif not root.left and root.right:
  29.                 tmp = root.right
  30.                 root = None
  31.                 return tmp
  32.             # case4 有两个孩子,和右子树 left most交换后在右子树中删除 left most
  33.             else:
  34.                 curr = root.right # 右子树
  35.                 while curr.left: # find left most
  36.                     curr = curr.left
  37.                 # 退出while循环时候的curr就是left most
  38.                 root.val = curr.val # 即位
  39.                 root.right = self.deleteNode(root.right, curr.val) # 在右子树中删除该结点后作为新的右子树
  40.         return root
  42.         # 方法二：递归
  43.         def dfs(root, key, l):
  44.             if not root:
  45.                 return l
  46.             if root.val == key:
  47.                 return dfs(root.right, key, root.left)
  48.             elif root.val < key:
  49.                 root.right = dfs(root.right, key, l)
  50.                 return root
  51.             else:
  52.                 root.left = dfs(root.left, key, l)
  53.                 return root
  55.         return dfs(root, key, None)

树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构， 即 A中有出现和B相同的结构和节点值。
给定的树 A:
3
/ \
4 5
/ \
1 2
给定的树 B：
4
/
1
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。
输入：A = [1,2,3], B = [3,1]
输出：false
输入：A = [3,4,5,1,2], B = [4,1]
输出：true

  1. class Solution(object):
  2.     def isSubStructure(self, A, B):
  3.         if not A or not B:
  4.             return False
  6.         def dfs(A, B):
  7.             if not B:
  8.                 return True
  9.             if not A:
  10.                 return False
  11.             if A.val != B.val:
  12.                 return False
  13.             return dfs(A.left, B.left) and dfs(A.right, B.right)
  14.         return dfs(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B)

按之字形顺序打印二叉树

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

  1. class Solution(object):
  2.     def zigzagLevelOrder(self, root):
  3.         # 方法一：按照广度优先的模版套就行了，区别就是正向插入和反向插入
  4.         if not root:
  5.             return []
  7.         # index记录层数奇偶
  8.         index = 1
  9.         res = []
  10.         queue = [root]
  11.         while queue:
  12.             # 获取queue的长度，因为队列的长度是在不断变化的，这里需先确定要遍历多少次
  13.             level = []
  14.             for _ in range(len(queue)):
  15.                 node = queue.pop(0)
  16.                 level.append(node.val)
  17.                 if node.left:
  18.                     queue.append(node.left)
  19.                 if node.right:
  20.                     queue.append(node.right)
  22.             # 当index为奇数时，就正向输出
  23.             if index & 1 == 1:
  24.                 res.append(level)
  25.             # 当index偶位数时，就反向输出，即先调用一次reverse，再保存
  26.             else:
  27.                 res.append(level[::-1])
  28.             index += 1
  29.         return res
  32.         # 方法二：使用递归
  33.         if not root:
  34.             return []
  35.         # index记录层数奇偶
  36.         index = 0
  37.         res = []
  39.         def dfs(root, index):
  40.             if not root:
  41.                 return
  42.             if len(res) == index:
  43.                 res.append([])
  44.             # 当index为偶数时，就直接头插
  45.             if index & 1 == 0:
  46.                 res[index].append(root.val)
  47.             # 当index为奇数时，就直接尾插
  48.             else:
  49.                 res[index].insert(0, root.val)
  50.             dfs(root.left, index + 1)
  51.             dfs(root.right, index + 1)
  52.         dfs(root, index)
  53.         return res

二叉搜索树中第K小的元素

给定一棵二叉搜索树，请找出其中的第k小的结点。例如，（5，3，7，2，4，6，8）中，按结点数值大小顺序第三小结点的值为4。

  1. class Solution:
  2.     def kthSmallest(self, root, k):
  3.         # 方法一：DFS中序遍历递归法，然后根据切片取值
  4.         res = []
  5.         def dfs(root):
  6.             if not root:
  7.                 return
  8.             dfs(root.left) # 如果求第K大的元素，和下面的right互换即可
  9.             res.append(root.val)
  10.             dfs(root.right)
  11.         dfs(root)
  12.         return res[k-1] 
  15.         # 方法二：DFS中序遍历循环压栈法
  16.         stack = []
  17.         node = root
  18.         while True:
  19.             # 先把左边所有都压入栈
  20.             while node:
  21.                 stack.append(node)
  22.                 node = root.left
  23.             node = stack.pop()
  24.             # 唯一区别就是这里计数了
  25.             k -= 1
  26.             if k == 0:
  27.                 return node.val
  29.             node = node.right

二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”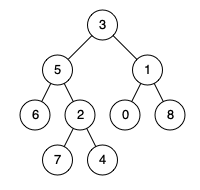
二叉树 - 图3
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

  1. class Solution(object):
  2.     def lowestCommonAncestor(self, root, p, q):
  3.         if not root:
  4.             return None
  5.         # 边界条件，如果匹配到left或right就直接返回停止递归
  6.         if root.val == p.val or root.val == q.val:
  7.             return root
  9.         # 因为是DFS算法，这个模板可以无脑套用，写上之后可能你思路就清晰很多
  10.         left = self.lowestCommonAncestor(root.left, p, q)
  11.         right = self.lowestCommonAncestor(root.right, p, q)
  12.         # 如果左子树找不到，那就在右子树，如果右子树找不到，那就在左子树
  13.         if not left: 
  14.             return right
  15.         if not right: 
  16.             return left
  17.         return root

寻找重复的子树

给定一棵二叉树，返回所有重复的子树。对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。
两棵树重复是指它们具有相同的结构以及相同的结点值。
1
/ \
2 3
/ / \
4 2 4
/
4
下面是两个重复的子树：
2
/
4
和
4

  1. class Solution(object):
  2.     def findDuplicateSubtrees(self, root):
  3.         # 递归
  4.         # “重复”也就是说既需要知道以当前节点为根的子树什么样，也需要知道以其他节点为根的子树长啥样
  5.         dicts = {}
  6.         res = []
  8.         def dfs(root):
  9.             if not root:
  10.                 return '#'
  11.             tmp = dfs(root.left) + ',' + dfs(root.right) + ',' + str(root.val)
  12.             if tmp in dicts:
  13.                 dicts[tmp] += 1
  14.             else:
  15.                 dicts[tmp] = 1
  16.             if dicts[tmp] == 2:
  17.                 res.append(root)
  18.             return tmp
  20.         dfs(root)
  21.         return res

二叉搜索树转换为双向链表*

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。
为了让您更好地理解问题，以下面的二叉搜索树为例：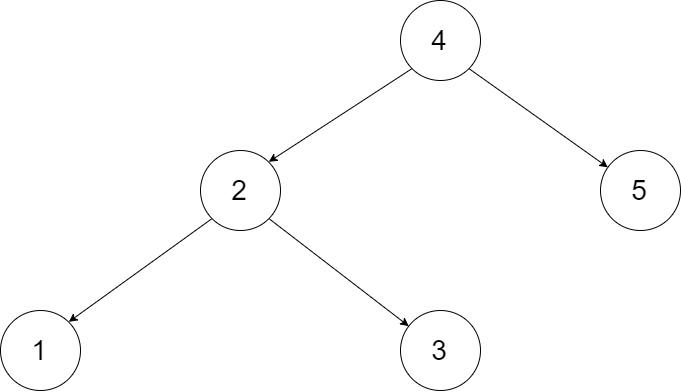
二叉树 - 图4
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。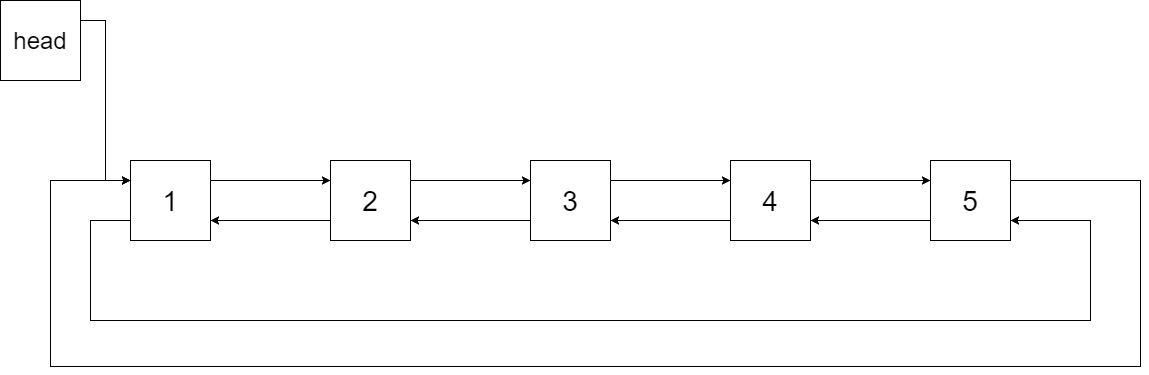
二叉树 - 图5
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

  1. class Solution(object):
  2.     def treeToDoublyList(self, root):
  3.         # 1.这里定义全局的head和pre。
  4.         # 2.整体思路按照中序遍历来走，pre如果为空则表示是这棵树左下的节点，那么将其定义为头节点。
  5.         # 3.如果pre不空的话，就表示当前遍历的节点的左子树的右下节点。
  6.         # 4.遍历完成后，pre指向这棵树右下的节点。
  7.         # 5.最后将其首尾连接起来。
  8.         if not root: 
  9.             return
  11.         def dfs(cur):
  12.             if not cur: 
  13.                 return
  14.             dfs(cur.left) # 递归左子树
  15.             if self.pre: # 修改节点引用
  16.                 self.pre.right, cur.left = cur, self.pre
  17.             else: # 记录头节点
  18.                 self.head = cur
  19.             self.pre = cur # 保存 cur
  20.             dfs(cur.right) # 递归右子树
  22.         self.pre = None
  23.         dfs(root)
  24.         self.head.left, self.pre.right = self.pre, self.head
  25.         return self.head

从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。
注意:你可以假设树中没有重复的元素。
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：
3
/ \
9 20
/ \
15 7

  1. Solution(object):
  2.     def buildTree(self, preorder, inorder):      
  3.         if len(inorder) == 0:
  4.             return None
  5.         # 创建一棵新树
  6.         root = TreeNode(preorder[0])
  7.         # 在中序中找到前序第一个节点的位置，中序遍历中mid的左边全是左子树，右边全是右子树
  8.         mid = inorder.index(preorder[0])
  10.         # 构建左子树
  11.         root.left = self.buildTree(preorder[1:mid+1], inorder[:mid])
  12.         # 构建右子树
  13.         root.right = self.buildTree(preorder[mid+1:], inorder[mid+1:])
  14.         return root