时间复杂度
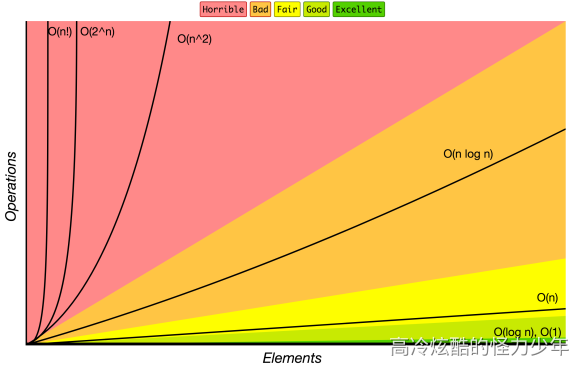
| 大O标记法 | 计算10个元素 | 计算100个元素 | 计算1000个元素 |
|---|---|---|---|
| O(1) | 1 | 1 | 1 |
| O(log N) | 3 | 6 | 9 |
| O(N) | 10 | 100 | 1000 |
| O(N log N) | 30 | 600 | 9000 |
| O(N^2) | 100 | 10000 | 1000000 |
| O(2^N) | 1024 | 1.26e+29 | 1.07e+301 |
| O(N!) | 3628800 | 9.3e+157 | 4.02e+2567 |
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
空间复杂度
顺序表(数组)
数组元素在内存中存放是连续的,每个元素占用的内存相同。数组可以通过下标迅速访问数组中的任何元素O(1)。但是在数组中增加一个元素时,需要移动大量元素,在内存中空出一个元素的空间,然后将要增加的元素放进其中O(n)。同理,要删除一个元素,需要移动大量元素来填掉被移动的元素O(n)。
如果需要快速访问数据,很少插入和删除元素,使用数组。
链表
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是不像数组一样连续存储数据,而是在每一个节点(数据存储单元)里存放下一个节点的位置信息(内存地址)。
数组和链表的区别
- 存储位置:数组将元素在内存中连续存放,而链表中的元素在内存中不是顺序存储的。
- 存储空间:一般情况下,存储相同多的数据,数组占用的内存较少,而链表还需要存储前驱和后继,需要更多的内存。
- 长度的可变性:数组的长度在定义的时候给定,如果存储的数据个数超过数组的初始长度,会发生溢出,而链表的长度可以按实际情况伸缩。
- 按序号查找:按序号查找时,数组可以随机访问,时间复杂度为O(1),而链表不支持随机访问,平均时间复杂度为O(n)。
- 按值查找:如果数组是无序的,数组和链表的时间复杂度均为O(n),如果数组是有序的,使用二分查找可以使时间复杂度降低到O(logn)。
- 插入和删除:数组平均需要移动n/2个元素,而链表只需要修改指针。
哈希表可以结合数组和链表的优点
| 数组 | 链表 | |
|---|---|---|
| 读取 | O(1) | O(n) |
| 插入 | O(n) | O(1) |
| 删除 | O(n) | O(1) |
链表有三种类型(单向链表、单向循环链表、双面链表)
class SingleNode:"""单链表的结点"""def __init__(self,item):# item存放数据元素self.item = item# next是下一个节点的标识self.next = Noneclass SingleLinkList:"""单链表"""def __init__(self):self._head = Nonedef is_empty(self):"""判断链表是否为空"""return self._head == Nonedef length(self):"""链表长度"""# cur初始时指向头节点cur = self._headcount = 0# 当到达尾部时,尾节点指向Nonewhile cur != None:count += 1# 将cur后移一个节点cur = cur.nextreturn countdef travel(self):"""遍历链表"""cur = self._headwhile cur != None:print(cur.item, end=" ")cur = cur.nextdef add(self, item):"""头部添加元素"""# 先创建一个保存item值的空节点node = SingleNode(item)# 将新节点的链接域next指向头节点,即_head指向的位置node.next = self._head# 将链表的头_head指向新节点self._head = nodedef append(self, item):"""尾部添加元素"""node = SingleNode(item)# 先判断链表是否为空,若是空链表,则将_head指向新节点if self.is_empty():self._head = node# 若不为空,则找到尾部,将尾节点的next指向新节点else:cur = self._headwhile cur.next != None:cur = cur.nextcur.next = nodedef insert(self, pos, item):"""指定位置添加元素"""# 若指定位置pos为第一个元素之前,则执行头部插入if pos <= 0:self.add(item)# 若指定位置超过链表尾部,则执行尾部插入elif pos > (self.length()-1):self.append(item)# 找到指定位置else:node = SingleNode(item)count = 0# pre用来指向指定位置pos的前一个位置pos-1,初始从头节点开始移动到指定位置pre = self._headwhile count < (pos-1):count += 1pre = pre.next# 先将新节点node的next指向插入位置的节点node.next = pre.next# 将插入位置的前一个节点的next指向新节点pre.next = nodedef remove(self,item):"""删除节点"""cur = self._headpre = Nonewhile cur != None:# 找到了指定元素if cur.item == item:# 如果第一个就是删除的节点if cur == self._head:# 将头指针指向头节点的后一个节点self._head = cur.nextelse:# 将删除位置前一个节点的next指向删除位置的后一个节点pre.next = cur.nextbreakelse:# 继续按链表后移节点pre = curcur = cur.nextdef search(self,item):"""链表查找节点是否存在,并返回True或者False"""cur = self._headwhile cur != None:if cur.item == item:return Truecur = cur.nextreturn False# 测试代码if __name__ == "__main__":ll = SingleLinkList()ll.add(1)ll.add(2)ll.append(3)ll.insert(2, 4)print("length:",ll.length())ll.travel()print(ll.search(3))print(ll.search(5))ll.remove(1)print("length:",ll.length())ll.travel()
双向链表
一种更复杂的链表是“双向链表”或“双面链表”。每个节点有两个链接:一个指向前一个节点,当此节点为第一个节点时,指向空值;而另一个指向下一个节点,当此节点为最后一个节点时,指向空值。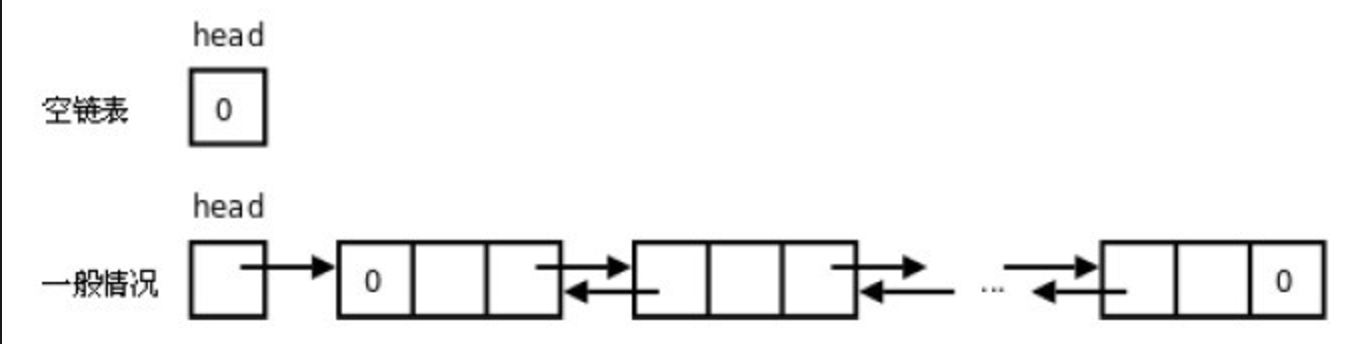
链表中的元素在内存中不是顺序存储的,它们通过元素中的指针联系起来。每个元素包括两个部分,一个是存储的数据,一个是指向下一个元素的指针。
如果需要访问链表中的一个元素,需要从第一个元素开始,一直找到需要的元素位置。
但是增加和删除一个元素就非常简单,只需要改变元素中的指针。
如果经常需要插入和删除元素,使用链表。
栈(先入后出)
栈(stack),有些地方称为堆栈,是一种容器,可存入数据元素、访问元素、删除元素,它的特点在于只能允许在容器的一端(称为栈顶端指标,英语:top)进行加入数据(英语:push)和输出数据(英语:pop)的运算。没有了位置概念,保证任何时候可以访问、删除的元素都是此前最后存入的那个元素,确定了一种默认的访问顺序。
由于栈数据结构只允许在一端进行操作,因而按照后进先出(LIFO, Last In First Out)的原理运作。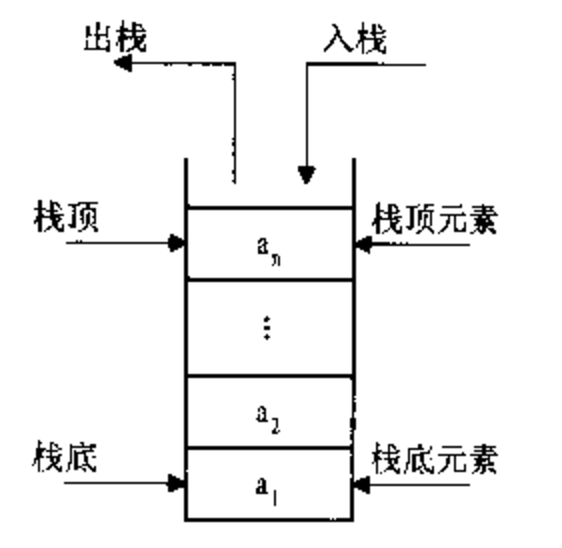
class Stack(object):"""栈"""def __init__(self):self.items = []def is_empty(self):"""判断是否为空"""return self.items == []def push(self, item):"""加入元素"""self.items.append(item)def pop(self):"""弹出元素"""return self.items.pop()def peek(self):"""返回栈顶元素"""return self.items[len(self.items)-1]def size(self):"""返回栈的大小"""return len(self.items)if __name__ == "__main__":stack = Stack()stack.push("hello")stack.push("world")stack.push("itcast")print(stack.size())print(stack.peek())print(stack.pop())print(stack.pop())print(stack.pop())
队列(先入先出)
队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列是一种先进先出的(First In First Out)的线性表,简称FIFO。允许插入的一端为队尾,允许删除的一端为队头。队列不允许在中间部位进行操作!假设队列是q=(a1,a2,……,an),那么a1就是队头元素,而an是队尾元素。这样我们就可以删除时,总是从a1开始,而插入时,总是在队列最后。这也比较符合我们通常生活中的习惯,排在第一个的优先出列,最后来的当然排在队伍最后。
有两种类型(单端队列、双端队列)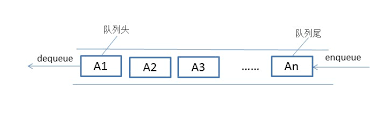

双端队列
双端队列(deque,全名double-ended queue),是一种具有队列和栈的性质的数据结构。
双端队列中的元素可以从两端弹出,其限定插入和删除操作在表的两端进行。双端队列可以在队列任意一端入队和出队。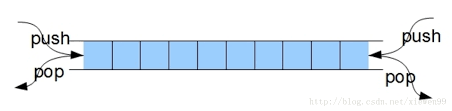
堆
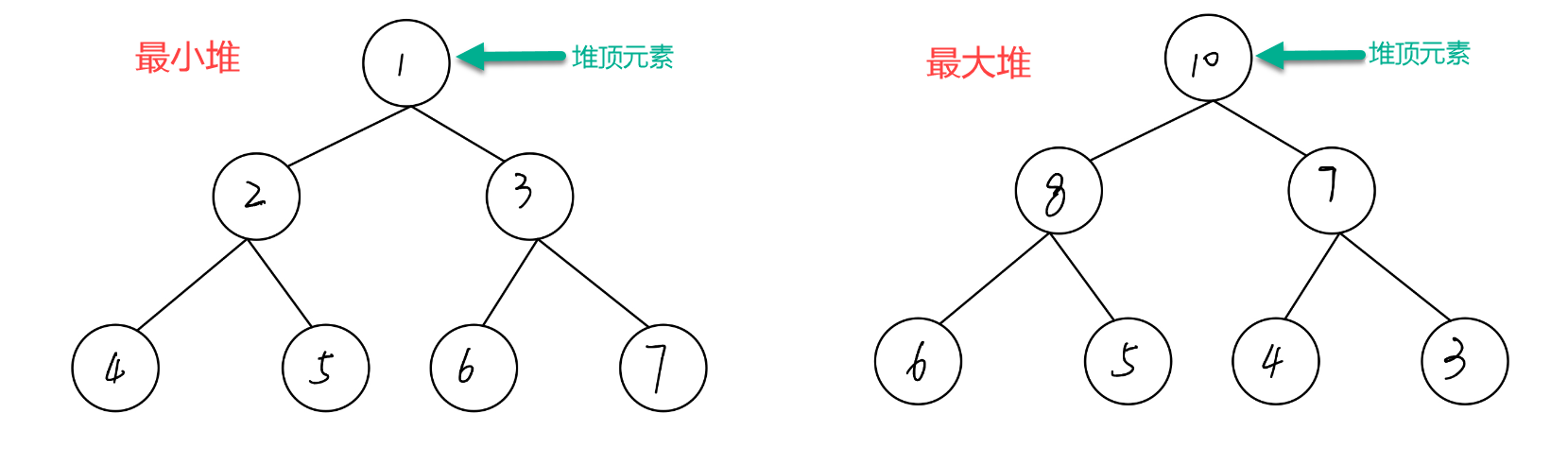
堆是一种特别的二叉树,满足以下条件的二叉树,可以称之为 堆
- 完全二叉树
- 每一个节点的值都必须 大于等于或者小于等于 其孩子节点的值
特点:
- 可以在 O(logN) 的时间复杂度内向 堆 中插入元素
- 可以在 O(logN) 的时间复杂度内向 堆 中删除元素
- 可以在 O(1) 的时间复杂度内获取 堆 中的最大值或最小值
堆的分类
- 最大堆:堆中每一个节点的值 都大于等于 其孩子节点的值。所以最大堆的特性是 堆顶元素(根节点)是堆中的最大值
- 最小堆:堆中每一个节点的值 都小于等于 其孩子节点的值。所以最小堆的特性是 堆顶元素(根节点)是堆中的最小值
import heapqnums = [2, 43, 45, 23, 12]# 创建堆,会生成一个从小到大排列的数组,Py默认都是最小堆,如果想用最大堆,可以自己加负号heapq.heapify(nums)[2, 12, 23, 45, 43]# 弹出堆顶元素,也就是头部print(heapq.heappop(nums))2# 加入堆heapq.heappush(nums, 3)# 查询最大的1个值,这个数字可以自定义,此操作不会弹出元素print(heapq.nlargest(1, nums))[45]# 查询最小的1个值,这个数字可以自定义,此操作不会弹出元素print(heapq.nsmallest(1, nums))[3]# 弹出所有值print([heapq.heappop(nums) for _ in range(len(nums))])[2, 12, 23, 43, 45]
TopK堆解法
class Solution(object):def findKthLargest(self, nums, k):# 这里使用了自建堆,可以使用[0]等索引方法heap = [x for x in nums[:k]]heapq.heapify(heap)for i in range(k, len(nums)):if nums[i] > heap[0]:heapq.heappop(heap)heapq.heappush(heap, nums[i])return heap[0]# 另一种方法,常用heap = []for i in nums:heapq.heappush(heap, i)if len(heap) > k:heapq.heappop(heap)return heap[0]
建堆的时间复杂度
建堆的方式有两种,比较常见的建堆方式是自底向上,因为时间复杂度更低,为O(N)
- 自顶向下的建堆方式,这个方式是从根节点开始,然后一个个的插入堆的末尾,向上进行调整。该建堆方式的时间复杂度为 O(logN)
- 自底向上的建堆方式,这个方式是从倒数第二层的节点(叶子节点的上一层)开始,从右向左,从下到上的向下进行调整。 O(N)

