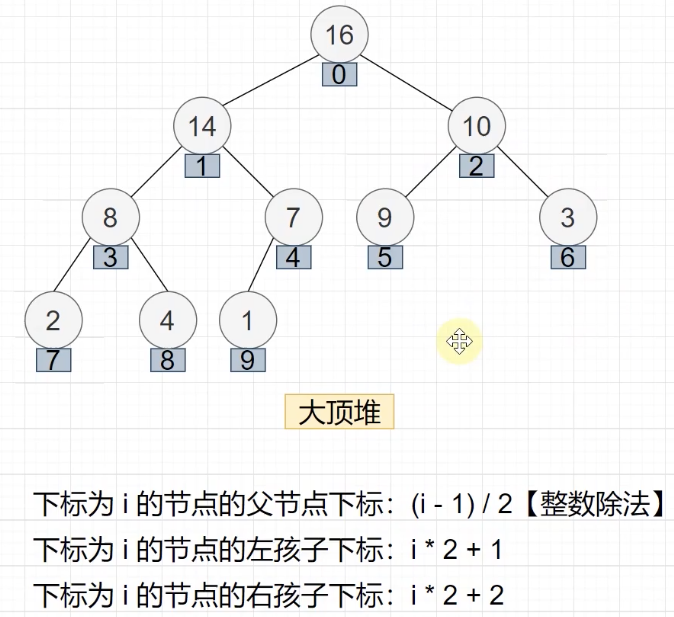
堆

逻辑结构是完全二叉树
分为大顶堆(大根堆)和小顶堆(小根堆)

大顶堆每一个父节点要大于左右子节点
image.png

堆排序

想要一个从大到小的序列 ,就需要构造一个大顶堆,取根节点,再把剩下的元素构造成大顶堆
一个完整的堆排序需要经过反复的两个步骤:
构造堆结构和堆排序输出

  1. public class HeapSort {
  2.     public static void main(String[] args) {
  3.         int[] arr = {6, 8, 7, 9, 5, 4, 3, 2, 1};
  4.         sort(arr);
  5.         System.out.println(Arrays.toString(arr));
  6.     }
  8.     private static void sort(int[] arr) {
  10.         //1.构建大顶堆
  11.         for (int i = arr.length / 2 - 1; i >= 0; i--) {
  12.             //从第一个非叶子结点从下至上，从右至左调整结构
  13.             adjustBigHeap(arr, i, arr.length);
  14.         }
  15.         //2.调整堆结构+交换堆顶元素与末尾元素
  16.         for (int j = arr.length - 1; j > 0; j--) {
  17.             //将堆顶元素与末尾元素进行交换
  18.             swap(arr, 0, j);
  19.             //重新对堆进行调整
  20.             adjustBigHeap(arr, 0, j);
  21.         }
  22.     }
  24.     /**
  25.      * 构建大顶堆
  26.      *
  27.      * @param arr    数组
  28.      * @param i      非叶子节点位置
  29.      * @param length 需要调节的数组长度(主键减少)
  30.      */
  31.     private static void adjustBigHeap(int[] arr, int i, int length) {
  32.         // 保存当前需要调整的节点值
  33.         int temp = arr[i];
  35.         // k: 非叶子节点的左子节点  处理 左子节点k 和
  36.         for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
  37.             //如果左子结点小于右子结点，k指向右子结点
  38.             if (k + 1 < length && arr[k] < arr[k + 1]) {
  39.                 k++;
  40.             }
  41.             //如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
  42.             if (arr[k] > temp) {
  43.                 arr[i] = arr[k];
  44.                 i = k;
  45.             } else {
  46.                 break;
  47.             }
  48.         }
  50.         //将temp值放到最终的位置
  51.         arr[i] = temp;
  52.     }
  54.     /**
  55.      * 交换元素
  56.      *
  57.      * @param arr
  58.      * @param a
  59.      * @param b
  60.      */
  61.     public static void swap(int[] arr, int a, int b) {
  62.         int temp = arr[a];
  63.         arr[a] = arr[b];
  64.         arr[b] = temp;
  65.     }
  66. }

作用

找第K大(小)元素

静态数据集合
针对静态数据集合，我们可以通过数据集合建立大小为k的堆，若是大顶堆，则堆顶元素为第 k 小元素，否则为第 k 大元素。
动态数据集合
针对动态数据集合，我们可以一直维护一个大小为k的堆，增加元素时，将元素与堆顶元素比较，若为大顶堆，并且比对顶元素小，则替换，再堆化，得到新的第 k 小元素。
具体案例与代码：LeetCode：703. Kth Largest Element in a Stream

优先队列

队列：先进先出，后进后出。
优先队列：优先级高的先出队。
堆可以直接看做一个优先队列，入队，即往堆中添加元素，并且按照优先级堆化，而出队时，即堆顶元素为优先级最高的元素。
Java 中的 PriorityQueue 是优先级队列的一种实现。

求动态集合中位数

一组具有n个元素的有序数据中，若元素个数为偶数，则 n2\frac{n}{2}2n 和 n2+1\frac{n}{2}+12n+1 位置的元素取一个作为中位数，若元素个数为偶数，则中位数在 n2+1\frac{n}{2}+12n+1 位置。
堆排序 - 图2