判断回溯很简单，拿到一个问题，你感觉如果不穷举一下就没法知道答案，那就可以开始回溯了。

模版

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

解决一个回溯问题，实际上就是一个决策树的遍历过程。只需要思考3个问题：

  1. 路径：也就是已经做出的选择。
  2. 选择列表：也就是你当前可以做的选择。
  3. 结束条件：也就是到达决策树底层，无法再做选择的条件。

回溯算法的框架

  1. res = []
  2. def dfs(路径, 选择列表):
  3.     if 满足结束条件:
  4.         result.append(路径)
  5.         return
  7.     for 选择 in 选择列表:
  8.         # 为了结果不重复，一般得加下面这个判断
  9.         if i > 0 and num[i] == num[i-1]:
  10.             continue
  11.         # 做选择
  12.         路径.append(选择)
  14.         dfs(路径, 选择列表)
  16.         # 撤销选择
  17.         路径.pop(选择)

核心：就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」。写 backtrack 函数时，需要维护走过的「路径」和当前可以做的「选择列表」，当触发「结束条件」时，将「路径」记入结果集。

无重复列表全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

  1. class Solution(object):
  2.     def permute(self, nums):
  3.         # 方法一：套模版，需要撤销
  4.         # 定义全局变量保存最终结果
  5.         res = [] 
  6.         # 定义状态变量保存当前状态
  7.         path = [] 
  9.         def dfs(nums, path):
  10.             # 结束条件
  11.             if len(path) == len(nums):
  12.                 res.append(path[:])           
  13.             for i in nums:
  14.                 # 如果在当前排列中已经有i了，就continue，相当于分支限界，即不对当前节点子树搜寻了
  15.                 if i in path: 
  16.                     continue  
  17.                 # 做选择
  18.                 path.append(i)
  19.                 dfs(nums, path)
  20.                 # 撤销选择
  21.                 path.pop()
  22.         dfs(nums, path)
  23.         return res
  25.         # 方法二：不撤销，运用另一套模版
  26.         res = [] 
  27.         path = [] 
  29.         def dfs(nums, path):
  30.             if len(path) == len(nums):
  31.                 res.append(path[:])
  32.             for i in nums:
  33.                 # 如果在当前排列中已经有i了，就continue，相当于分支限界，即不对当前节点子树搜寻了
  34.                 if i in path: 
  35.                     continue
  36.                 dfs(nums, path + [i])
  37.         dfs(nums, path)
  38.         return res

有重复列表全排列

给定一个可包含重复数字的序列，返回所有不重复的全排列。
输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]

  1. class Solution(object):
  2.     def permuteUnique(self, nums):
  3.         res = []
  4.         path = []
  5.         # 务必记录长度
  6.         n = len(nums)
  8.         def dfs(nums, path):
  9.              # 需要满足条件才能append，也就长度得是3，还不能重复
  10.             if len(path)==n and path not in res:
  11.                 res.append(path[:])
  12.             for i in range(len(nums)):
  13.                 # 由于题目数据有重复，所以得pass
  14.                 if i > 0 and nums[i] == nums[i-1]:
  15.                     continue            
  16.                 # 将当前遍历到的元素删除
  17.                 dfs(nums[:i] + nums[i+1:], path + [nums[i]])
  18.         dfs(nums, path)
  19.         return res

无重复字符串的排列组合

无重复字符串的排列组合。编写一种方法，计算某字符串的所有排列组合，字符串每个字符均不相同。
输入：S = “qwe”
输出：[“qwe”, “qew”, “wqe”, “weq”, “ewq”, “eqw”]
输入：S = “ab”
输出：[“ab”, “ba”]

  1. # 待定
  2. class Solution(object):
  3.     def permutation(self, S):
  4.         nums = S
  5.         res = [] 
  6.         path = [] 
  8.         def dfs(nums, path):
  9.             if len(path) == len(nums):
  10.                 res.append(''.join(path))
  11.             for i in nums:
  12.                 # 如果在当前排列中已经有i了，就continue，相当于分支限界，即不对当前节点子树搜寻了
  13.                 if i in path: 
  14.                     continue
  15.                 dfs(nums, path + [i])
  16.         dfs(nums, path)
  17.         return res

有重复字符串的排列组合

有重复字符串的排列组合。编写一种方法，计算某字符串的所有排列组合。
输入：S = “qqe”
输出：[“eqq”,”qeq”,”qqe”]
输入：S = “ab”
输出：[“ab”, “ba”]

  1. class Solution(object):
  2.     def permutation(self, S):    
  3.         # 方法一：比较好理解，和上面的列表全排列类似
  4.         nums = list(sorted(S))
  5.         res = []
  6.         path = []
  7.         # 务必记录长度
  8.         n = len(nums)
  10.         def dfs(nums, path):
  11.             # 需要满足条件才能append，也就长度得是3，还不能重复
  12.             if len(path)==n and ''.join(path) not in res:
  13.                 res.append(''.join(path))
  14.             for i in range(len(nums)):
  15.                 # 由于题目数据有重复，所以得pass
  16.                 if i > 0 and nums[i] == nums[i-1]:
  17.                     continue            
  18.                 # 将当前遍历到的元素删除
  19.                 dfs(nums[:i] + nums[i+1:], path + [nums[i]])
  20.         dfs(nums, path)
  21.         return res    
  24.         # 方法二：需要用散列表去重，不太好理解
  25.         s = list(s)
  26.         res = []
  28.         def dfs(x):
  29.             if x == len(s) - 1:
  30.                 res.append(''.join(s)) # 添加排列方案
  31.                 return
  32.             dicts = {}
  33.             for i in range(x, len(s)):
  34.                 if s[i] in dicts: 
  35.                     continue # 重复，因此剪枝
  36.                 dicts[s[i]] = i
  37.                 s[i], s[x] = s[x], s[i] # 交换，将 s[i] 固定在第 x 位
  38.                 dfs(x + 1) # 开启固定第 x + 1 位字符
  39.                 s[i], s[x] = s[x], s[i] # 恢复交换
  40.         dfs(0)
  41.         return res

无重复子集

给你一个整数数组 nums ，数组中的元素互不相同 。返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
输入：nums = [0]
输出：[[],[0]]

  1. class Solution(object):
  2.     def subsets(self, nums):
  3.         res = []
  4.         path = []
  5.         def dfs(nums, index):
  6.             # 因为长的短的都要，所以append放外面了
  7.             res.append(path[:])
  8.             if len(path) == len(nums):
  9.                 return
  11.             for i in range(index, len(nums)):
  12.                 path.append(nums[i])
  13.                 dfs(nums, i+1)
  14.                 path.pop()
  15.         dfs(nums, 0)
  16.         return res

有重复子集

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]
输入：nums = [0]
输出：[[],[0]]

  1. class Solution(object):
  2.     def subsetsWithDup(self, nums):
  3.         res = []
  4.         path = []
  5.         # 和上一题的第一个区别就是需要排序
  6.         nums.sort()
  8.         def dfs(nums, index):
  9.             # 因为长的短的都要，所以append放外面了
  10.             res.append(path[:])
  11.             if len(path) == len(nums) and path not in res:
  12.                 return 
  14.             for i in range(index, len(nums)):
  15.                 # 由于题目数据有重复，所以得pass
  16.                 if i > index and nums[i] == nums[i-1]:
  17.                     continue
  18.                 path.append(nums[i])
  19.                 dfs(nums, i+1)
  20.                 path.pop()
  21.         dfs(nums, 0)
  22.         return res

电话号码的字母组合（无重复类型）

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
输入：digits = “23”
输出：[“ad”,”ae”,”af”,”bd”,”be”,”bf”,”cd”,”ce”,”cf”]
输入：digits = “”
输出：[]
输入：digits = “2”
输出：[“a”,”b”,”c”]

  1. class Solution(object):
  2.     def letterCombinations(self, digits):
  3.         if digits == "":
  4.             return []
  6.         dicts = {"2": "abc", "3": "def", "4": "ghi", "5": "jkl", "6": "mno", "7": "pqrs", "8": "tuv", "9": "wxyz"}
  7.         res = []
  8.         path = ""
  10.         def dfs(index, path):
  11.             # 如果目前path的长度和digits的长度相等，说明已经遍历完一趟，返回结果列表
  12.             if len(path) == len(digits):
  13.                 res.append(path)
  14.                 return
  16.             # 遍历当前索引的数字对应的英文列表
  17.             for i in dicts[digits[index]]:
  18.                 # 递归下一个数字对应的英文列表
  19.                 dfs(index+1, path+i)
  21.         dfs(0, path)
  22.         return res

整数的所有组合（无重复类型）

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

  1. class Solution(object):
  2.     def combine(self, n, k):
  3.         res = []
  4.         path = []
  5.         # 两个参数，一个是从1开始一直加到n的整数，一个是暂存的列表。
  6.         def dfs(index, path):
  7.             if len(path) == k:
  8.                 res.append(path[:])
  9.                 return
  11.             # 如果列表长度小于k的话，就进入循环，将j增大1，且暂存列表加入数字j
  12.             for j in range(index, n+1):
  13.                 dfs(j+1, path+[j])
  15.         dfs(1, path)
  16.         return res

括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。
输入：n = 3
输出：[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]

  1. class Solution:
  2.     def generateParenthesis(self, n):
  3.         # 先把所有组合给生成出来，即DFS所有节点，发现有一些结果是我们不需要的，比如((((，比如))))
  4.         if n <= 0: 
  5.             return []
  6.         res = []
  8.         def dfs(paths):
  9.             if len(paths) == n * 2:  # 因为括号都是成对出现的
  10.                 res.append(paths)
  11.                 return
  12.             # 这时我增加了left与right参数，分别代表左括号与右括号的数量，每生成一个我就增加一个。
  13.             dfs(paths + '(')
  14.             dfs(paths + ')')
  16.         dfs('')
  17.         return res
  19. ## 上面是全排列，下面添加剪枝条件
  20. class Solution:
  21.     def generateParenthesis(self, n):  
  22.         if n <= 0: 
  23.             return []
  24.         res = []
  26.         def dfs(paths, left, right):
  27.             if left > n or right > left: 
  28.                 return
  29.             if len(paths) == n * 2:  # 因为括号都是成对出现的
  30.                 res.append(paths)
  31.                 return
  33.             dfs(paths + '(', left + 1, right)
  34.             dfs(paths + ')', left, right + 1)
  35.         dfs('', 0, 0)
  36.         return res

有效的括号（不是DFS，属于栈）

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串 s ，判断字符串是否有效。
有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
输入：s = “()”
输出：true
输入：s = “()[]{}”
输出：true
输入：s = “(]”
输出：false

  1. class Solution(object):
  2.     def isValid(self, s):
  3.         stack = []
  4.         left = ['{', '[', '(']
  5.         for c in s:
  6.             if c in left:
  7.                 stack.append(c)
  8.             else:
  9.                 if not stack:
  10.                     return False
  11.                 temp = stack.pop()
  12.                 if c == ')':
  13.                     if temp != '(':
  14.                         return False
  15.                 if c == ']':
  16.                     if temp != '[':
  17.                         return False
  18.                 if c == '}':
  19.                     if temp != '{':
  20.                         return False
  21.         return stack == []

最长有效括号（不是DFS，属于栈）

给你一个只包含 ‘(‘ 和 ‘)’ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。
输入：s = “(()”
输出：2
解释：最长有效括号子串是 “()”
输入：s = “)()())”
输出：4
解释：最长有效括号子串是 “()()”

  1. class Solution(object):
  2.     def longestValidParentheses(self, s):
  3.         # 压栈
  4.         if not s:
  5.             return 0
  6.         res = 0
  7.         # 入栈条件为1.栈为空 2.当前字符是'(' 3.栈顶符号位')'，因为三种条件都没办法消去成对的括号。
  8.         stack = [-1]
  9.         for i in range(len(s)):
  10.             if s[i] == "(":
  11.                 stack.append(i)
  12.             else:
  13.                 stack.pop()
  14.                 if not stack:
  15.                     stack.append(i) 
  16.                 else:
  17.                     res = max(res, i-stack[-1])
  18.         return res

矩阵中的路径

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。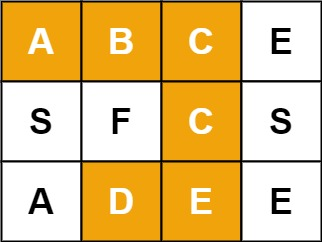
image.png
例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。
输入：board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCCED”
输出：true
输入：board = [[“a”,”b”],[“c”,”d”]], word = “abcd”
输出：false

  1. class Solution(object):
  2.     def exist(self, board, word):
  3.         def dfs(board, i, j, word):
  4.             if len(word) == 0:  # 如果单词已经检查完毕
  5.                 return True
  6.             # 如果路径出界或者矩阵中的值不是word的首字母，返回False
  7.             if i < 0 or i >= len(board) or j < 0 or j >= len(board[0]) or word[0] != board[i][j]:
  8.                 return False
  9.             # 标记一下，代表此元素已访问过，防止之后搜索时重复访问。
  10.             tmp = board[i][j]
  11.             board[i][j] = '#'
  13.             # 上下左右四个方向搜索
  14.             res = dfs(board, i+1, j, word[1:]) or dfs(board, i-1, j, word[1:]) or dfs(board, i, j+1, word[1:]) or dfs(board, i, j-1, word[1:])
  16.             # 还原当前矩阵元素
  17.             board[i][j] = tmp
  18.             return res
  20.         for i in range(len(board)):
  21.             for j in range(len(board[0])):
  22.                 if dfs(board, i, j, word):
  23.                     return True
  24.         return False

岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外，你可以假设该网格的四条边均被水包围。
输入：grid = [
[“1”,”1”,”1”,”1”,”0”],
[“1”,”1”,”0”,”1”,”0”],
[“1”,”1”,”0”,”0”,”0”],
[“0”,”0”,”0”,”0”,”0”]
]
输出：1
输入：grid = [
[“1”,”1”,”0”,”0”,”0”],
[“1”,”1”,”0”,”0”,”0”],
[“0”,”0”,”1”,”0”,”0”],
[“0”,”0”,”0”,”1”,”1”]
]
输出：3

  1. class Solution(object):
  2.     def numIslands(self, grid):
  3.         # 方法一：深度优先遍历DFS，这种好理解
  4.         def dfs(grid, i, j):
  5.             if not 0 <= i < len(grid) or not 0 <= j < len(grid[0]) or grid[i][j] == '0': 
  6.                 return
  7.             # 将岛屿所有节点删除，以免之后重复搜索相同岛屿
  8.             grid[i][j] = '0'
  9.             dfs(grid, i + 1, j)
  10.             dfs(grid, i, j + 1)
  11.             dfs(grid, i - 1, j)
  12.             dfs(grid, i, j - 1)
  13.         count = 0
  14.         for i in range(len(grid)):
  15.             for j in range(len(grid[0])):
  16.                 if grid[i][j] == '1':
  17.                     # 从 (i, j) 向此点的上下左右 (i+1,j),(i-1,j),(i,j+1),(i,j-1) 做深度搜索
  18.                     dfs(grid, i, j)
  19.                     count += 1
  20.         return count
  22.         # 方法二：广度优先遍历 BFS
  23.         def bfs(grid, i, j):
  24.             queue = [[i, j]]
  25.             while queue:
  26.                 [i, j] = queue.pop(0)
  27.                 if 0 <= i < len(grid) and 0 <= j < len(grid[0]) and grid[i][j] == '1':
  28.                     grid[i][j] = '0'
  29.                     queue += [[i + 1, j], [i - 1, j], [i, j - 1], [i, j + 1]]
  30.         count = 0
  31.         for i in range(len(grid)):
  32.             for j in range(len(grid[0])):
  33.                 if grid[i][j] == '0': 
  34.                     continue
  35.                 bfs(grid, i, j)
  36.                 count += 1
  37.         return count

迷路的机器人

设想有个机器人坐在一个网格的左上角，网格 r 行 c 列。机器人只能向下或向右移动，但不能走到一些被禁止的网格（有障碍物）。设计一种算法，寻找机器人从左上角移动到右下角的路径。网格中的障碍物和空位置分别用 1 和 0 来表示。
输入:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
输出: [[0,0],[0,1],[0,2],[1,2],[2,2]]

  1. class Solution(object):
  2.     def pathWithObstacles(self, obstacleGrid):
  3.         stack = []
  4.         m, n = len(obstacleGrid), len(obstacleGrid[0])
  5.         # 主要思路是压栈
  6.         def dfs(x, y):
  7.             # 出界或者走到障碍物
  8.             if x < 0 or x == n or y < 0 or y == m or obstacleGrid[y][x] == 1:
  9.                 return False
  11.             # 添加到总路径，并标记为走过
  12.             obstacleGrid[y][x] = 1
  13.             stack.append([y, x])
  15.             # 如果走到终点了就直接返回True
  16.             if x == n - 1 and y == m - 1:
  17.                 return True
  19.             # 向右走
  20.             if dfs(x + 1, y): 
  21.                 return True
  22.             # 向左走
  23.             if dfs(x, y + 1): 
  24.                 return True
  26.             # 如果在上面都没有被return，那么清除刚添加的总路径，并返回False
  27.             stack.pop() 
  28.             return False
  30.         dfs(0, 0)
  31.         return stack

迷宫

  1. mete = [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
  2.         [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
  3.         [1, 0, 0, 1, 0, 1, 0, 1, 0, 1],
  4.         [1, 0, 1, 0, 0, 0, 0, 1, 0, 1],
  5.         [1, 0, 1, 0, 1, 0, 1, 1, 0, 1],
  6.         [1, 0, 0, 0, 1, 1, 1, 1, 0, 1],
  7.         [1, 0, 1, 0, 0, 0, 0, 0, 0, 1],
  8.         [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
  11. class Solution(object):
  12.     # 方法一：深度优先，但是不是最优解
  13.     def dfs_stack(self, start, end, mete):
  14.         stack = [start]
  15.         while stack:
  16.             now = stack[-1]
  17.             if now == end:
  18.                 print(stack)
  19.                 return True
  20.             x, y = now
  21.             mete[x][y] = 2
  22.             if mete[x - 1][y] == 0:
  23.                 stack.append([x - 1, y])
  24.                 continue
  25.             elif mete[x][y - 1] == 0:
  26.                 stack.append([x, y - 1])
  27.                 continue
  28.             elif mete[x + 1][y] == 0:
  29.                 stack.append([x + 1, y])
  30.                 continue
  31.             elif mete[x][y + 1] == 0:
  32.                 stack.append([x, y + 1])
  33.                 continue
  34.             else:
  35.                 stack.pop()
  36.         return False
  38.     # 方法二：广度优先，最优解
  39.     def bfs_queue(self, start, end, mete):
  40.         def dfs(next_x, next_y):
  41.             if mete[next_x][next_y] == 0:
  42.                 queue.append([next_x, next_y, len(tmp) - 1]) # 如果不统计路径，这个len(tmp) - 1就没用
  43.                 mete[next_x][next_y] = 2
  45.         x1, y1 = start
  46.         queue = [[x1, y1, -1]]  # 如果不统计路径，这个1就没用
  47.         mete[x1][y1] = 2
  48.         tmp = []
  49.         while queue:
  50.             now = queue.pop(0)
  51.             tmp.append(now)
  53.             if now[0:2] == end:
  54.                 # 这段代码统计路径路径
  55.                 # path = []
  56.                 # i = len(tmp) - 1
  57.                 # while i >= 0:
  58.                 #     path.append(tmp[i][0:2])
  59.                 #     i = tmp[i][2]
  60.                 # path = path[::-1]
  61.                 # print(path)
  62.                 return True
  64.             dfs(now[0] - 1, now[1])
  65.             dfs(now[0], now[1] + 1)
  66.             dfs(now[0] + 1, now[1])
  67.             dfs(now[0], now[1] - 1)
  68.         else:
  69.             return False
  72. start = [1, 1]
  73. end = [6, 8]
  74. A = Solution()
  75. print(A.bfs_queue(start, end, mete))
  76. print(A.dfs_stack(start, end, mete))