好烦……各种排序各种忘…..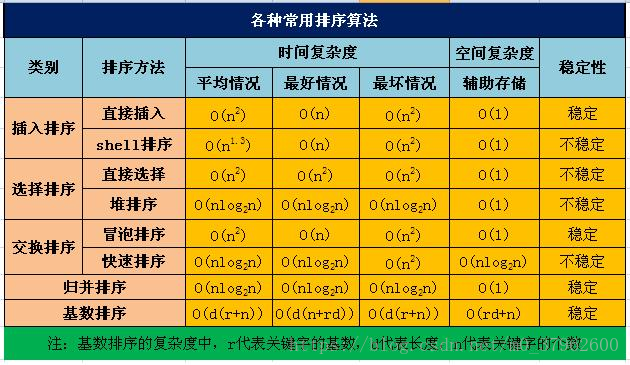
image.png

排序的算法比较常见的有： 冒泡排序 快速排序 归并排序 插入排序 堆排序
�

冒泡排序：

基本上科班出身的秃头们，学的第一个算法就是冒泡排序吧…..可能是名字比较好听，咕噜咕噜的
核心思想：冒泡的核心思想就是，两两相比较，比较相邻的两个位置元素的大小。基本入手点就是双重for循环
但是经常我们会搞错了冒泡，看下面的代码

  1. func test(nums []int) (ret []int) {
  2.     swap := func(nums []int,i,j int) []int {
  3.         num := nums[i]
  4.         nums[i] = nums[j]
  5.         nums[j] = num
  6.         return nums
  7.     }
  8.     for i := 0; i < len(nums); i++ {
  9.         for j := i+1; j < len(nums); j++ {
  10.             if nums[i] > nums[j] {
  11.                 nums = swap(nums,i,j)
  12.             }
  13.         }
  14.     }
  15.     return nums
  16. }

这个是你所想的冒泡嘛？ 错！！！大错特错了….冒泡排序的核心思想是相邻的两个位置相比较嘛，所以是这样的

  1. func maopao(nums []int) (ret []int) {
  2.     swap := func(nums []int,i,j int) []int {
  3.         num := nums[i]
  4.         nums[i] = nums[j]
  5.         nums[j] = num
  6.         return nums
  7.     }
  8.     flag := true
  9.     for i := 0; i < len(nums) && flag; i++ {
  10.         flag = false
  11.         for j := 0; j < len(nums)-i-1; j++ {
  12.             if nums[j] > nums[j+1] {
  13.                 nums = swap(nums,j,j+1)
  14.                 flag = true
  15.             }
  16.         }
  17.     }
  18.     return nums
  19. }

快速排序:

快排一般是有关面试算法的必问题….唉…..
核心思想：基准数 从数组中选择一个基准数（一般是最开头的内个元素）让其他比基准数小的元素移动到一边，大的移动另一边。 在对左右两边的区间重复上一次操作，直到区间中剩下一个元素

快速排序和归并排序 其实用到的都是分治法的思想，但是却有所不同。归并排序是自下而上的，先处理子问题，然后再合并，将小集合合成大集合，最后实现排序。而快速排序是由上到下的，先分区，然后再处理子问题。

下面代码实现
（递归版）

  1. func kuaipai(nums []int) []int {
  2.     //比较置换
  3.     swap := func(nums []int,i,j int) {
  4.         num := nums[i]
  5.         nums[i] = nums[j]
  6.         nums[j] = num
  7.     }
  8.     //选出基准数，进行分区
  9.     partition := func(nums []int,left,right int) int{
  10.         start := left
  11.         left++
  12.         for left < right {
  13.             for left < right && nums[left] < nums[start] {
  14.                 left++
  15.             }
  16.             for left < right && nums[right] > nums[start] {
  17.                 right--
  18.             }
  19.             if left >= right {
  20.                 break
  21.             }
  22.             swap(nums,left,right)
  23.         }
  24.         //如果当前值比基准元素还大，那将基本元素和当前值的前一位置换
  25.         if nums[right] > nums[start] {
  26.             right--
  27.         }
  28.         swap(nums,start,right)
  29.         return right
  30.     }
  31.     var sort func(nums []int,left,right int)
  32.     sort = func(nums []int,left,right int) {
  33.         if left < right {
  34.             par := partition(nums, left, right)
  35.             sort(nums,left,par-1)
  36.             sort(nums,par+1,right)
  37.         }
  38.     }
  39.     sort(nums,0,len(nums)-1)
  40.     return nums
  41. }

一般升级版算法题，不让你用递归….所以需要用“栈” 利用栈的先进后出的特点， 找寻基准数，并分区的方法不变，将原来的递归改成压栈

（非递归版）

  1. func kuaipaiFDG(nums []int) []int {
  2.     //比较置换
  3.     swap := func(nums []int,i,j int) {
  4.         num := nums[i]
  5.         nums[i] = nums[j]
  6.         nums[j] = num
  7.     }
  8.     //选出基准数，进行分区
  9.     partition := func(nums []int,left,right int) int{
  10.         start := left
  11.         left++
  12.         for left < right {
  13.             for left < right && nums[left] < nums[start] {
  14.                 left++
  15.             }
  16.             for left < right && nums[right] > nums[start] {
  17.                 right--
  18.             }
  19.             if left >= right {
  20.                 break
  21.             }
  22.             swap(nums,left,right)
  23.         }
  24.         //如果当前值比基准元素还大，那将基本元素和当前值的前一位置换
  25.         if nums[right] > nums[start] {
  26.             right--
  27.         }
  28.         swap(nums,start,right)
  29.         return right
  30.     }
  31.     //使用栈，栈里存储这每一次基准数的分区区间 每一次弹栈出来一个区间，在继续寻找基准数，区分分区...以此类推，直到每一个分区都是一个元素
  32.     var stack []int
  33.     //先把起始和结束放进去
  34.     stack = append(stack,0)
  35.     stack = append(stack,len(nums)-1)
  37.     for len(stack) != 0 {
  38.         right := stack[len(stack)-1]
  39.         stack = stack[:len(stack)-1]
  40.         left := stack[len(stack)-1]
  41.         stack = stack[:len(stack)-1]
  42.         if left < right {
  43.             par := partition(nums,left,right)
  44.             //压栈
  45.             stack = append(stack,left)
  46.             stack = append(stack,par-1)
  47.             stack = append(stack,par+1)
  48.             stack = append(stack,right)
  49.         }
  50.     }
  51.     return nums
  52. }

快排是可以优化的…我们在寻找基准数的时候，都是默认区间内的第一个.这样在极端的情况下，效率很低，可以用三数取中法啥的…这个自己看看吧，看太多也都记不住…

归并排序

归并排序也是必须掌握的排序算法….上面也说了它和快排都是采用分治法，但是又略有不用
核心思想：分治法, 不同于快排的是 它是先处理子问题，在合并成分区..也就是说把一个长度为N的数组，分割成N个子序列，长度为1 。之后两两归并成一个排好序的区间，这样最后归并成一个区间，

放一个图吧..网上找的，就更好了理解了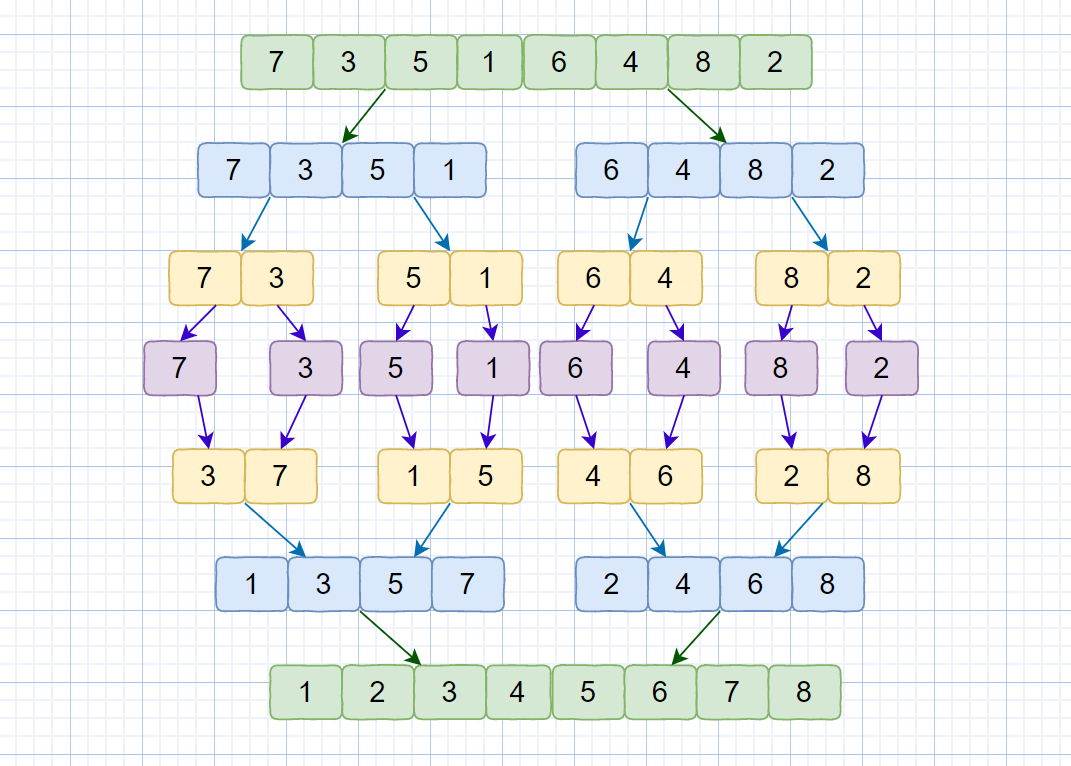
image.png
下面代码实现
（递归版）

  1. func guibingDG(nums []int) []int {
  2.     merge := func(nums []int, left,right,mid int) {
  3.         //首选，创建一个存储归并后的大集合数组
  4.         var mergeNums []int
  5.         //其次，用两个指针，分别在两个区间内比较，归并两个区间
  6.         tmp,tmp1 := left,mid+1
  7.         for tmp <= mid || tmp1 <= right {
  8.             if tmp > mid {
  9.                 mergeNums = append(mergeNums,nums[tmp1])
  10.                 tmp1++
  11.                 continue
  12.             }
  13.             if tmp1 > right {
  14.                 mergeNums = append(mergeNums,nums[tmp])
  15.                 tmp++
  16.                 continue
  17.             }
  18.             //俩俩比较落入新的集合数组
  19.             if nums[tmp] <= nums[tmp1] {
  20.                 mergeNums = append(mergeNums,nums[tmp])
  21.                 tmp++
  22.             }else {
  23.                 mergeNums = append(mergeNums,nums[tmp1])
  24.                 tmp1++
  25.             }
  26.         }
  27.         //最后，将大集合 还原到原先数组中
  28.         index := 0
  29.         for i := left; i <= right && len(mergeNums) > 0; i++ {
  30.             nums[i] = mergeNums[index]
  31.             index++
  32.         }
  33.     }
  34.     var sort func(nums []int, left,right int)
  35.     sort = func(nums []int, left,right int) {
  36.         if left < right {
  37.             mid := left + (right-left) / 2
  38.             sort(nums,left,mid)
  39.             sort(nums,mid+1,right)
  40.             merge(nums,left,right,mid)
  41.         }
  42.     }
  43.     sort(nums,0,len(nums)-1)
  44.     return nums
  45. }

（非递归版）merge归并方法都是一样的，只不过非递归版本是用变量标志子集的长度大小

  1. func guibingFDG(nums []int) []int {
  2.     merge := func(nums []int, left,right,mid int) {
  3.         //首选，创建一个存储归并后的大集合数组
  4.         var mergeNums []int
  5.         //其次，用两个指针，分别在两个区间内比较，归并两个区间
  6.         tmp,tmp1 := left,mid+1
  7.         for tmp <= mid || tmp1 <= right {
  8.             if tmp > mid {
  9.                 mergeNums = append(mergeNums,nums[tmp1])
  10.                 tmp1++
  11.                 continue
  12.             }
  13.             if tmp1 > right {
  14.                 mergeNums = append(mergeNums,nums[tmp])
  15.                 tmp++
  16.                 continue
  17.             }
  18.             //俩俩比较落入新的集合数组
  19.             if nums[tmp] <= nums[tmp1] {
  20.                 mergeNums = append(mergeNums,nums[tmp])
  21.                 tmp++
  22.             }else {
  23.                 mergeNums = append(mergeNums,nums[tmp1])
  24.                 tmp1++
  25.             }
  26.         }
  27.         //最后，将大集合 还原到原先数组中
  28.         index := 0
  29.         for i := left; i <= right && len(mergeNums) > 0; i++ {
  30.             nums[i] = mergeNums[index]
  31.             index++
  32.         }
  33.     }
  34.     k := 1  //子集合大小 1，2，4，8....
  35.     for k < len(nums) {
  36.         var i int
  37.         for i = 0; i < len(nums)-2*k; i += 2*k {
  38.             merge(nums,i,i+2*k-1,i+k-1)
  39.         }
  40.         if  i+k < len(nums) {
  41.             merge(nums,i,len(nums)-1,i+k-1)
  42.         }
  43.         k = 2*k
  44.     }
  45.     return nums
  46. }


插入排序：

插入排序也算是基础算法中的一种了..感觉不是咋常用….
核心思想： 将一个元素插入到已经排好序的序列中，得到一个新的序列。 也就是说我们要将原序列分成两个区间，有序区间和无序区间，每次从无序区间中取一个，插入到有序区间

直接上代码吧..

  1. func charu(nums []int) []int {
  2.     //把第一个元素当做是有序区间 , 所以i=1 从1开始
  3.     for i := 1; i < len(nums); i++ {
  4.         tmp := nums[i]
  5.         var j int
  6.         //有序区间从后往前，和元素比较并移动位置，为元素腾地方
  7.         for j = i - 1; j >= 0; j-- {
  8.             if tmp < nums[j] {
  9.                 nums[j+1] = nums[j]
  10.                 continue
  11.             }
  12.             break
  13.         }
  14.         //归位
  15.         nums[j+1] = tmp
  16.     }
  17.     return nums
  18. }


堆排序：

分析堆排序之前，需要知道啥玩应是堆….堆的使用场景还是非常之多的
堆的定义：

  • 必须是完全二叉树。（啥是完全二叉树？…自己百度吧..）
  • 二叉堆中的每个节点，都必须 大于等于 或者 小于等于 其子树中的每一个节点的值（顶点是最大值是大顶堆，反之是小顶堆）

因为二叉堆是完全二叉树，所以我们完全可以用数组来存储二叉堆，看图..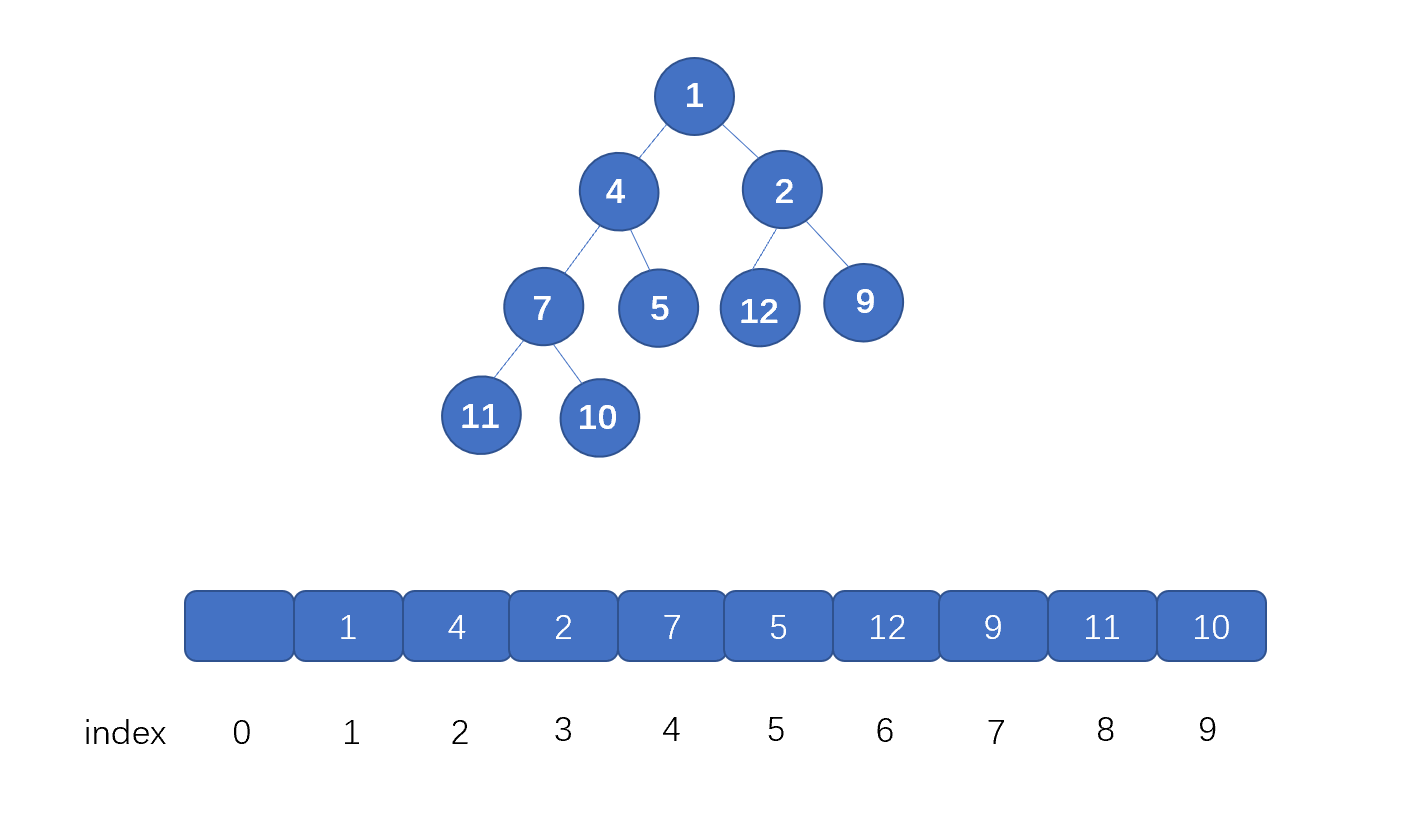
image.png
这样我们能准确的找到，每一个父节点(i) 对应的左子节点(2i) 右子节点(2i+1)的坐标…..
关键问题：如何进行堆排序？
主要分为两步骤：

  • 建堆
  • 排序

建堆的方法主要有：上浮建堆 和 下沉建堆
拿上浮建堆来说，我们每个节点的坐标是已经知道了，那我们在数组的末端要添加一个元素的话，是不是要看这个元素满足小顶堆（或大顶堆），将添加的这个元素与其父节点相比较，如果小于父节点就和其置换位置..这样一点一点该元素就上浮到自己应该在的位置

堆排序具体的执行逻辑
1.建堆，通过下沉操作建堆效率更高，具体过程是，找到最后一个非叶子节点，然后从后往前遍历执行下沉操作。
2.排序，将堆顶元素（代表最大元素）与最后一个元素交换，然后新的堆顶元素进行下沉操作，遍历执行上诉操作，则可以完成排序。

代码如下：

  1. func heap(nums []int) []int {
  2.     //比较置换
  3.     swap := func(nums []int,i,j int) {
  4.         num := nums[i]
  5.         nums[i] = nums[j]
  6.         nums[j] = num
  7.     }
  8.     //下沉建堆
  9.     sink := func(nums []int, root,end int) {
  10.         //如果该root没有左子节点了，说明下沉到位了
  11.         for 2*root <= end {
  12.             left := 2*root //左子节点的坐标
  13.             right := left+1 //右子节点的坐标
  14.             index := left
  15.             //找出root的左右两个子节点的最大值（大顶堆），之后再和当前root值比较
  16.             if  right <= end && nums[right] > nums[left]{
  17.                 index = right
  18.             }
  19.             if nums[index] > nums[root] {
  20.                 swap(nums,root,index)
  21.             }else {
  22.                 break
  23.             }
  24.             root = index
  25.         }
  26.     }
  27.     //排序 先创建一个新数组，起始位是空余节点
  28.     newNums := []int{0}
  29.     for i := 0; i < len(nums); i++ {
  30.         newNums = append(newNums,nums[i])
  31.     }
  32.     //先下沉建堆，将数组变成一个大顶堆，找出所有可能的顶点..最小的是 len(nums)/2
  33.     end := len(newNums) -1
  34.     for i := len(nums)/2; i >= 1; i-- {
  35.         sink(newNums,i,end)
  36.     }
  37.     for end > 1 {
  38.         swap(newNums,1,end)
  39.         end--
  40.         sink(newNums,1,end)
  41.     }
  42.     for i := 1; i < len(newNums); i++ {
  43.         nums[i-1] = newNums[i]
  44.     }
  45.     return nums
  46. }