背景:无信号脉冲时,我们测得的信号只有噪声,有脉冲到达时,我们测得信号是信号+噪声,这里的噪声,我们仅考虑接收设备内部的热噪声即均值为0、方差为σ^2的高斯白噪声,且噪声与信号是相互独立的。同时,我们认为数字信道化接收机数输出的信号也是一个高斯平稳过程,均值为μ,方差为σx^2。<br />原理:通过样本积累,我们知道噪声由于积累过程中的相互抵消,其均值方差积累后仍然几乎不变,但是信号积累其均值能量都会越来越大。所以通过积累后的数值再与提前设定好的门限值λth进行比较,高于门限则认为信号来了,记录下到达时刻,低于门限值则认为信号没来,不记录。<br /><br />卡方分布:x(t)是一个随机过程,每个时刻x(n)都是一个随机变量,且是股从高斯分布的,由中心极限定理可知:多个独立样本平方和的分布近似为高斯分布,所以当N取的足够大时 ,我们认为T是服从卡方分布(高斯分布)的。<br />根据卡方分布的性质,我们可以推出T的均值和方差:<br /> 通过这个表达式我们可以大致画出T的概率密度函数图像:<br />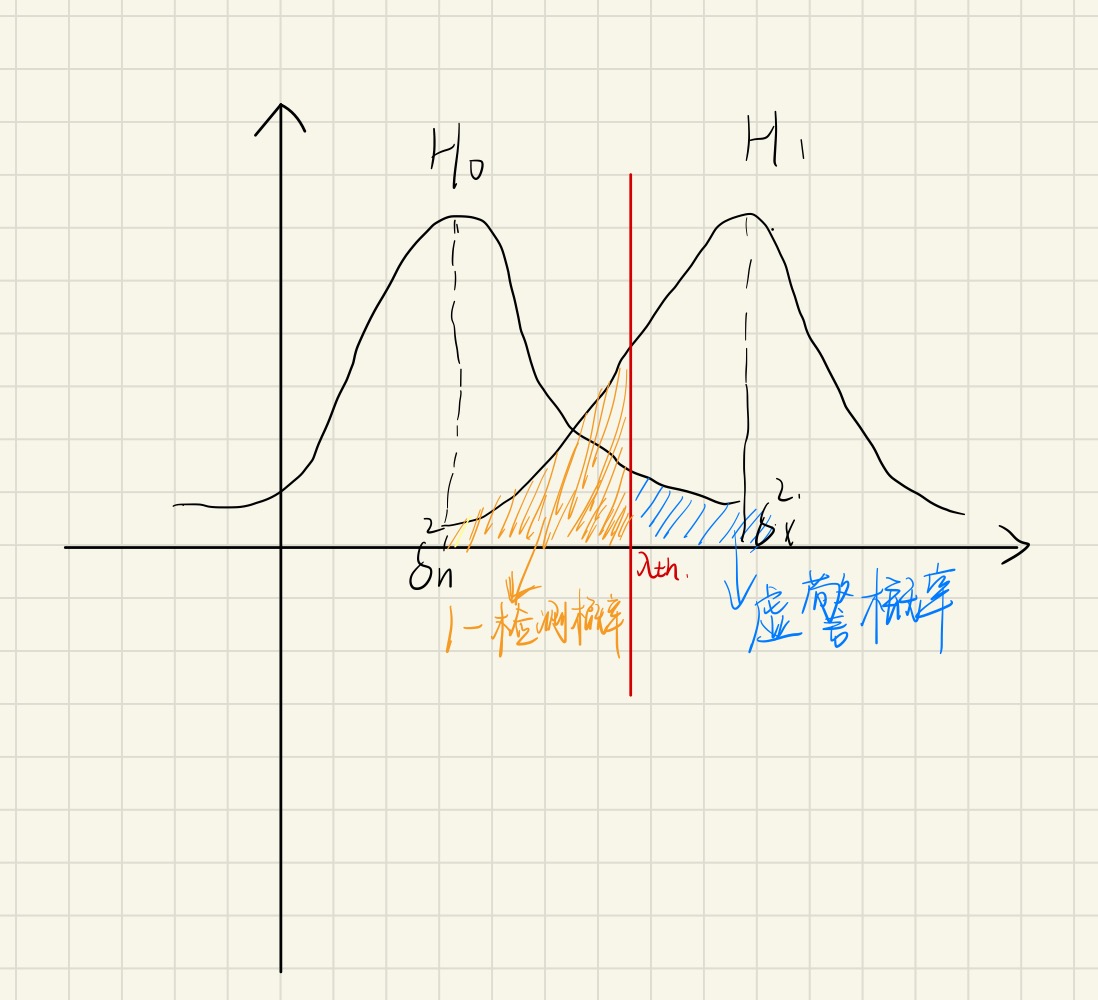<br />通过上图我们计算得到接收信号的检测概率Pd和虚警概率Pfa为:<br />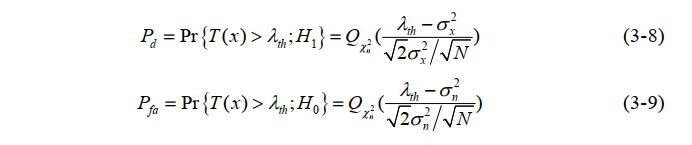<br />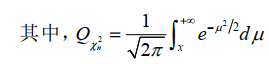<br />通过表达式,或者T的概率密度函数图我们可知,门限值λth设置的越大,虚警概率越低,但是检测概率也越低(检测灵敏度降低)。反之,门限越小,检测概率提高(检测灵敏度高),但是虚警概率也提高。根据上述关系我们列出虚警概率和检测门限的关系图,检测概率和检测门限的关系图与其一致:<br />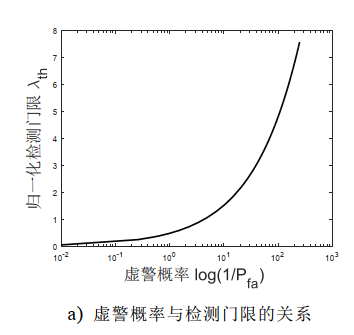<br />我们再来看一下,信噪比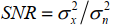检测概率之间的关系:<br />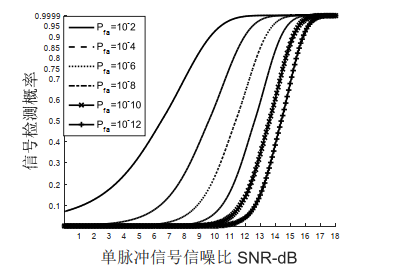<br />我们发现,虽然门限的设置会同时影响虚警概率和检测概率,但是在虚警概率一定的情况下,通过提高信噪比(T的概率密度函数H0和H1的均值间隔拉大),来提高信号检测概率。实际工程中,虚警概率是用户提出的,所以根据恒定虚警门限检测准则可以推导出我们需要设置的检测门限和检测样本的数目N:<br />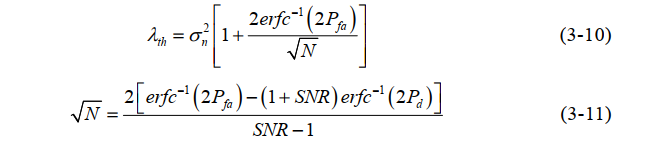<br />虚惊概率Pfa已知的情况下,要想求得门限,必须得知道N和噪声方差,要想求得N,必须知道检测概率和信噪比,检测概率可以通过信噪比和虚惊概率结合上图得到,所以关键在于求出信噪比SNR和噪声方差。如果是主动雷达,信号功率已知,我们只需要求噪声方差即可,如果是被动雷达,信号功率未知,我们需要测信噪比和噪声方差。

