背景：利用带通采样定理得到了离散的中频采样信号f（nTs），但是此数字信号是高速的，无法直接给低速的数字信号处理模块利用。需要将中频信号变到基频信号。
    定义：通过数字混频、低通滤波、数据抽取，将高速的中频信号（雷达fc+fd），转为低速的基带信号数据流（fd）。一般用正交双通道的复信号处理结构，将采样得到的实信号，变为IQ双通道的复信号，方便后面的数据处理（如匹配滤波等），也可防止频谱混叠因为I+jQ信号的频谱只有正频率部分，无负频率。
    正交混频数字下变频分类：低通滤波法，插值法，多项滤波法。
    基本原理：
    一、传统数字下变频
    1.
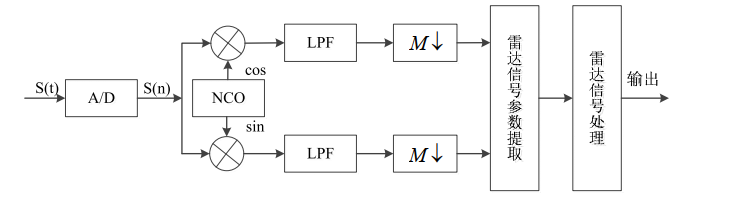
    image.png
    image.png
    image.png
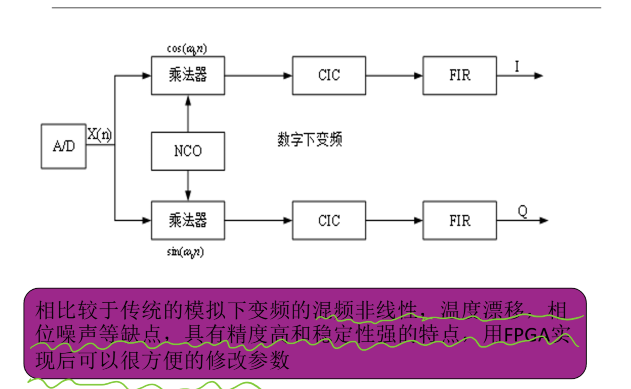
    进行低通滤波后，得到的基带信号，仍然被高速fs抽取的，所以还需要M倍抽取减少数据量。这很不经济。假设滤波完后，还剩N个采样点，则其滤波卷积运算的计算速度必须满足image.png

    2.
    image.png
    NCO：数字控制振荡器，其实就是产生离散的正弦波值，用于和采样信号S（n）（或X（n））混频，简单的NCO可以用查找表的方法获得（DDS）。
    CIC：梳妆滤波器，跟M倍抽取作用一样。是在高速抽取或者插值系统中经常使用的滤波器。N为其抽取因子。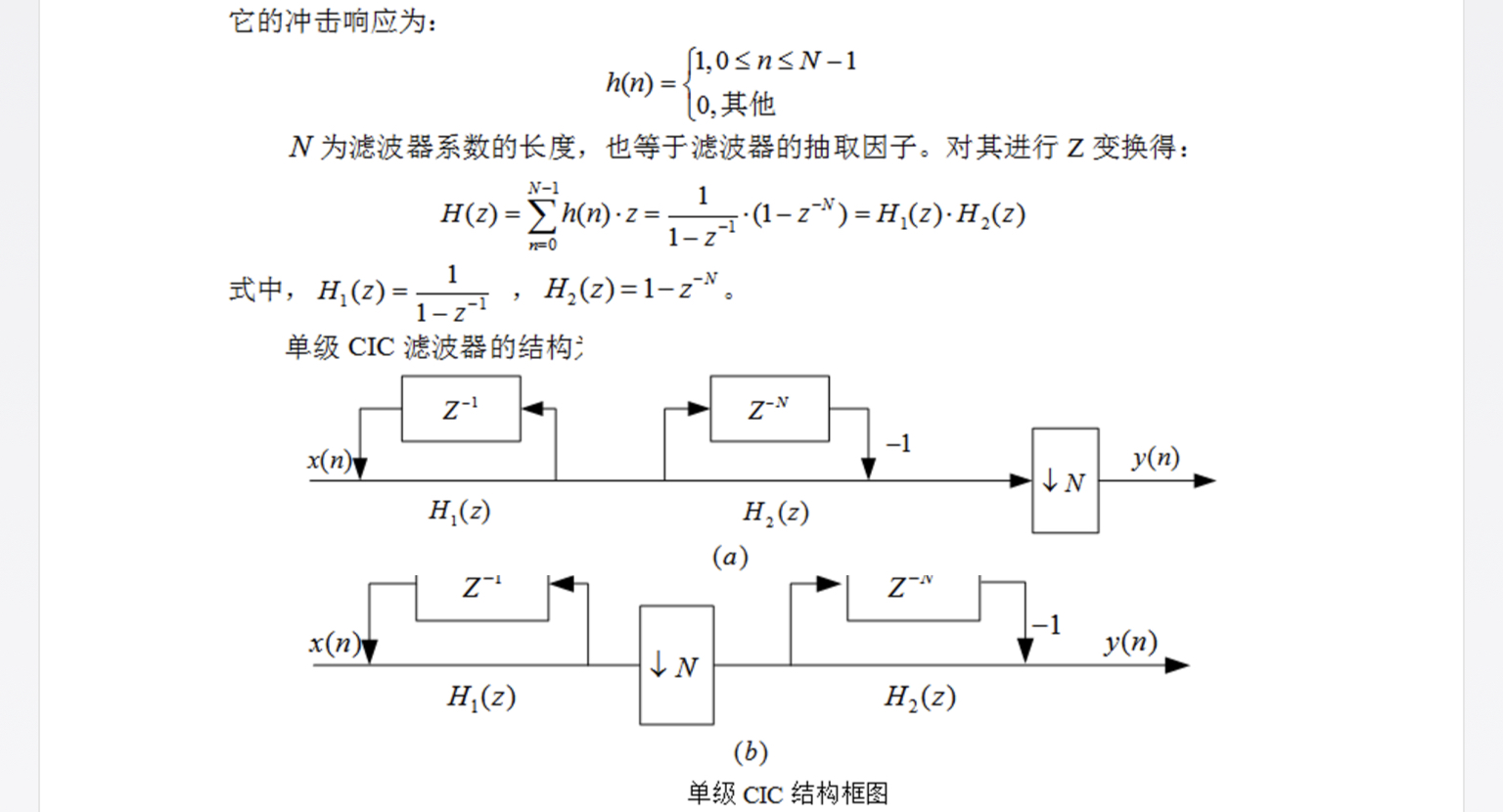
    image.png
    频谱：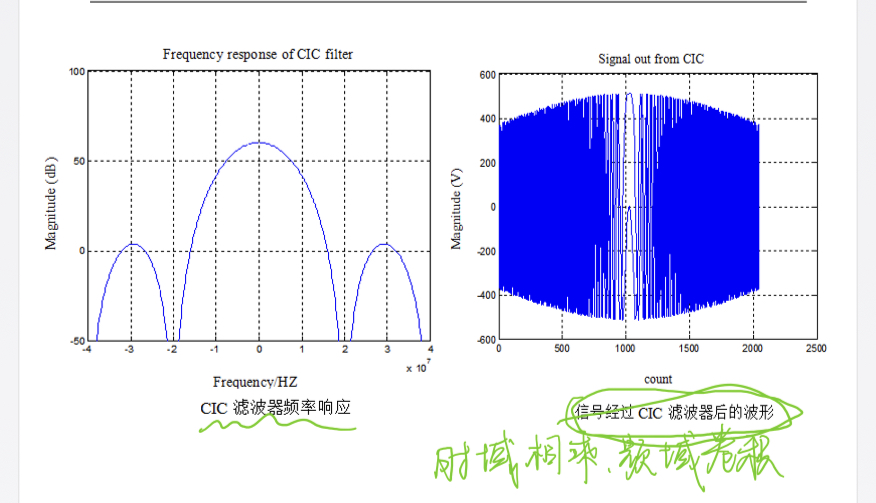
    image.png
    FIR、LFP：有限低通滤波器，去除混频之后的高频带，保留基带信号。

    二、多项滤波原理的数字下变频
    1.背景：我们知道，我们在M倍抽取前往往经过一个低通滤波器，我们可以将此滤波器分解成多个分支滤波器组，叫做多项分解，提高滤波器卷积效率和计算速度，降低滤波器的设计难度。
    2.多项分解步骤：
    FIR/LFP滤波器：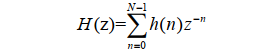
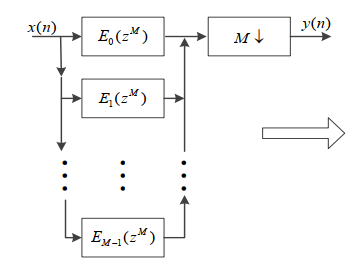
    image.png

    image.png

    image.png
    此时仍然是先滤波，再抽取，卷积后没被抽到的数据白白浪费，效率低下，根据数学关系，我们可以改变抽取和滤波的顺序，从而避免对不必要数据的滤波，同时抽取降低了给滤波器发数据的速率，降低了滤波器设计要求。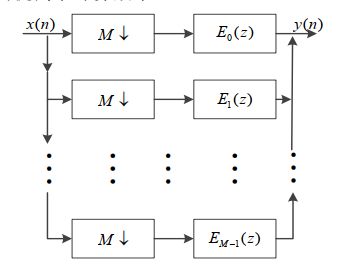
    image.png
    各分支滤波器需要满足的计算速度：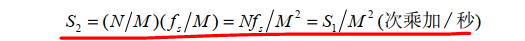
    image.png
    对分支滤波器的计算速率要求降低了M^2倍。