1、定义：将接收机所覆盖的整个频带通过使用滤波器组将其划分为多个子信道，每个信道有各自的中心频率。并且在各个子信道的输出端连接一个抽取器，这样就构成了多个低速率的子信道网络。
    2、分类

    • 低通滤波器组的数字信道化结构

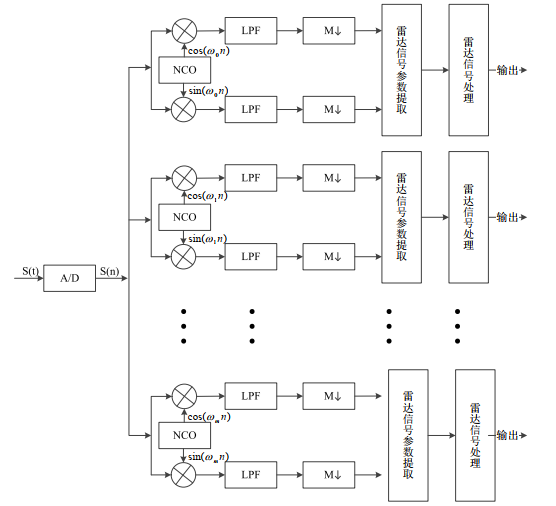
    image.png
    缺点：划分的信道越多所需的硬件资源越多。划分的信道少则测频误差大。此时中频信号直接与不同频率的调制因子进行混频，当AD采样率很高的时候，对数字混频器的工作速率要求较高。所以我们可以将抽取器中多相滤波结构的思想应用于信道化接收机当中。基于多相滤波器组的信道化结构由此产生

    • 基于多相滤波器组的信道化结构

    3、滤波器组频带划分（根据输入信号的复实和第一个子带滤波器性质划分）
    复偶划分：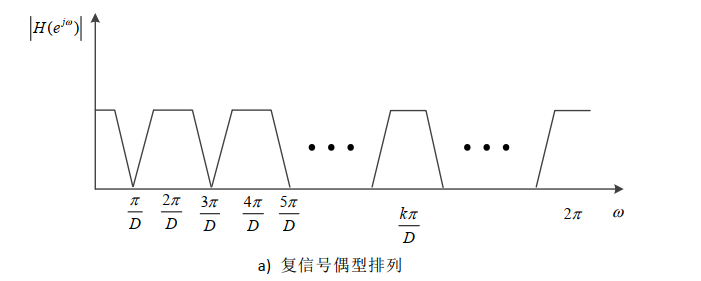
    image.png
    复实划分：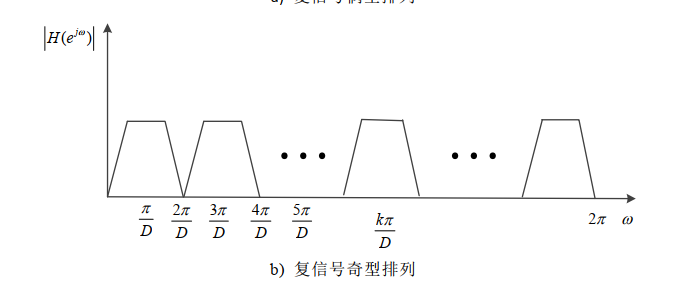
    image.png
    image.png
    实信号的频谱含有负值（-π到π），有用频带只有0-π，频带间隔仍为2π/D
    疑问1:为什么频带间隔都是按照2π/D呢？有什么依据吗？
    回答：根据采样频率fs，但是D不能太大，D大IFFT计算压力大
    实偶划分：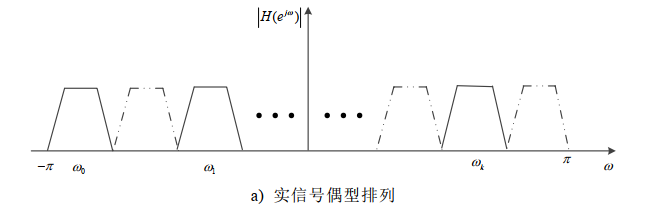
    image.png
    实奇->虚奇划分：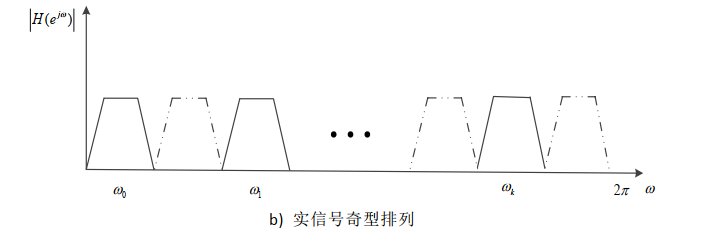
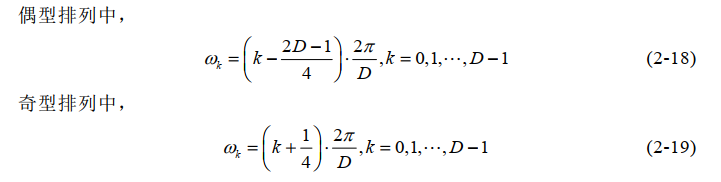
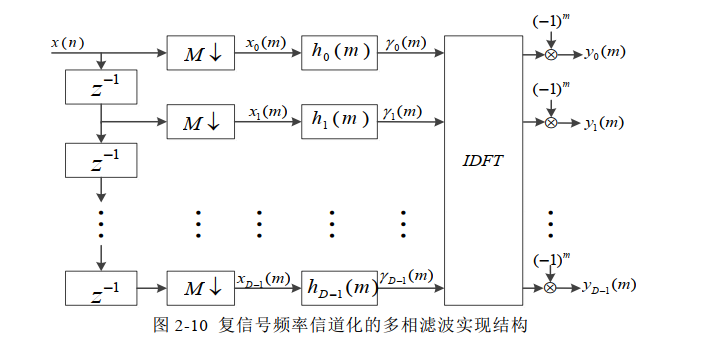
    image.png

    image.png
    4、基于多项滤波器组的高效信道化结构

    • 当输入信号为复信号时：

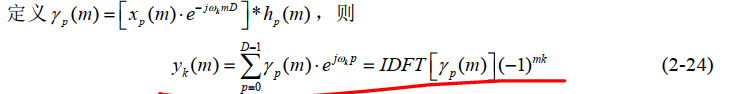
    image.png
    image.pngimage.pngimage.png
    上述公式推导存在一些小问题但是推导思路是对，IDFT少乘了前面的系数，（2-24）（-1）^mk不应该有。
    通过推导思路我们可以知道，x（n）经过抽取降速后，得到xp（n），再与原型低通滤波器的各个分支滤波器hk（m）进行卷积得到γk（m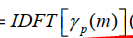）。image.png是D点的IDFT，同时γ总共有D个。
    疑问2：为什么一次D点的IFFT就可以得到全部通道的yk（m）
    image.png
    image.png
    image.png

    • 实信号输入

    实信号存在的问题：实信号的DFT变换存在负频谱及其产生的镜像频率。如果将实信号输入上述对于复信号划分的多相滤波器结构，会在对称的两个子信道输出，啥意思呢？DFT是具有隐含的周期性的，以抽样信号频率为周期，假设实信号频谱为-fm和fm，那么其-fm在搬移搬移过程中会在-fm+fs的信道出现。
    解决方法：只保留实信号的一个子信道输出结果并不会丢失信息，且该子信道的输出信号为复数形式，方便后续进行脉冲压缩等过程对雷达信号参数进行估计。
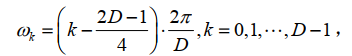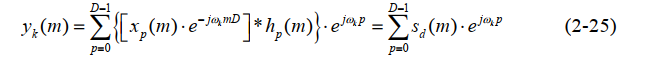
    现在假设信道化输入信号为实信号，根据实信号输入的频带划分偶型排列方式可以得到各个频带的中心频率为image.png。将这个新的ωk代入之前的式子image.png
    化简之后得到
    image.png
    image.png
    同理我们可以画出实信号的数字信道化结构：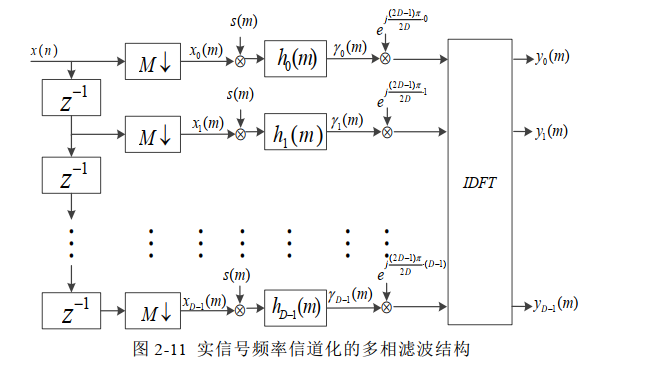
    image.png
    5、多相滤波器信道化结构的特点
    image.png
    6、避免信道中的混叠和盲区
    背景知识：滤波器都不是理想的，含有一定的过度带，所以信道划分时要考虑相邻信道间过度带的影响。滤波器带宽有两个指标：通带截止频率决定的3db带宽和阻带截止频率决定的60db带宽。通带截止频率和阻带截止频率间的频差就是过度带宽。
    设计方法：子信道60db带宽是3db带宽的两倍，处理电路的最小处理带宽必须等于60db带宽，此时相邻信道间存在至少50%的混叠。这种方法既可以避免相邻信道间的接收盲区问题，也可以避免因为信道频率间的混叠造成的测频模糊问题。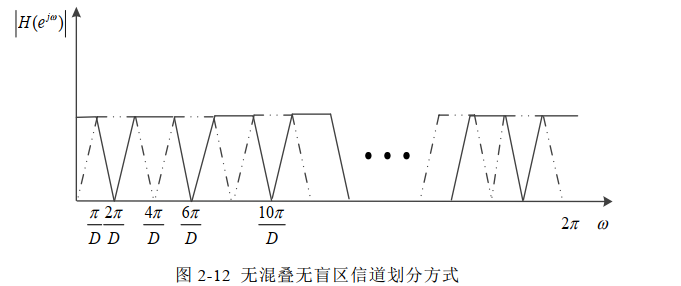
    image.png
    疑问3：为什么上述方法可以避免呢？