Nyquist采样定理

1.低通信号奈奎斯特采样
定义：对于一个频带有限的连续信号f（t），其频谱范围为-wm~+wm，以Ts为时间间隔进行采样得到时域离散值 f（nTs）。时域的离散导致频域发生频谱搬移、周期延拓得到离散信号的频谱Fs（w）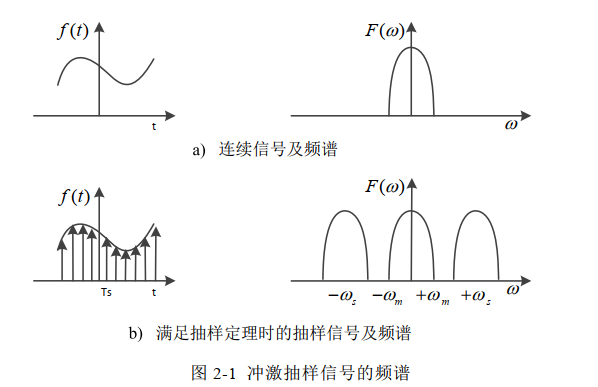

很明显Fs（w）是F（w）以fs（1/Ts）为周期搬移得来的周期函数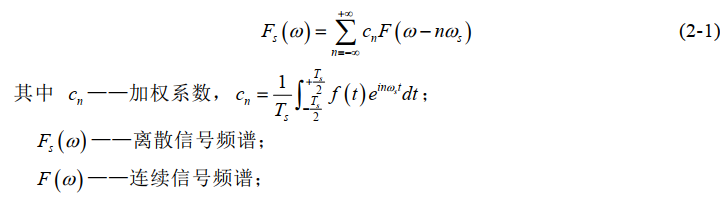 为了防止F（w）搬移时发生频谱混叠，也为了之后能够无误差的恢复得到连续信号，要求fs≥2wm。
意义：既然满足奈奎斯特定律的Fs（w）可以无误差的恢复连续信号f（t），那也就说
明我们可以靠f（t）的几个采样点f（nTs）来代替f（t），没必要分析f（t）的全部数值，为模拟信号的数字化处理提供了理论支撑。
缺点：目前常见信号，如雷达信号，都是有载频的中频带通信号，很少在基带上，所以频带范围通常在（fL，fH）之间，fo=0.5（fL+fH）为其载频值，B=fH-fL为其带宽。fo通常是一个很高的频率，所以如果继续按照fs≥2fm采样率采样，则需要fs非常大，这也就对硬件采样电路提出了高要求，实现比较困难。同时，即使采样率达到了要求，但是目前的数字信号处理速度并不高，满足不了直接处理如此高速的采样数据流，还是得需要降速或者缓存。
2.带通信号奈奎斯特采样
提出背景：解决低通采样定律对于B不太大，但是fH、fL比较高的问题。既然B与fH相比不太大，那么我们只需要一个小的采样频率，保证带宽为B的信号频谱来回搬移的时候不混叠即可。
定义1：


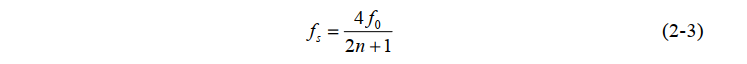
其中，n为fs≥2B的最大正整数。此时fs为一个固定的值。
定义2：

此时fs对应mmax个不同的区间取值。
意义：带通采样定律对采样频率fs的要求大大降低，在fH足够大时，甚至只需要满足fs=2B即可，又因为fs比较小，所以Ts较大，及采集到的f（nTs）数量也会减少，以此减少了离散信号处理的数据量。
局限性：由于回波信号f（t）含有噪声、干扰等一些因素影响，其频谱不可能是很完美的-wm~+wm，所以为了防止频谱混叠发生，还是需要采用更高频率的采样频率。且采样频率越高，总的积分噪声不改变，但是会在更宽的频带上展开，得到更低的基地噪声，有利于后面检测门限的设置。工程当中，要求带通采样所满足的带宽尽可能的大（可以适应不同B的信号），为了降低基地噪声，同时得到更高的信噪比，要求瞬时采样带宽尽可能的宽。通常情况下，对于一个中频信号f（t），采样率一般都较高，即得到的离散化数据f（nTs）较多较快，后续的数字信号处理系统无法直接处理如此快速的数据，因此采完样后，我们需要M倍的整数抽取来降低数据流速度。例如采样频率为fs=100HZ，即1秒采出100个样本点，我们进行5倍抽取，即只处理其中20个样本点，这样对于数字信号处理器来说数据流速度为20HZ，但是要求20HZ≥2B。