Mxnet (46): 使用分解机(Factorization Machines)处理广告推荐

互动数据是用户偏好和兴趣的最基本指示。它在以前介绍的模型中起着至关重要的作用。但是，交互数据通常非常稀疏，有时可能会有很多噪点。为了解决此问题，我们可以将辅助信息（例如项的功能，用户的个人资料，甚至是在发生交互的情况下）整合到推荐模型中。利用这些功能有助于做出建议，因为这些功能可以有效地预测用户的兴趣，尤其是在缺少交互数据时。 因此，推荐模型还必须具有处理这些功能并赋予模型一些内容/上下文意识的能力。有针对性的广告服务已经引起了广泛的关注，并且通常被构造为推荐引擎。推荐符合用户个人品味和兴趣的广告对于提高点击率非常重要。

数字营销人员使用在线广告向客户显示广告。点击率是一种度量广告客户的广告获得的点击次数/展示次数的指标，它表示为使用以下公式计算得出的百分比：

点击率是指示预测算法有效性的重要指标。 点击率预测是一项预测网站上某些内容将被点击的可能性的任务。CTR预测模型不仅可以用于目标广告系统，还可以用于一般项目（例如电影，新闻，产品）推荐系统，电子邮件活动，甚至搜索引擎。它也与用户满意度，转换率密切相关，并且有助于设置广告系列目标，因为它可以帮助广告商设置切合实际的期望。

from collections import defaultdict
from d2l import mxnet as d2l
from mxnet import gluon, np,npx,init,autograd
from mxnet.gluon import nn
from plotly import graph_objs as go
import pandas as pd
import sys
import os
npx.set_np()

1. 获取广告数据集

随着Internet和移动技术的巨大进步，在线广告已成为重要的收入资源，并在Internet行业中产生了绝大部分的收入。展示相关广告或激起用户兴趣的广告很重要，这样临时访客便可以转换为付费客户。我们介绍的数据集是一个在线广告数据集。它由34个字段组成，第一列代表目标变量，该目标变量指示是否单击广告1点击，0未点击。其他列都是用于分类的特征。这些列可能代表广告ID，站点或应用程序ID，设备ID，时间，用户配置文件等。由于匿名和隐私问题，未公开功能的真实语义。

d2l.DATA_HUB['ctr'] = (d2l.DATA_URL + 'ctr.zip','e18327c48c8e8e5c23da714dd614e390d369843f')
data_dir = d2l.download_extract('ctr')

1.1 数据包装器

为了方便数据加载，我们实现了CTRDataset从CSV文件加载广告数据集的，可用于 DataLoader。

class CTRDataset(gluon.data.Dataset):
    def __init__(self, data_path, feat_mapper=None, defaults=None,
                 min_threshold=4, num_feat=34):
        df = pd.read_csv(data_path, sep='\t', header=None)
        df.dropna(inplace=True)
        self.NUM_FEATS, self.count = num_feat, len(df)
        self.data = {i: {'y':[np.float32(row[0])], 'x':row[1:].astype("int64").tolist()} for i, row in enumerate(df.values)}
        self.feat_mapper, self.defaults = feat_mapper, defaults
        self.field_dims = np.zeros(self.NUM_FEATS, dtype=np.int64)
        if self.feat_mapper is None and self.defaults is None:
            self.feat_mapper,  self.defaults = {}, {}
            for i in range(1, self.NUM_FEATS+1):
                feat_count = df[i].value_counts()
                feats = feat_count[df[i].value_counts() >= min_threshold].index
                self.feat_mapper[i] = {feat:i for i, feat in enumerate(feats)}
                self.defaults[i] = len(feats)
        for i, fm in self.feat_mapper.items():
            self.field_dims[i - 1] = len(fm) + 1
        # np.cumsum 函数为累加，作用是保证输出数据根据index分区
        self.offsets = np.array((0, *np.cumsum(self.field_dims).asnumpy()[:-1]))
    def __len__(self):
        return self.count
    def __getitem__(self, idx):
        feat = np.array([self.feat_mapper[i + 1].get(v, self.defaults[i + 1])
                         for i, v in enumerate(self.data[idx]['x'])])
        return feat + self.offsets, self.data[idx]['y']
train_data = CTRDataset(os.path.join(data_dir, 'train.csv'))
train_data[0]

2. 分解机

分解机（FM）是一种可用于分类，回归和排序任务的监督算法。用于是线性回归模型和矩阵分解模型的扩展。此外，它让人联想到带有多项式内核的支持向量机。在线性回归和矩阵分解上，分解机的优势在于：

1. 可以同于 -way 变量交互的模型，这里的 是多项式的阶数通常设置为2。
2. 与分解机关联的快速优化算法可以将多项式计算时间减少到线性复杂度，尤其对于高维稀疏输入而言，效率非常高。

由于这些原因，分解器被广泛用于现代广告和产品推荐中。技术细节和实施方式描述如下。

2.1 2-way 分解机

让 表示一个样本的特征向量，并且 代表对应标签，他可以是实际值的标签也可以是分类标签，比如二分类 “点击/未点击”。二级分解器的模型定义为：

%20%3D%20%5Cmathbf%7Bw%7D0%20%2B%20%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bw%7Di%20x_i%20%2B%20%5Csum%7Bi%3D1%7D%5Ed%5Csum%7Bj%3Di%2B1%7D%5Ed%20%5Clangle%5Cmathbf%7Bv%7D_i%2C%20%5Cmathbf%7Bv%7D_j%5Crangle%20x_i%20x_j%0A#card=math&code=%5Chat%7By%7D%28x%29%20%3D%20%5Cmathbf%7Bw%7D_0%20%2B%20%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bw%7Di%20x_i%20%2B%20%5Csum%7Bi%3D1%7D%5Ed%5Csum_%7Bj%3Di%2B1%7D%5Ed%20%5Clangle%5Cmathbf%7Bv%7D_i%2C%20%5Cmathbf%7Bv%7D_j%5Crangle%20x_i%20x_j%0A)

是全局偏差； 表示第 i个值的权重； 表示特征嵌入; 表示的第 行 ; 是潜在因子的维数; 是两个向量的点积。 模拟 和 特征之间的互动。 一些功能交互很容易理解，因此可以由专家进行设计。但是，大多数其他功能交互都隐藏在数据中，难以识别。因此，自动对要素交互进行建模可以大大减少要素工程的工作量。显然，前两项对应于线性回归模型，而后一项是矩阵分解模型的扩展。如果特征代表项目以及特征 代表用户，第三项正好是用户和项目嵌入之间的点积。值得注意的是 FM 可以推广到更高阶 (degree > 2)。 但是，数值稳定性可能会削弱泛化性。

2.2 高效的优化

用直接方法优化因式分解机会导致复杂度#card=math&code=%5Cmathcal%7BO%7D%28kd%5E2%29) 因为所有成对的交互都需要计算。 T为了解决这个效率低下的问题，我们可以重新组织FM的第三项，这可以大大降低计算成本，从而获得线性时间复杂度（ (#card=math&code=%5Cmathcal%7BO%7D%28kd%29)). 成对交互项的新格式如下：

%5C%5C%0A%20%26%3D%20%20%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bl%3D1%7D%5Ek%20%5Cbig%20((%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%20x_i)%20(%5Csum%7Bj%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bj%2C%20l%7Dx_j)%20-%20%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%5E2%20x_i%5E2%20%5Cbig%20)%20%5C%5C%0A%20%26%3D%20%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bl%3D1%7D%5Ek%20%5Cbig%20((%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%20xi)%5E2%20-%20%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%5E2%20x_i%5E2)%0A%20%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26%5Csum%7Bi%3D1%7D%5Ed%20%5Csum%7Bj%3Di%2B1%7D%5Ed%20%5Clangle%5Cmathbf%7Bv%7D_i%2C%20%5Cmathbf%7Bv%7D_j%5Crangle%20x_i%20x_j%20%5C%5C%0A%20%26%3D%20%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bi%3D1%7D%5Ed%20%5Csum%7Bj%3D1%7D%5Ed%5Clangle%5Cmathbf%7Bv%7D_i%2C%20%5Cmathbf%7Bv%7D_j%5Crangle%20x_i%20x_j%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csum%7Bi%3D1%7D%5Ed%20%5Clangle%5Cmathbf%7Bv%7Di%2C%20%5Cmathbf%7Bv%7D_i%5Crangle%20x_i%20x_i%20%5C%5C%0A%20%26%3D%20%5Cfrac%7B1%7D%7B2%7D%20%5Cbig%20%28%5Csum%7Bi%3D1%7D%5Ed%20%5Csum%7Bj%3D1%7D%5Ed%20%5Csum%7Bl%3D1%7D%5Ek%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%20%5Cmathbf%7Bv%7D%7Bj%2C%20l%7D%20xi%20x_j%20-%20%5Csum%7Bi%3D1%7D%5Ed%20%5Csum%7Bl%3D1%7D%5Ek%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%20x_i%20x_i%20%5Cbig%29%5C%5C%0A%20%26%3D%20%20%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bl%3D1%7D%5Ek%20%5Cbig%20%28%28%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%20xi%29%20%28%5Csum%7Bj%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bj%2C%20l%7Dx_j%29%20-%20%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%5E2%20x_i%5E2%20%5Cbig%20%29%20%5C%5C%0A%20%26%3D%20%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bl%3D1%7D%5Ek%20%5Cbig%20%28%28%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D%7Bi%2C%20l%7D%20xi%29%5E2%20-%20%5Csum%7Bi%3D1%7D%5Ed%20%5Cmathbf%7Bv%7D_%7Bi%2C%20l%7D%5E2%20x_i%5E2%29%0A%20%5Cend%7Baligned%7D%0A)

通过这种重新设计，模型的复杂度大大降低了。此外，对于稀疏特征，仅需要计算非零元素，以使总体复杂度与非零特征的数量呈线性关系。

要学习FM模型，我们可以将MSE损失用于回归任务，将交叉熵损失用于分类任务，将BPR损失用于排名任务。标准优化器（例如SGD和Adam）可以进行优化。

3. 模型实现

以下代码实现了分解机。很明显，FM由线性回归块和有效特征交互块组成。由于将CTR预测视为分类任务，因此我们在最终得分上应用了S形函数。

class FM(nn.Block):
    def __init__(self, field_dims, num_factors):
        super(FM, self).__init__()
        num_inputs = int(sum(field_dims))
        self.embedding = nn.Embedding(num_inputs, num_factors)
        self.fc = nn.Embedding(num_inputs, 1)
        self.linear_layer = nn.Dense(1, use_bias=True)
    def forward(self, x):
        square_of_sum = np.sum(self.embedding(x), axis=1) ** 2
        sum_of_square = np.sum(self.embedding(x) ** 2, axis=1)
        x = self.linear_layer(self.fc(x).sum(1)) \
            + 0.5 * (square_of_sum - sum_of_square).sum(1, keepdims=True)
        x = npx.sigmoid(x)
        return x

4. 加载数据集

我们使用上一部分的CTR数据包装器加载在线广告数据集。

batch_size = 2048
data_dir = d2l.download_extract('ctr')
train_data = d2l.CTRDataset(os.path.join(data_dir, 'train.csv'))
test_data = d2l.CTRDataset(os.path.join(data_dir, 'test.csv'),
                           feat_mapper=train_data.feat_mapper,
                           defaults=train_data.defaults)
train_iter = gluon.data.DataLoader(
    train_data, shuffle=True, last_batch='rollover', batch_size=batch_size,
    num_workers=d2l.get_dataloader_workers())
test_iter = gluon.data.DataLoader(
    test_data, shuffle=False, last_batch='rollover', batch_size=batch_size,
    num_workers=d2l.get_dataloader_workers())

5. 训练模型

使用处理计算机视觉时使用的训练函数：

def accuracy(y_hat, y): 
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.astype(y.dtype) == y
    return float(cmp.sum())
def train_batch(net, features, labels, loss, trainer, devices, split_f=d2l.split_batch):
    X_shards, y_shards = split_f(features, labels, devices)
    with autograd.record():
        pred_shards = [net(X_shard) for X_shard in X_shards]
        ls = [loss(pred_shard, y_shard) for pred_shard, y_shard
              in zip(pred_shards, y_shards)]
    for l in ls:
        l.backward()
    # ignore_stale_grad代表可以使用就得梯度参数
    trainer.step(labels.shape[0], ignore_stale_grad=True)
    train_loss_sum = sum([float(l.sum()) for l in ls])
    train_acc_sum = sum(accuracy(pred_shard, y_shard)
                        for pred_shard, y_shard in zip(pred_shards, y_shards))
    return train_loss_sum, train_acc_sum
def train(net, train_iter, test_iter, loss, trainer, num_epochs,
               devices=d2l.try_all_gpus(), split_f=d2l.split_batch):
    num_batches, timer = len(train_iter), d2l.Timer()
    epochs_lst, loss_lst, train_acc_lst, test_acc_lst = [],[],[],[]
    for epoch in range(num_epochs):
        metric = d2l.Accumulator(4)
        for i, (features, labels) in enumerate(train_iter):
            timer.start()
            l, acc = train_batch(
                net, features, labels, loss, trainer, devices, split_f)
            metric.add(l, acc, labels.shape[0], labels.size)
            timer.stop()
            if (i + 1) % (num_batches // 5) == 0:
                epochs_lst.append(epoch + i / num_batches)
                loss_lst.append(metric[0] / metric[2])
                train_acc_lst.append(metric[1] / metric[3])
        test_acc_lst.append(d2l.evaluate_accuracy_gpus(net, test_iter, split_f))
        if((epoch+1)%5==0):
            print(f"[epock {epoch+1}] train loss: {metric[0] / metric[2]:.3f}  train acc: {metric[1] / metric[3]:.3f}", 
                      f"  test_loss: {test_acc_lst[-1]:.3f}")
    print(f'loss {metric[0] / metric[2]:.3f}, train acc '
          f'{metric[1] / metric[3]:.3f}, test acc {test_acc_lst[-1]:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec on '
          f'{str(devices)}')
    fig = go.Figure()
    fig.add_trace(go.Scatter(x=epochs_lst, y=loss_lst, name='train loss'))
    fig.add_trace(go.Scatter(x=epochs_lst, y=train_acc_lst, name='train acc'))
    fig.add_trace(go.Scatter(x=list(range(1,len(test_acc_lst)+1)), y=test_acc_lst, name='test acc'))
    fig.update_layout(width=580, height=400, xaxis_title='epoch', yaxis_range=[0, 1])
    fig.show()
def train_fine_tuning(net, learning_rate, batch_size=64, num_epochs=5):
    train_iter = gluon.data.DataLoader(train_imgs.transform_first(train_augs), batch_size, shuffle=True)
    test_iter = gluon.data.DataLoader(test_imgs.transform_first(test_augs), batch_size)
    net.collect_params().reset_ctx(npx.gpu())
    net.hybridize()
    loss = gluon.loss.SoftmaxCrossEntropyLoss()
    trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': learning_rate, 'wd': 0.001})
    train(net, train_iter, test_iter, loss, trainer, num_epochs, [npx.gpu()])

默认情况下，学习率设置为0.01，嵌入大小设置为20。使用Adam优化和 SigmoidBinaryCrossEntropyLoss损失函数

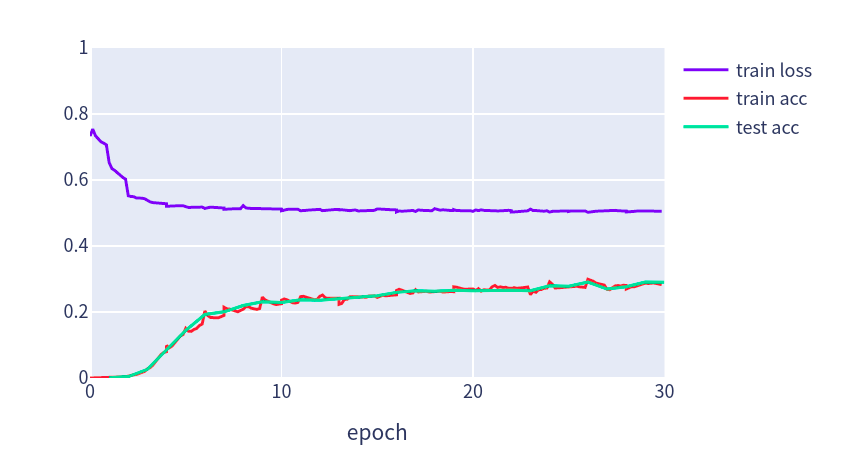
devices = d2l.try_all_gpus()
net = FM(train_data.field_dims, num_factors=20)
net.initialize(init.Xavier(), ctx=devices)
lr, num_epochs, optimizer = 0.02, 30, 'adam'
trainer = gluon.Trainer(net.collect_params(), optimizer, {'learning_rate': lr})
loss = gluon.loss.SigmoidBinaryCrossEntropyLoss()
train(net, train_iter, test_iter, loss, trainer, num_epochs, devices)

6. 参考

https://d2l.ai/chapter_recommender-systems/fm.html

7.代码

github