概念

在统计学中，回归分析（regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照涉及的变量的多少，分为一元回归和多元回归分析；按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

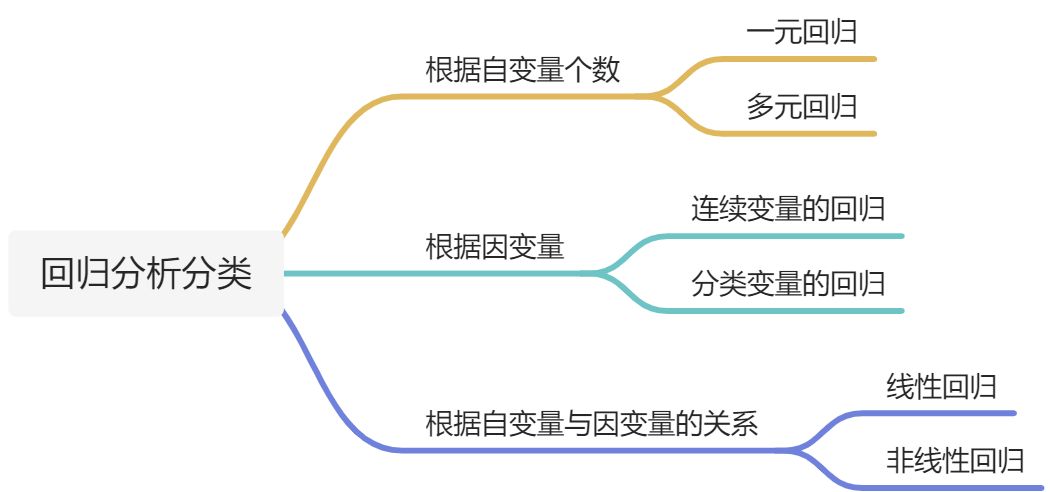
回归分析分类

探查变量之间的数量变化规律，并通过一定的数学表达式来描述这种关系，进而确定一个或几个变量的变化对另一个变量的影响程度。

回归分析是研究变量之间统计关系的方法，侧重考察回归分析的类型。

• 因变量与自变量都是定量变量的回归分析：普通回归分析
• 因变量是定量变量，自变量中有定性变量的回归分析：含有哑变量的回归分析
• 因变量是定性变量的回归分析：Logistic回归分析。

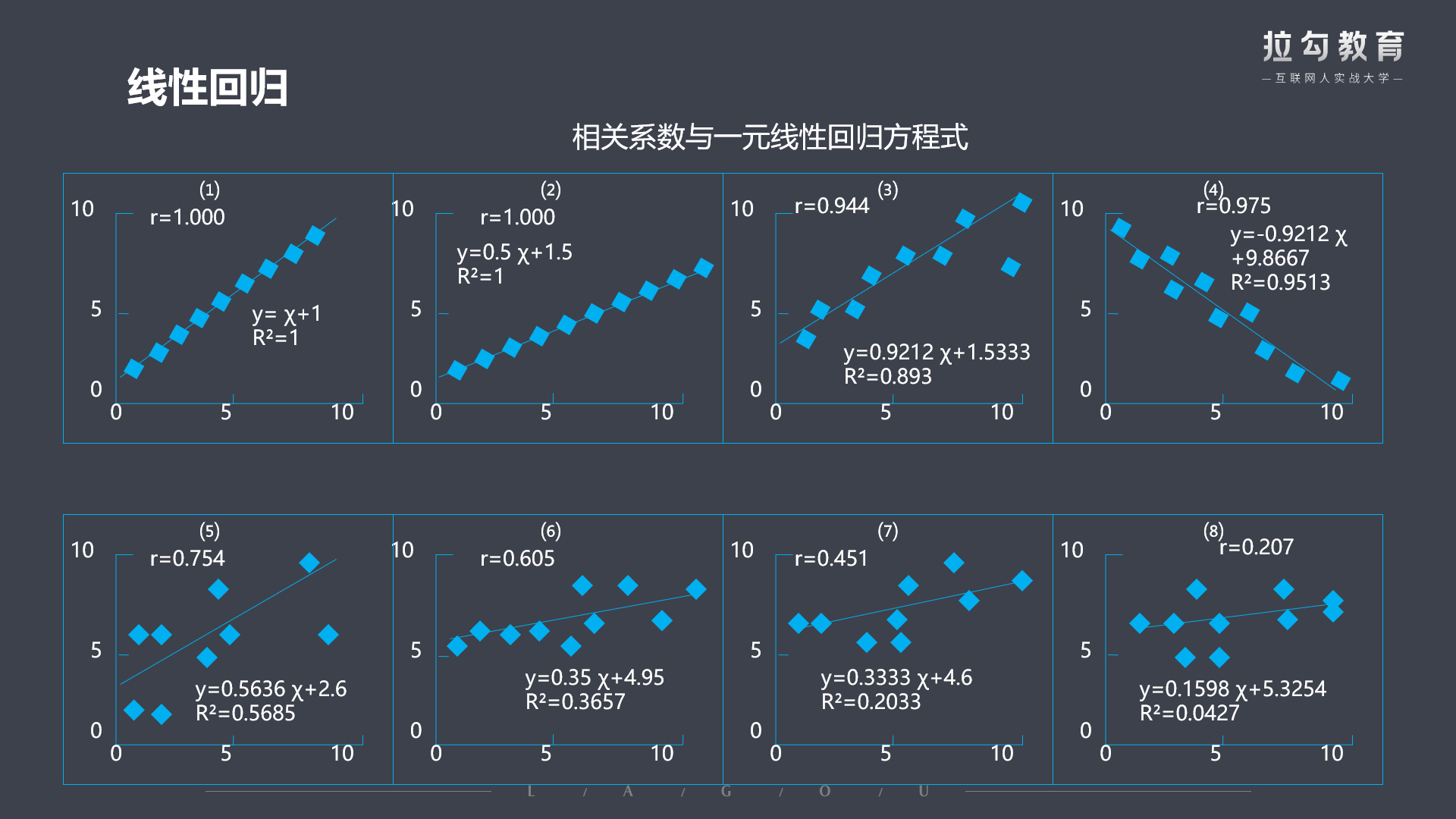
线性回归

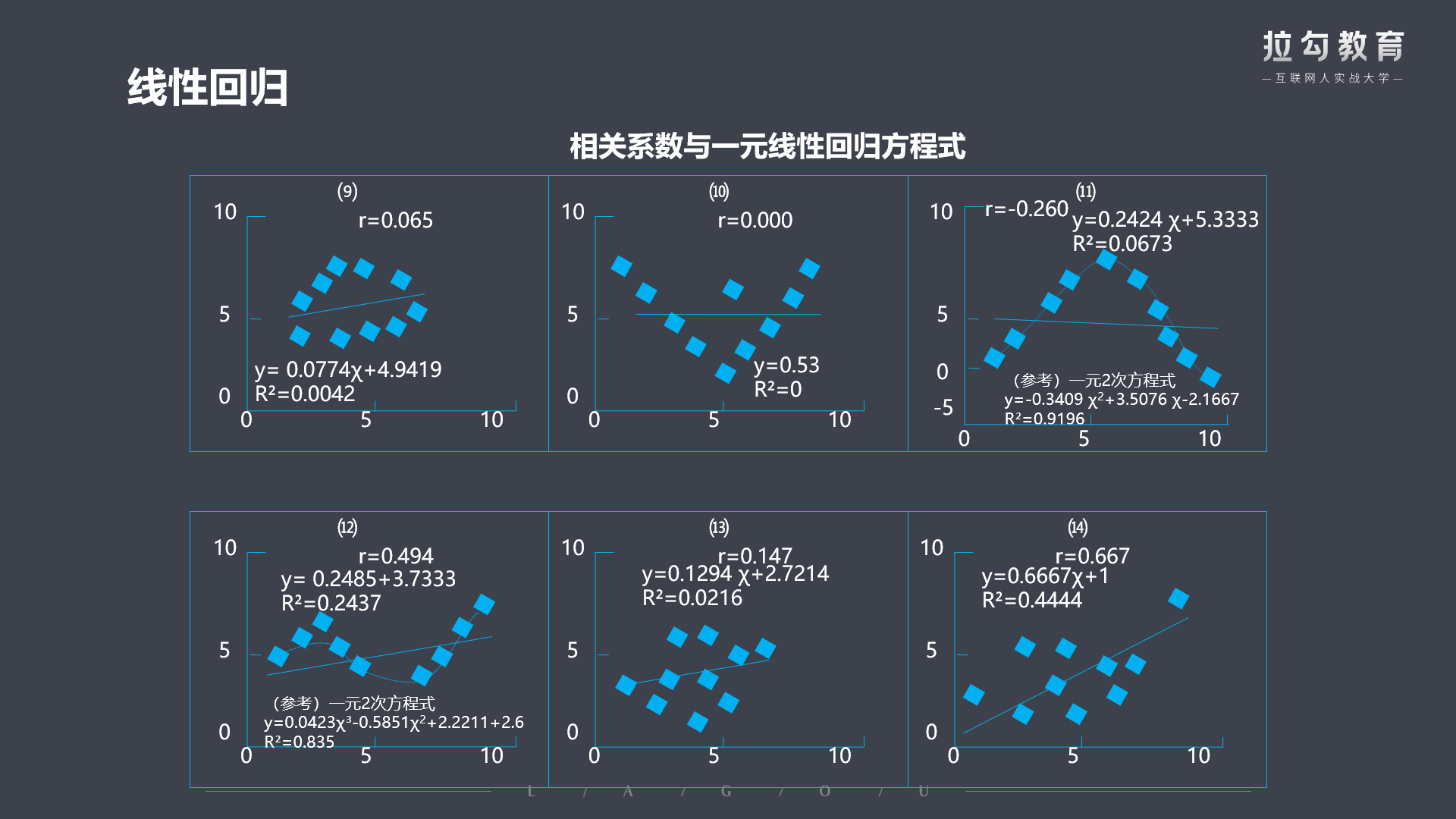
运用场景

目的：当需要用一个数学表达式（模型）表示多个因素（原因）与另外一个因素之间的关系时。

应用：

• 分析哪些自变量对因变量存在显著影响作用。R2 可以不要求大于0.8
• 通过选择对因变量存在显著影响的自变量，建立预测因变量取值的预测模型。R2 必须要求大于0.8

通常情况R2 >0.8就可以用来做预测。

回归分析过程

回归分析前提

因为有了以下几个前提所以回归分析是参数检验。

1. 线性趋势

• 使用散点图判断自变量和因变量之间的线性关系，线性才能使用回归分析。

1. 独立性

• 因变量y的取值相互独立，之间没有联系。
• 反映到模型中要求残差间相互独立，不存在自相关，否则应采用自回归模型分析。

残差：模型预测值与真实值之间的差。

1. 正态性

• 自变量的任何一个线性组合因变量均服从正态分布。
• 反映到模型中要求残差服从正态分布。

1. 方差齐性

• 自变量的任何一个组合因变量的方差均相同。
• 反映到模型中要求残差的方差齐性。

多元线性回归的步骤

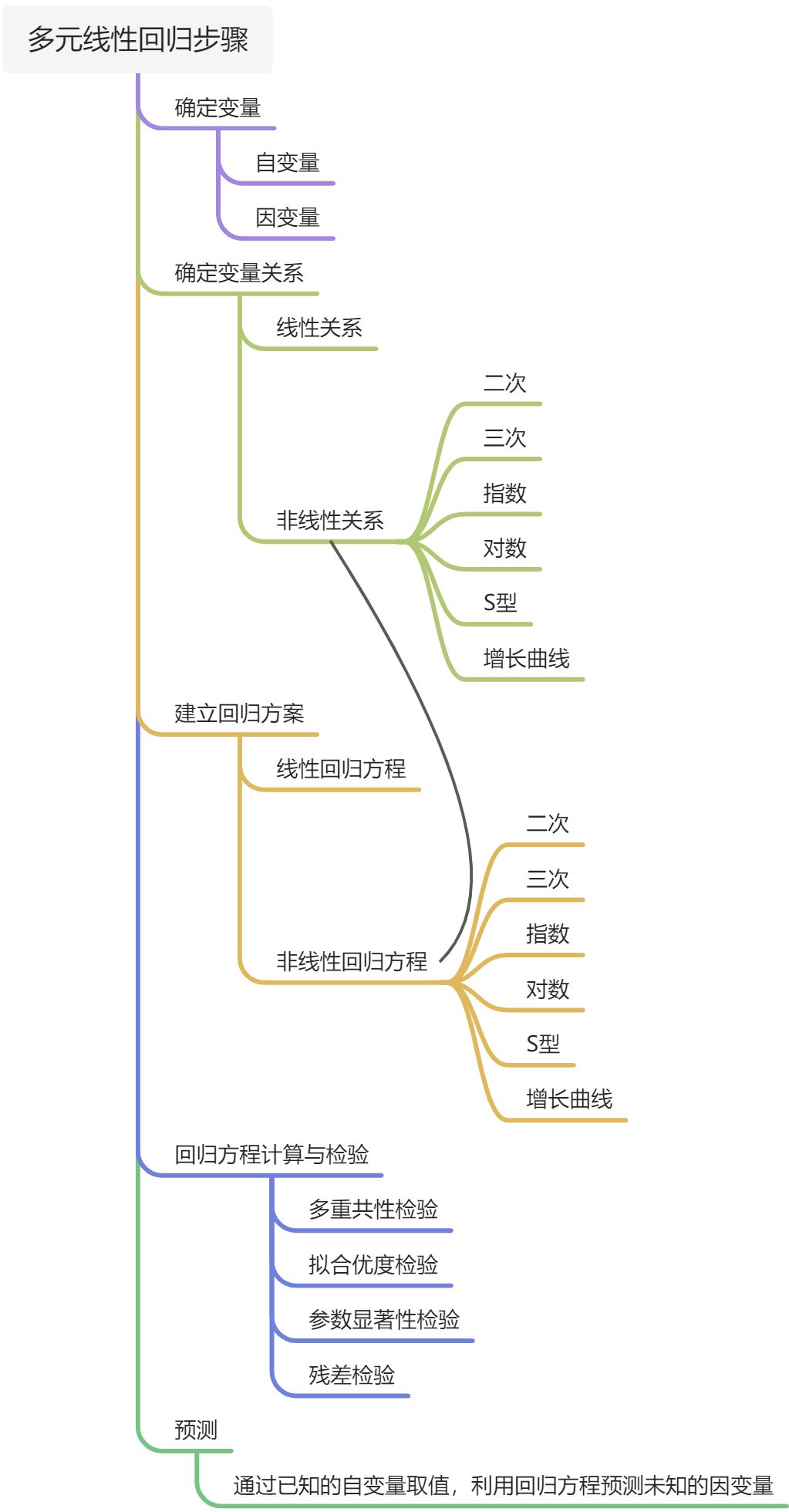
1. 选择变量

• 因变量：根据研究需求或问题推导得出。
• 自变量：前人研究成果；个人经验。

1. 确定自变量与因变量的关系

• 如何确定？
• 依次将自变量和因变量画散点图，看是否是线性关系
• 通过卡方检验，T检验，F检验或相关分析法，分析每个备选的自变量与因变量之间是否存在显著的相关性，将因变量明显没有相关性的自变量剔除，不加入后期的模型中。

1. 选择对应的线性或非线性回归方程，进行各项参数的计算。

2. 对模型进行全方位检验

• 多重共线性检验（相关分析法、VIF/容忍度）
  • 检验多个自变量之间是否存在相关性较高的变量，如有则保留因变量相关性最高的一个自变量
• 模型拟合优度检验
• 方差检验：检验自变量与因变量是否存在显著影响关系；
• 判定系数（R方）：0-1之间，越接近1表示自变量对因变量的解释能力越高，模型越好；
• 残差检验：常用的方法包括残差正态性检验、DW检验、异方差检验。
• 自变量参数检验（参数估计方法：普通最小二乘法（OLS：Ordinary Least Square）和极大似然估计（MLE：Maximum Likelihood Estimate））

线性回归

向前筛选（Forward） 是自变量不断进入回归模型的过程。首先，选择与因变量具有最高线性相关系数的自变量进入模型，并进行回归分析的各种检验；然后，在剩余的变量中寻找与自变量偏相关系数最大且通过检验的变量进入模型，并对新建立的模型进行各种检验；这一过程一直重复，直到再也没有可进入模型的变量为止。 向后筛选（Backward） 是自变量不断剔除出回归模型的过程。首先，所有变量全部选入回归模型中，并对回归方程进行各种检验；然后，在回归系数显著性检验不显著的一个或多个变量中，剔除t检验值（或其他检验值）最小的变量，并重新建立回归方程并进行各种检验；如果新建回归模型中所有变量的回归系数检验都显著，则回归方程建立结束。否则按照上述方法再依次剔除最不显著的变量，直到再也没有可剔除的变量为止。 逐步筛选（Stepwise） 是向前筛选和向后筛选的综合。随着变量的不断引入，自变量之间可能存在一定程度的多重共线性，使得某些已经进入模型的自变量不再显著，这样造成最终回归模型可能包含一些不显著的自变量。逐步回归是在向前筛选基础上，结合向后筛选，在每个变量进入模型后再次判断是否存在应该剔除的自变量。

SPSS

解决问题：分析影响人们家庭收入的因素有哪些，建立预测收入的回归模型。

因变量：家庭收入
自变量：年龄、学历、性别、工作年限

虚拟变量

作用

分类变量无法参与到回归模型中的加减乘除运算。

虚拟变量也称哑变量，出现时取“1”，否则取“0”，虽是数值，但是没有数值的实际意义，仅说明性质和属性。

操作

将分类编码统一转换为0/1取值。

转换-重新编码为不同变量，重新定义新值与旧值的关系。

分析-回归-线性；统计-勾选共线性诊断-DW

图-标准化残差图：直方图，正态概率图

结果解读

1. 拟合优度检验

• R²值
• F值：F值对应的概率P值小于0.05，研究假设成立，即至少有一个自变量对因变量存在显著影响。

1. 参数显著性检验

• 根据每个自变量的t值对应的概率P值是否小于0.05，如小于0.05则研究假设成立，即该自变量对因变量存在显著影响。
• 根据下表得出，工作年限和学历对收入存在显著影响，而年龄和性别没有。
• 通过标准化系数来判断两者对影响的程度大小，可知工作年限的影响明显大于学历，工作年限对收入影响程度：在其他变量不变的情况下，工作年限每增加一个单位（年）则因变量家庭收入平均增加6.279个单位；
• 学历对收入的影响程度：ED1 = -51.042表示ed1代表的学历人群（高中以下）比对照的学历人群（大专）在因变量家庭收入上，平均第51,042单位；

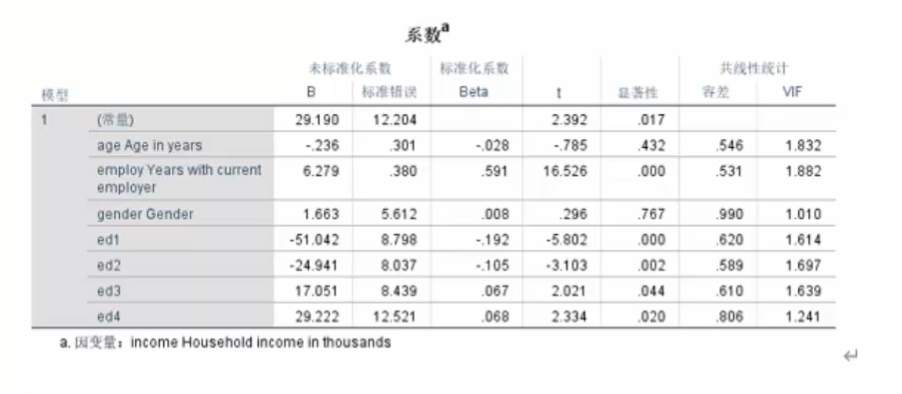
1. 共线性检验

• 通常根据VIF值 >10代表自变量之间存在共线性。

1. 残差检验

• DW=2，表示残差不存在自相关性。

1. 回归方程

• 通过逐步回归法将对因变量没有显著迎新啊的自变量从模型中删除，得到干净的模型。