使用场景

分类问题、二分类、多分类、非参数检验

做分类预测模型，是一个非参数检验方法。可用于 二分类，无序多分类、有序多分类。

操作

分析-回归-二元

结果解读

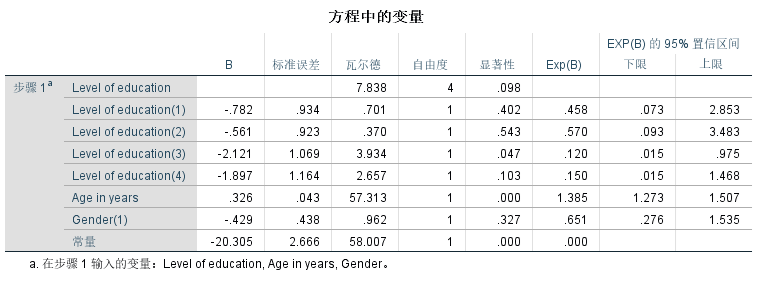
• 根据参数检验中的P<0.05，得到自变量对因变量存在显著影响。
• 根据wald值大小判断自变量对因变量的影响程度差异排名。
• 优势比（OR）值大于1，表示该自变量会增加因变量取1 的概率，反之会降低。
• 连续自变量对因变量的影响程度：在其他变量不变的情况下，当年龄增加一个单位（1岁）时，优势比增加1.385倍（年龄越大退休概率越大）
• 分类自变量对因变量的影响程度：在其他变量不变的情况下，大专学历的优势比是研究生学历优势比的0.120倍（大专学历的退休概率高于研究生学历的概率）

logistic公式

ln (p/1-p)) = 20.305-0.782ed1-0.561ed2-2.121ed3-1.897ed4—0.326age+0.429gender

并非是最终模型，但写模型公式的思路是这样的。

有序多分类

• 首先要进行平行性检验：检验当因变量划分不同取值时建立的多个二元logistic回归，自变量对因变量的影响程度是相同的。如果改检验不成立，则不能选择有序多分类模型，改用无序多分类模型。

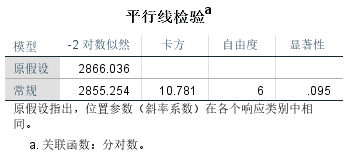
当P>0.05 说明h0成立，则平行性检验成立，可以建立有序分类模型。

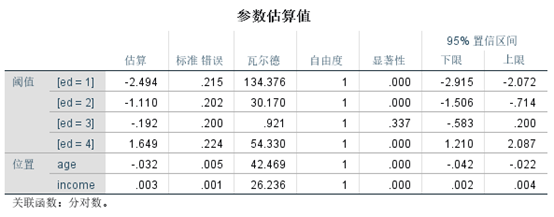
解读：

模型公式

1. ln(p1/(1-p1)) = -2.494-0.032age+0.003income（p1表示学历取1的概率）
2. ln(p1/(1-p2)) = -1.110-0.032age+0.003income（p2表示学历取1、2的概率）
3. ln(p1/(1-p3)) = -0.192-0.032age+0.003income（p3表示学历取1、2、3的概率）
4. ln(p1/(1-p4)) = -1.649-0.032_age+0.003_income（p4表示学历取1、2、3、4的概率）