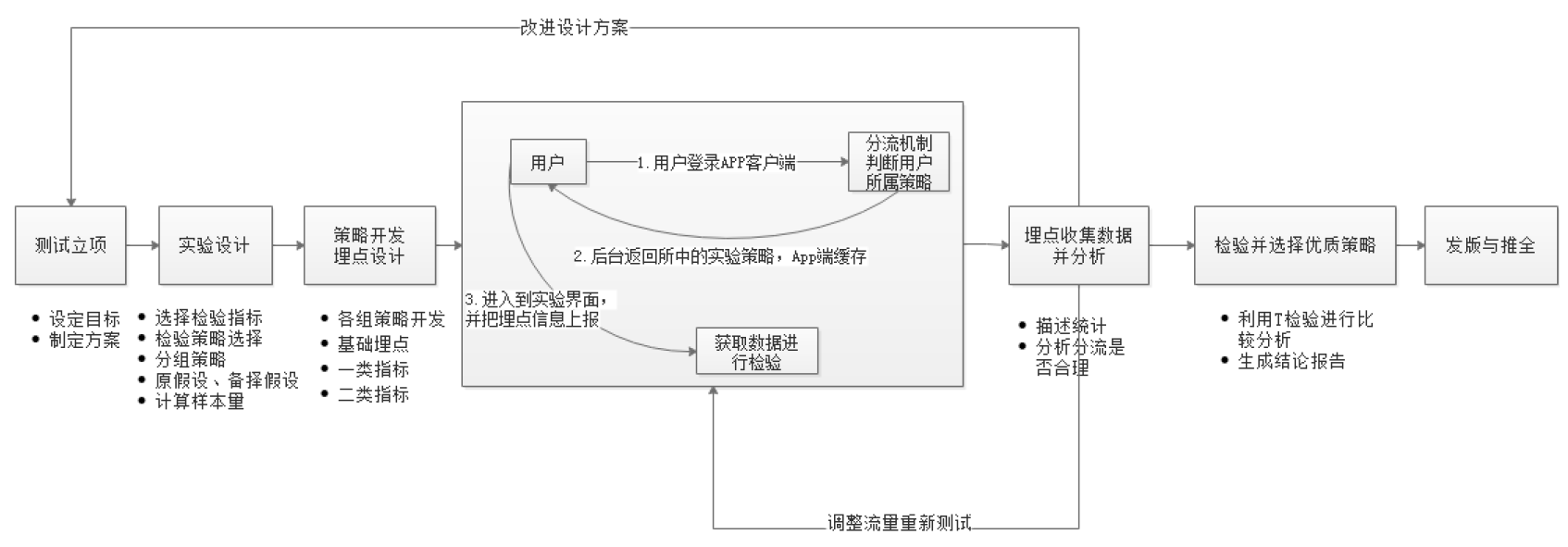
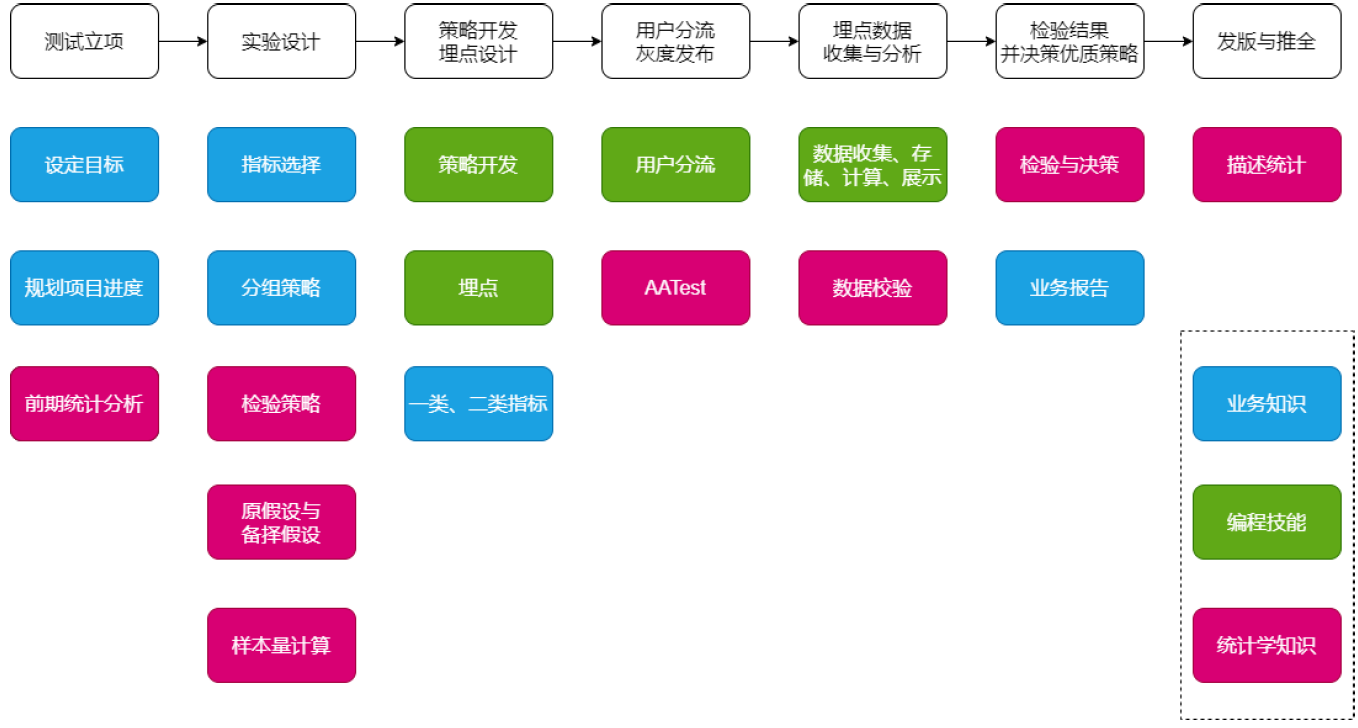
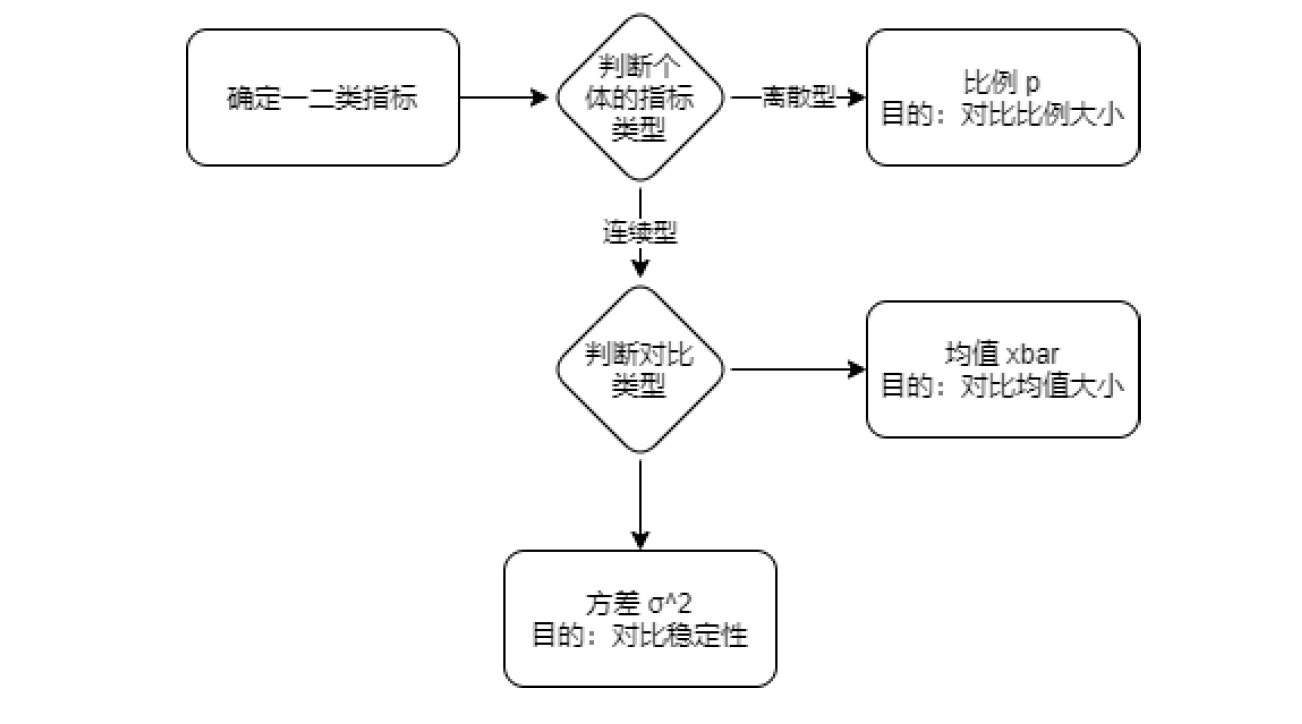
一、认识ABTest

第七阶段 数据分析应用案例ABTest（有板书）v3.pdf

参考文章：AB test详解 | 什么是ABTest | 拉勾ABtest

ABTest，简单来说，就是为同一个产品目标制定两个方案（比如两个页面一个用红色的按钮、另一个用蓝色的按钮），让一部分用户使用A方案，另一部分用户使用B方案，然后通过日志记录用户的使用情况，并通过结构化的日志数据分析相关指标，如点击率、转化率等，从而得出那个方案更符合预期设计目标，并最终将全部流量切换至符合目标的方案。

特点

• 可控性高。数据分流+灰度发布实现了统计学上的抽样+控制变量。
• 数据收集十分全面。多种埋点功能提供了多种实验的可能。
• 高速。大量用户+快速的数据收集存储功能使得企业极大的节省了时间成本。

ABTest的必要性

优点

1. 风险控制：降低开发成本及用户流失风险。
2. 科学择优：用严密的计算逻辑替领导层减少决策成本。

缺点

1. 细小改变与重大改版的博弈：只能做到局部最优，无法做到全局最优。
2. 数据驱动与业务灵感的平衡：数据驱动无法让业务方获得业务灵感，业务灵感需要跳出数据的框架去获得，数据分析师要注意日常工作中有时需跳出数据的桎梏去贴近业务。

   收获

• 能够直接将所学的ABTest内容应用于现有工作场景，提升企业决策科学性；
• 优化现有工作ABTest流程，提升工作表现，提升职位不可替代性；
• 灵活应对面试、笔试提问，轻松通过面试；
• 大厂敲门砖，升职加薪必备良药。

二、学习企业ABTest业务流程

实际企业业务流程

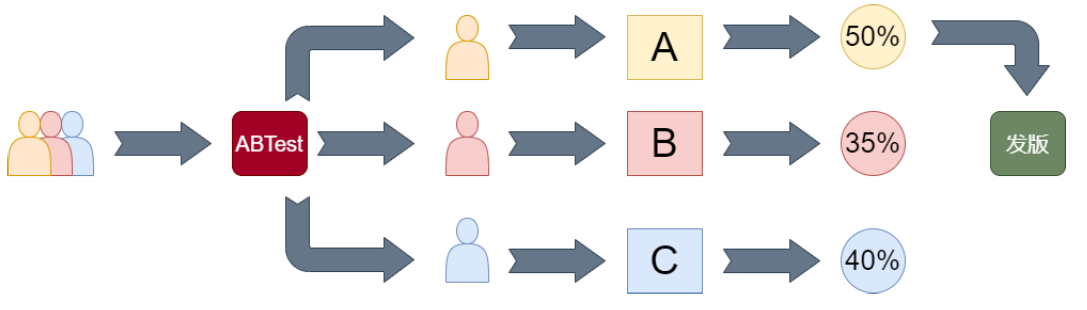
项目流程

假设检验

假设检验是ABtest的基础，理论情况下的假设检验方法和实际业务中的问题有比较大的出入，需要根据实际业务目标来设置H0,H1。

假设检验的逻辑

先说一下假设检验的基本逻辑。 简单说，假设检验的思路是： 通过“小概率事件在少量实验中是几乎不可能出现的”这一结论，去证明假设是错误的，从而反证假设的另一面很可能是正确的。 以投飞镖的例子，如果假设你是“百发百中”，那要把你投的每一次成绩进行统计，并且证明每一次投的都射中靶面了。 这显然操作难度很大，因为如果你投了成千上万次，这是一个极大的工作量。 但如果去证明你不是“百发百中”，就简单多了，只要有一次没上靶的案例，你就不是“百发百中”了。 原假设，也叫零假设，一般用H0来表示，一般是一个正命题，你要做的就是找到一个反例去否定它。 而原假设的反面，叫做备择假设，一般用H0来表示，如果拒绝了原假设，也就证明了备择假设是正确的。— 参考：假设检验的逻辑

普通逻辑

if A then NOT B

简单理解就是如果A事件成立那么B事件就不会成立。

• 如果我有钱A，我肯定不会买安卓手机NOT B
• 如果我有钱A，我肯定不会买十万以下的车NOT B
• 如果我有钱A，我肯定不会当打工人NOT B。

以上案例是假设检验的普通逻辑，普通逻辑不是很严谨，它会有逆反命题，也就是反推过来会导致A事件不成立。

• 买了安卓手机，我就肯定没有钱
• 买了十万以下的车，我就肯定没有钱

• 当打工人，我就肯定没有钱

  
  先决条件把握度不高的话就会严重影响B出现后我们对NOT A 的 推断。由此引出假设检验的逻辑。

假设检验逻辑

if A then probably β NOT B;

这个时候，如果我们知道同条件下的各β，我们就能判断各先决条件的可信度。同理，我们也可以有逆反命题：

• 如果我有钱A1，我就大概率β1 不会买安卓手机NOT B
• 如果我有钱A2，我就大概率β2 不会买十万以下的车NOT B
• 如果我有钱A3，我就大概率β3 不会当打工人NOT B

逆反命题

• 当我买了安卓手机B1，我就大概率β1推断没有钱NOT A
• 当我买了十万以下的车B2，我就大概率β2推断没有钱NOT A
• 当我当打工人B3，我就大概率β3推断没有钱NOT A

总结：通过对我的长期观察，发现β3>β2>β1

β在这里就是一个可信度，有它在会大大加强对NOT B 的推断。

由此可推断出假设检验的基本逻辑：当你想证明一个事件 A 不成立的时候。你可以先找到一件当事件 A 成立时很大程度不会发生的事件 B。这时当你发现事件 B 发生的时候，你就有很大把握证明A不成立。所以我们只需要证明“事件 A 成立时很大程度不会发生的事件 B”，我们就能让以上的逻辑成立。

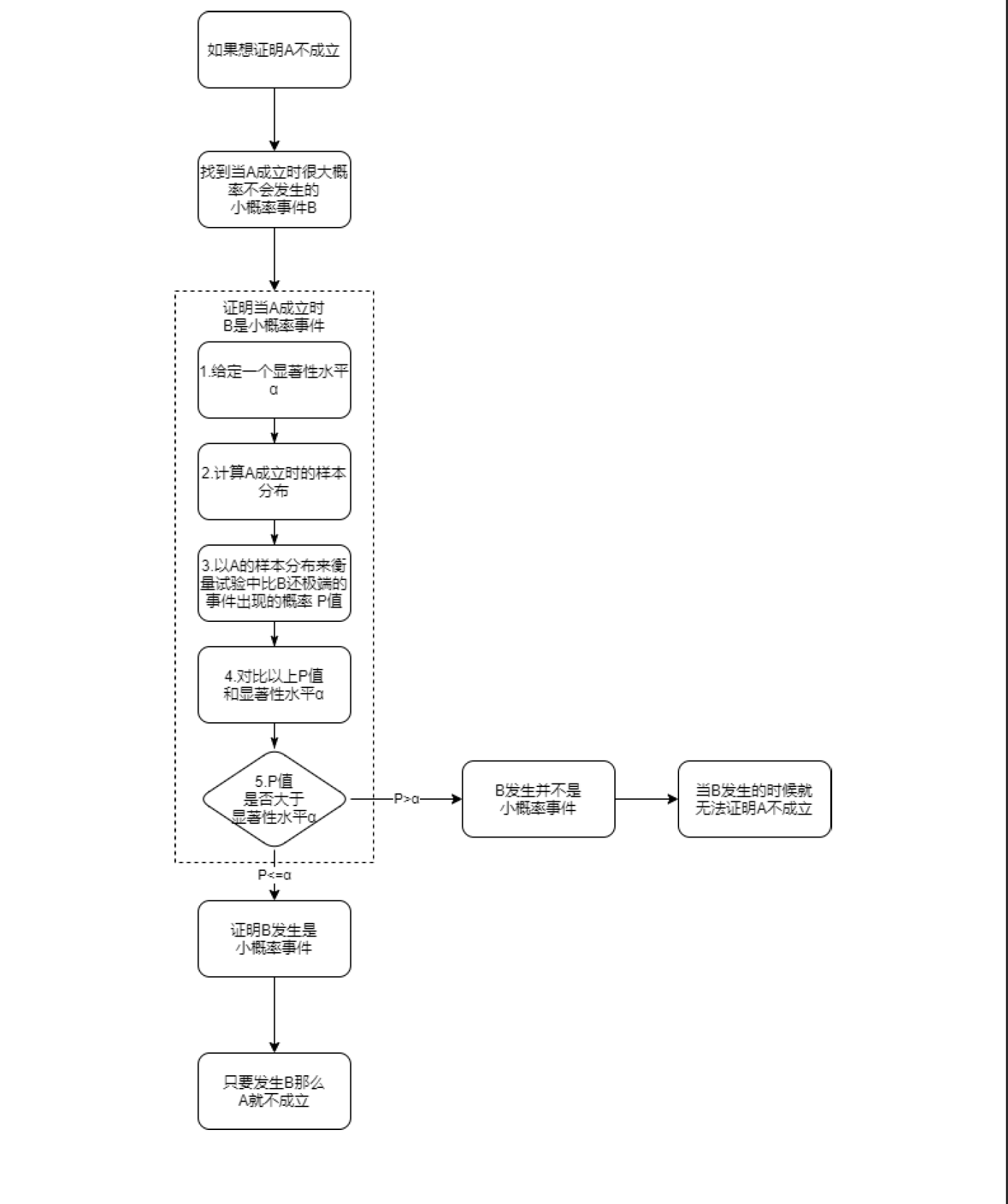
假设检验关键步骤

【补充】
【补充】ABTest八大问 | 假设检验 | AB试验的统计学原理

• 一组完全对立的假设
  • H0: A事件成立 A
  • H1: A事件不成立 NOT A
• 我们主要做的事情：是通过证明B在A条件的前提下是一个小概率事件，只要出现了事件B，就能证明事件A不成立，选择拒绝原假设。
• 需要一个小概率发生的极端事件B

• 给定一个“大概率”阈值

  • 也就是犯一类错误的概率
  • 通常设置为0.05
  • 也叫显著性水平，犯一类错误的后果越严重，显著性水平就需要越低

• 计算A成立时的分布和样本统计量分布

二项分布：只出现两种结果的n次独立试验的分布。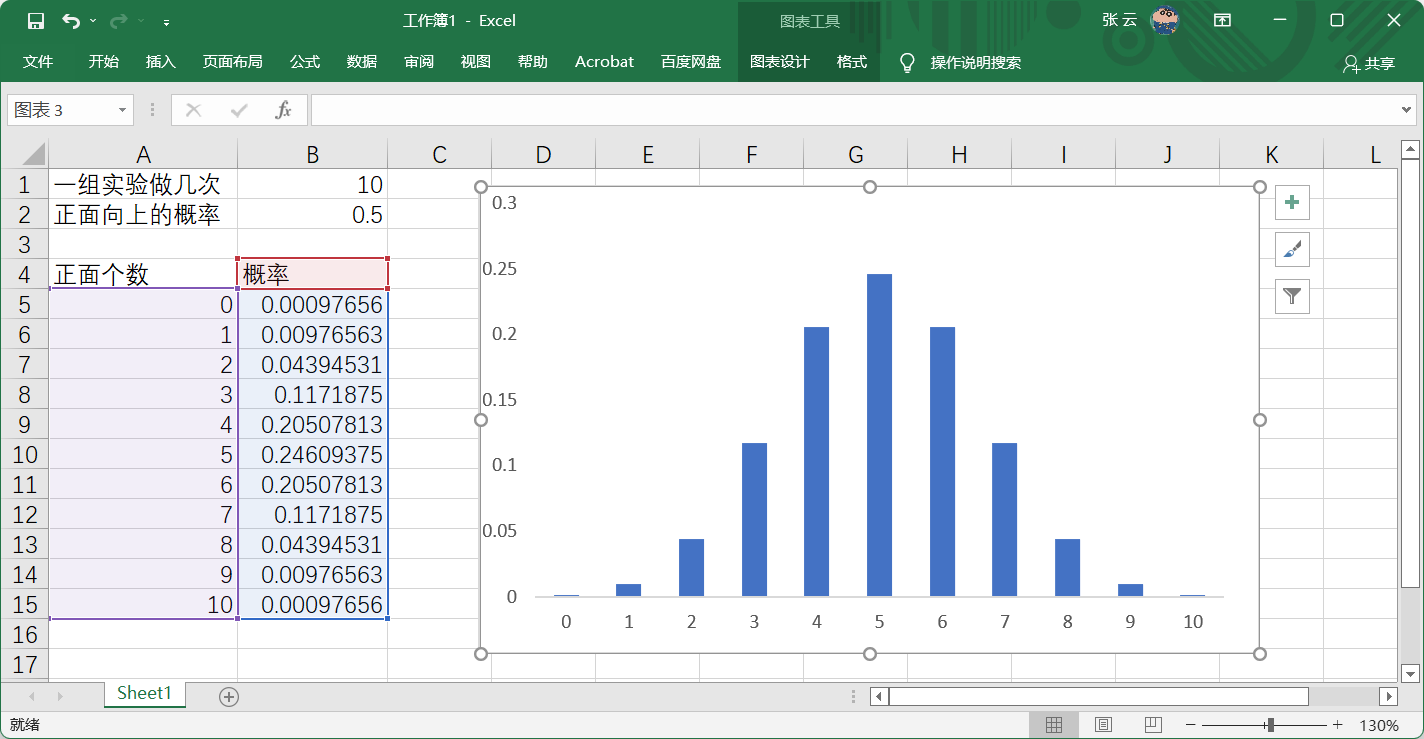

这个分布就是样本分布。

• 对比B发生时的统计量位置，计算更极端事件的发生概率 P值
• 对比P值和显著性水平的大小，证明在A事件发生的条件下，B事件是小概率事件

拒绝域

拒绝域亦称否定域，又称临界域，是统计学的基本概念之一。能够拒绝原假设的检验统计量的所有可能取值的集合，称为拒绝域；不能够拒绝原假设的检验统计量的所有可能取值的集合称为接受域；根据给定的显著性水平确定的拒绝域的边界值，称为临界值。拒绝域就是由显著性水平α所围成的区域。如果利用样本观测结果计算出来的检验统计量的具体数值落在了拒绝域内，就拒绝原假设，否则就不能拒绝原假设。

拒绝域的大小与人们事先选定的显著性水平α有一定关系。在确定了显著性水平 α之后，就可以根据 α 值的大小确定出拒绝域的具体边界值。

在给定显著性水平α后，查统计表就可以得到具体的临界值（也可以直接由Excel中的函数命令计算得到）。将检验统计量的值与临界值进行比较，就可做出拒绝或不拒绝原假设的决策。

当样本量固定时，拒绝域的面积随着α的减小而减小。α值越小，为拒绝原假设所需要的检验统计量的临界值与原假设的参数值就越远。拒绝域的位置取决于检验是单侧检验还是双侧检验。双侧检验的拒绝域在抽样分布的两侧。而单侧检验中，如果备择假设具有符号“<”，拒绝域位于抽样分布的左侧，称为左侧检验；如果备择假设具有符号“>”，拒绝域位于抽样分布的右侧，称为右侧检验。

• 如何判断一个样本统计量符合什么分布

样本统计量：样本中对于样本个体的统计函数结果；取均值、计算比例、求方差；比如每个样本个体能产生多少个值，求平均最大值。

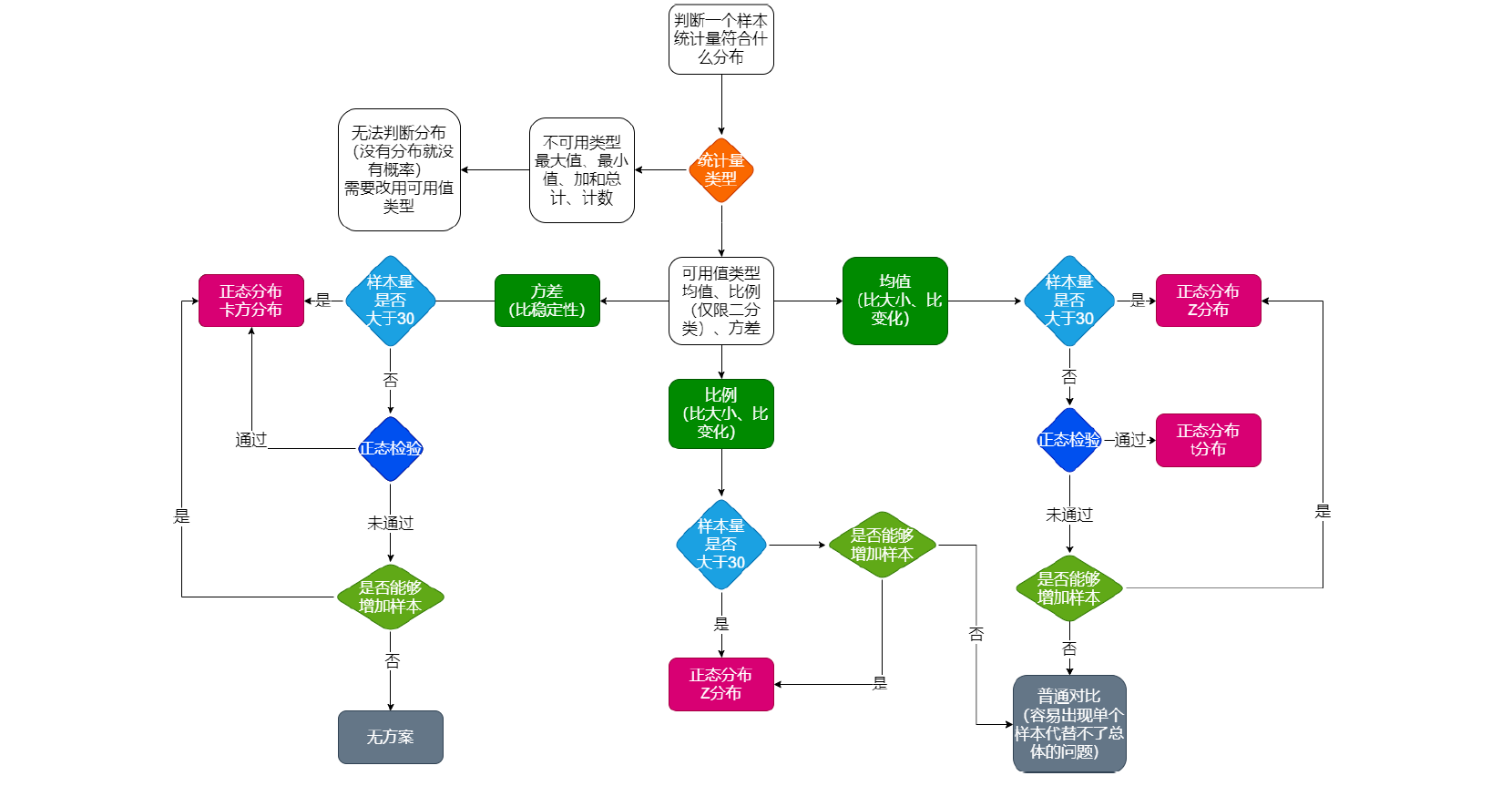
统计分布

参考：常见的统计分布

多个总体问题

三、企业AB试验关键流程

整体实验设计与分析流程

确定业务目标

一般来说确定试验目标就是要对什么目标做改进，互联网企业中一般是产品变动或者策略变动。

1. 明确要提升的业务目标
   1. 如果明确这个部分，实验会显得比较精简，目标明确。
2. 明确要改进的产品/策略

选择检验指标

• 一类指标：不呢容忍变差的指标
  • 需要给一类指标设定一个阈值，下降到多少的时候是“不能忍受”
• 二类指标：目标提升的指标

场景举例：

选择统计量

确定H0与H1

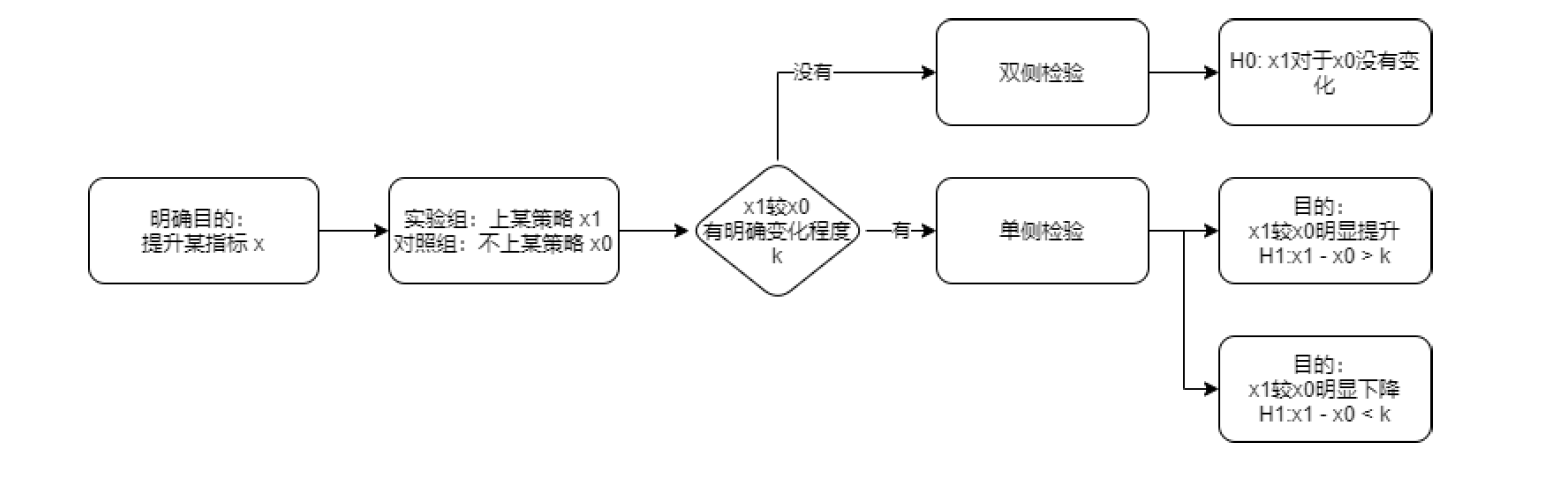
• 明确目的：提升目标指标
• 设定实验组和对照组
  • 实验组X1使用策略A
  • 对照组X0不使用策略A

定目标的时候，除了定目标、方向之外，还要定优化程度。

• 双侧检验
  • 证明实验组H0对于对照组H1有没有变化。证明了变化后，直接用统计量对比是正向变化还是负向变化
• 单侧检验

两类错误的防范

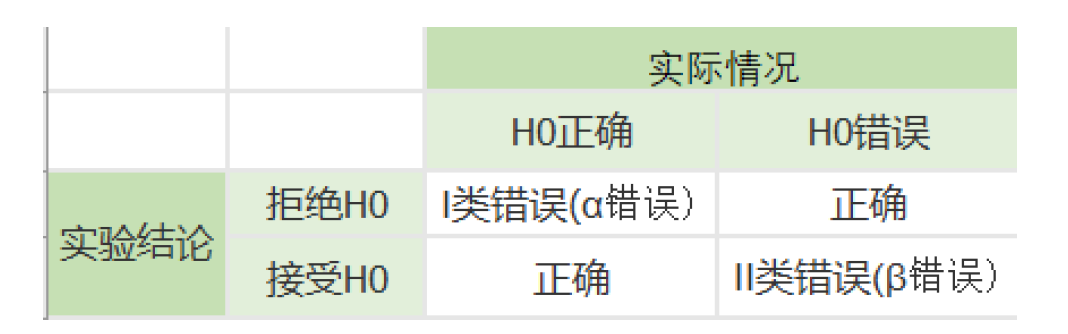
1、 α+β不一定等于1。
2、在样本容量确定的情况下，α与β不能同时增加或减少。
3、统计检验效力（1-β）当H0为假时,得出拒绝H0的正确结论的概率,被称做检验的效力。

• I类错误防范 ：

  • 小概率α设置小些( 避免小概率的触发)
  • 增加样本量（使异常数据的影响降低）

• II类错误防范：

  • 调大α（增加小概率的触发） 但是接受I类错误的代价远比II类错误的代价要大，所以不予使用
  • II类错误概率只能在实验结束后才能计算发生二类错误的概率，这是一个事后值。所以在事前设计我们一般不考虑这个问题。默认二类错误的概率为20%。

样本量计算

统计学上根据统计量抽样分布和边际误差确定样本量
样本量计算工具：http://powerandsamplesize.com/Calculators/Compare-2-Means/2-Sample-Equality

检验策略与实验结果分析

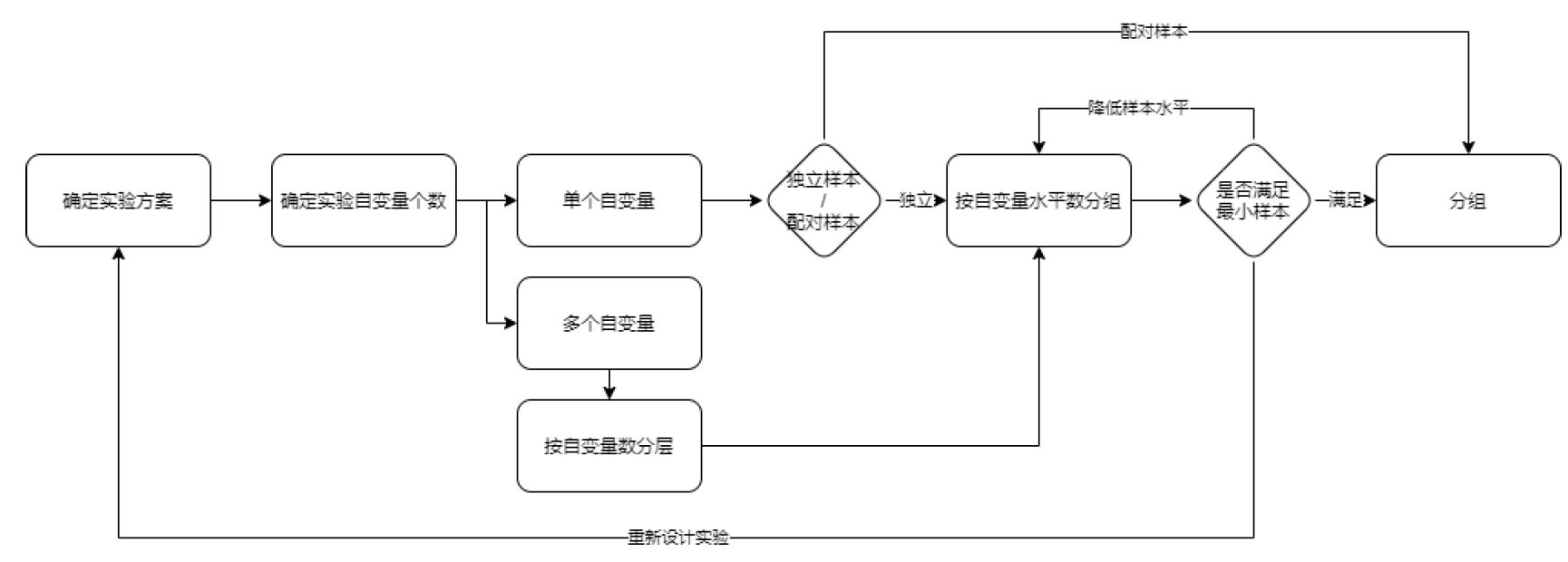
决策业务问题

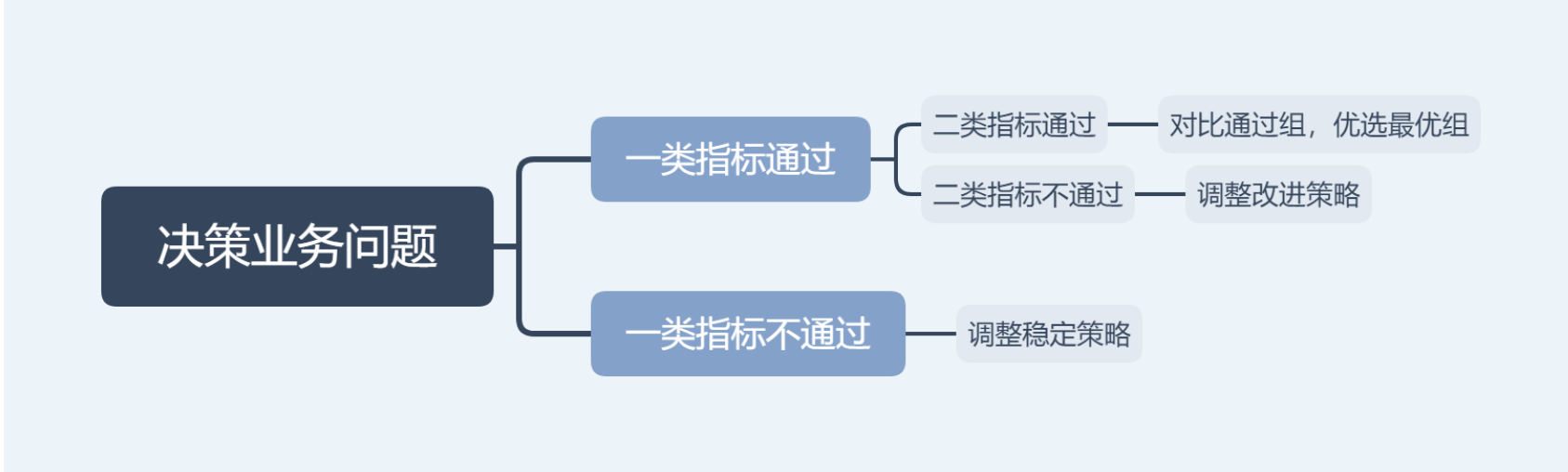
决策统计检验：做实验决策可以通过统计量及统计量的P值来实现。同时也可以通过样本量分布和显著性水平来确定拒绝域和接受域，从而拒绝或者接受结果。见假设检验部分。