BFS

1765. 地图中的最高点

难度中等10收藏分享切换为英文接收动态反馈
给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由 陆地 和 水域 单元格组成的地图。

• 如果 isWater[i][j] == 0 ，格子 (i, j) 是一个 陆地 格子。
• 如果 isWater[i][j] == 1 ，格子 (i, j) 是一个 水域 格子。

你需要按照如下规则给每个单元格安排高度：

• 每个格子的高度都必须是非负的。
• 如果一个格子是是 水域 ，那么它的高度必须为 0 。
• 任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）

找到一种安排高度的方案，使得矩阵中的最高高度值 最大 。
请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：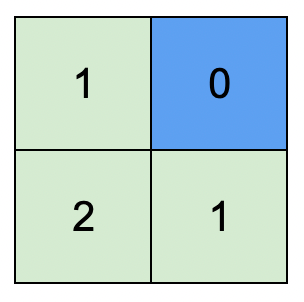

输入：isWater = [[0,1],[0,0]] 输出：[[1,0],[2,1]] 解释：上图展示了给各个格子安排的高度。 蓝色格子是水域格，绿色格子是陆地格。
示例 2：

输入：isWater = [[0,0,1],[1,0,0],[0,0,0]] 输出：[[1,1,0],[0,1,1],[1,2,2]] 解释：所有安排方案中，最高可行高度为 2 。 任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案。

提示：

• m == isWater.length
• n == isWater[i].length
• 1 <= m, n <= 1000
• isWater[i][j] 要么是 0 ，要么是 1 。
• 至少有 1 个水域格子。

/**
 * @param {number[][]} isWater
 * @return {number[][]}
 */
var highestPeak = function(isWater) {
  const result = [];
  const q = [[]];
  for (let i = 0; i < isWater.length; i++) {
    result[i] = [];
    for (let j = 0; j < isWater[i].length; j++) {
      if (isWater[i][j] === 1) {
        q[0].push([i, j]);
        result[i][j] = 0;
      } else {
        result[i][j] = '-';
      }
    }
  }
  const dps = [
    [-1, 0],
    [0, 1],
    [1, 0],
    [0, -1]
  ];
  const rc = isWater.length;
  const rr = isWater[0].length;
  while(q.length) {
    const currentLevels = q.pop();
    const nextLevels = [];
    while(currentLevels.length) {
      const p = currentLevels.pop();
      dps.forEach(dp => {
        const [x, y] = p;
        const [dx, dy] = dp;
        if ((x + dx) < rc && (x + dx) >= 0 &&
          (y + dy) < rr && (y + dy) >= 0 && 
          result[x + dx][y + dy] === '-') {
            nextLevels.push([x + dx, y + dy]);
            result[x + dx][y + dy] = result[x][y] + 1;
          }
      })
    }
    if (nextLevels.length) {
      q.push(nextLevels);
    }
  }
  return result;
};

126. 单词接龙 II

难度困难477收藏分享切换为英文接收动态反馈
按字典 wordList 完成从单词 beginWord 到单词 endWord 转化，一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> … -> sk 这样的单词序列，并满足：

• 每对相邻的单词之间仅有单个字母不同。
• 转换过程中的每个单词 si（1 <= i <= k）必须是字典 wordList 中的单词。注意，beginWord 不必是字典 wordList 中的单词。
• sk == endWord

给你两个单词 beginWord 和 endWord ，以及一个字典 wordList 。请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列 ，如果不存在这样的转换序列，返回一个空列表。每个序列都应该以单词列表 [beginWord, s1, s2, …, sk] 的形式返回。

示例 1：
输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”] 输出：[[“hit”,”hot”,”dot”,”dog”,”cog”],[“hit”,”hot”,”lot”,”log”,”cog”]] 解释：存在 2 种最短的转换序列： “hit” -> “hot” -> “dot” -> “dog” -> “cog” “hit” -> “hot” -> “lot” -> “log” -> “cog”
示例 2：
输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”] 输出：[] 解释：endWord “cog” 不在字典 wordList 中，所以不存在符合要求的转换序列。

提示：

• 1 <= beginWord.length <= 7
• endWord.length == beginWord.length
• 1 <= wordList.length <= 5000
• wordList[i].length == beginWord.length
• beginWord、endWord 和 wordList[i] 由小写英文字母组成
• beginWord != endWord
• wordList 中的所有单词 互不相同

/**
 * @param {string} beginWord
 * @param {string} endWord
 * @param {string[]} wordList
 * @return {string[][]}
 */
var findLadders = function(beginWord, endWord, wordList) {
  if (!wordList.includes(endWord)) {
    return [];
  }
  // 1、convert from wordlist to graph
  const haveEdege = (first, second) => {
    let diff = 0;
    for (let i = 0; i < first.length; i++) {
      if (first[i] !== second[i]) {
        diff += 1;
      }
    }
    return diff === 1;
  };
  const graphs = [];
  let startNode;
  let endNode;
  if (!wordList.includes(beginWord)) {
    wordList.push(beginWord);
  }
  for (let i in wordList) {
    const node = {
      value: wordList[i],
      pos: i,
      level: -1, // BFS 时生成数据，DFS使用level做剪枝判断，避免无脑遍历
      edeges: []
    };
    if (wordList[i] === endWord) {
      endNode = node;
    }
    if (wordList[i] === beginWord) {
      startNode = node;
    }
    graphs.push(node);
  }
  for (let i = 0; i < graphs.length; i++) {
    for (let j = 0; j < graphs.length; j++) {
      if (i === j) {
        continue;
      }
      if (haveEdege(graphs[i].value, graphs[j].value)) {
        if (!graphs[i].edeges.includes(j)) {
          graphs[i].edeges.push(j);
        }
        if (!graphs[j].edeges.includes(i)) {
          graphs[j].edeges.push(i);
        }
      }
    }
  }
  // 2 BFS 查找最短路径长度，为DFS做剪枝使用
  let min = Number.MAX_SAFE_INTEGER;
  let level = 1;
  const bfsQ = [[startNode]];
  while(bfsQ.length) {
    const nodes = bfsQ.shift();
    const nextLevels = [];
    while(nodes.length) {
      const node = nodes.pop();
      node.level = level;
      if (node === endNode) {
        if (min > level) {
          min = level;
        }
      }
      for (let ni of node.edeges) {
        if (graphs[ni].level === -1) {
          graphs[ni].level = level + 1;
          nextLevels.push(graphs[ni]);
        }
      }
    }
    level += 1;
    if (nextLevels.length) {
      bfsQ.push(nextLevels);
    }
  }
  // 3、DFS查找从startNode到endNode的所有最短路径
  const result = [];
  const stack = [{node: startNode, edeges: [...startNode.edeges]}];
  const pop = () => stack.pop();
  const peek = () => stack[stack.length - 1];
  const push = (n) => {
    stack.push(n);
  };
  const makePath = () => {
    const p = [...stack, {node: endNode}].map(i => i.node.value);
    result.push(p);
  };
  while(stack.length) {
    const {node:top, edeges} = peek();
    // 1, 剪枝1，DFS堆栈深度已经超过min，不是目标解，当前栈顶不是目标解，弹出栈顶。
    if (!edeges.length || stack.length >= min) {
      pop();
      continue;
    }
    let next = edeges.pop();
    // 2, 剪枝2，下一跳节点的level比栈顶的节点的level小，说明是该路径不是最短路径，需要剪枝。
    while(graphs[next] && graphs[next].level <= top.level) {
      next = edeges.pop();
    }
    // 3, 剪枝3，找不到下一跳的节点，当前节点元素不是解，弹出栈顶。
    if (next === undefined || graphs[next] === undefined) {
      pop();
      continue;
    }
    if (graphs[next] === endNode) {
      makePath();
      pop();
      continue;
    }
    push({
      node: graphs[next],
      edeges: [...graphs[next].edeges].filter(p => graphs[p].level > top.level)
    });
  }
  return result;
};

127. 单词接龙

难度困难840收藏分享切换为英文接收动态反馈
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列：

• 序列中第一个单词是 beginWord 。
• 序列中最后一个单词是 endWord 。
• 每次转换只能改变一个字母。

• 转换过程中的中间单词必须是字典 wordList 中的单词。

  
  给你两个单词 _beginWord _和 endWord 和一个字典 wordList ，找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0。
  示例 1：
  输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”] 输出：5 解释：一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。
  示例 2：
  输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”] 输出：0 解释：endWord “cog” 不在字典中，所以无法进行转换。

提示：

• 1 <= beginWord.length <= 10
• endWord.length == beginWord.length
• 1 <= wordList.length <= 5000
• wordList[i].length == beginWord.length
• beginWord、endWord 和 wordList[i] 由小写英文字母组成
• beginWord != endWord
• wordList 中的所有字符串 互不相同

/**
 * @param {string} beginWord
 * @param {string} endWord
 * @param {string[]} wordList
 * @return {number}
 */
var ladderLength = function(beginWord, endWord, wordList) {
  if (!wordList.includes(endWord)) {
    return 0;
  }
  if (!wordList.includes(beginWord)) {
    wordList.push(beginWord);
  }
  const haveEdege = (first, second) => {
    let diff = 0;
    for (let i = 0, len = first.length; i < len; i++) {
      if (first[i] !== second[i]) {
        diff += 1;
      }
    }
    return diff === 1;
  };

  let startNode;
  let endNode;
  const graphs = [];
  for (let i = 0, len = wordList.length; i < len; i++) {
    const node = {
      value: wordList[i],
      level: -1,
      edges: []
    };
    if (beginWord === wordList[i]) {
      startNode = node;
    }
    if (endWord === wordList[i]) {
      endNode = node;
    }
    graphs.push(node);
  }

  for (let i = 0, len = graphs.length; i < len; i++) {
    for (let j = i+1; j < len; j++) {
      if (haveEdege(graphs[i].value, graphs[j].value)) {
        if (!graphs[i].edges.includes(j)) {
          graphs[i].edges.push(j);
        }
        if (!graphs[j].edges.includes(i)) {
          graphs[j].edges.push(i);
        }        
      }
    }
  }

  startNode.level = 1;
  let minLen = Number.MAX_SAFE_INTEGER;
  const q = [[startNode]];
  while(q.length) {
    const nodes = q.shift();
    const nextLevels = [];
    while(nodes.length) {
      const node = nodes.shift();
      for (let i = 0, len = node.edges.length; i < len; i++) {
        if (graphs[node.edges[i]].level === -1) {
          graphs[node.edges[i]].level = node.level + 1;
          nextLevels.push(graphs[node.edges[i]]);
          if (graphs[node.edges[i]] === endNode && (node.level + 1 < minLen)) {
            minLen = node.level + 1;
          }
        }
      }
    }
    if (nextLevels.length) {
      q.push(nextLevels);
    }
  }
  return minLen === Number.MAX_SAFE_INTEGER ? 0 : minLen;
};

301. 删除无效的括号

难度困难488收藏分享切换为英文接收动态反馈
给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。

示例 1：
输入：s = “()())()” 输出：[“(())()”,”()()()”]
示例 2：
输入：s = “(a)())()” 输出：[“(a())()”,”(a)()()”]
示例 3：
输入：s = “)(“ 输出：[“”]

提示：

• 1 <= s.length <= 25
• s 由小写英文字母以及括号 ‘(‘ 和 ‘)’ 组成
• s 中至多含 20 个括号

/**
 * @param {string} s
 * @return {string[]}
 */
var removeInvalidParentheses = function(s) {
  const isValid = (str) => {
    const stack = str.split('');
    let left = 0;
    let right = 0;
    for (let i = 0; i < stack.length; i++) {
      const char = str[i];
      if (char !== '(' && char !== ')') {
        continue;
      }

      if (char === '(') {
        left += 1;
      }

      if (char === ')') {
        if (left === 0) {
          return false;
        }
        left  -= 1;
      }
    }
    return left === right && left === 0;
  };
  if (isValid(s)) {
    return [s];
  }  
  const nextLevelStr = (str) => {
    const valids = new Set();
    const inValids = new Set();
    for (let i = 0; i < str.length; i++) {
      if (str[i] === '(' || str[i] === ')') {
        const key = str.substring(0, i) + str.substring(i+1);
        if (isValid(key)) {
          valids.add(key);
        } else {
          inValids.add(key);
        }
      }
    }
    return {valids, inValids};
  };
  const q = [[s]];
  while(q.length) {
    const strs = q.shift();
    const nextLevels = new Set();
    const validsTotal = new Set();
    for (let substr of strs) {
      let {valids, inValids} = nextLevelStr(substr);
      valids.forEach(item => {
        validsTotal.add(item);
      });

      inValids.forEach(item => {
        nextLevels.add(item);
      });
    }
    if (validsTotal.size) {
      return [...validsTotal];
    }
    if (nextLevels.size) {
      q.push(nextLevels);
    }
  }

  if (s.includes('(') || s.includes(')')) {
    return [''];
  }
  return [s];
};

200. 岛屿数量

难度中等1311收藏分享切换为英文接收动态反馈
给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外，你可以假设该网格的四条边均被水包围。

示例 1：
输入：grid = [ [“1”,”1”,”1”,”1”,”0”], [“1”,”1”,”0”,”1”,”0”], [“1”,”1”,”0”,”0”,”0”], [“0”,”0”,”0”,”0”,”0”] ] 输出：1
示例 2：
输入：grid = [ [“1”,”1”,”0”,”0”,”0”], [“1”,”1”,”0”,”0”,”0”], [“0”,”0”,”1”,”0”,”0”], [“0”,”0”,”0”,”1”,”1”] ] 输出：3

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] 的值为 ‘0’ 或 ‘1’

/**
 * @param {character[][]} grid
 * @return {number}
 */
var numIslands = function(grid) {
  if (!grid.length) {
    return 0;
  }
  const m = grid.length;
  const n = grid[0].length;

  let counter = 2;

  const ns = [[-1,0],[1,0],[0,-1],[0,1]];
  const isValidPos = (pos, dpos) => {
    return (pos[0] + dpos[0]) >= 0 &&
      (pos[0] + dpos[0]) < m &&
      (pos[1] + dpos[1]) >= 0 &&
      (pos[1] + dpos[1]) < n;
  };

  const bfs = (i, j, no) => {
    const root = [i, j];
    const qs = [[root]];
    while (qs.length) {
      const nodes = qs.shift();
      const nextLevels = [];
      for (let k = 0; k < nodes.length; k++) {
        const pos = nodes[k];
        if (grid[pos[0]][pos[1]] === no) {
          continue;
        }
        grid[pos[0]][pos[1]] = no;
        for (let p = 0; p < ns.length; p++) {
          const dpos = ns[p];
          if (isValidPos(pos, ns[p]) && grid[pos[0] + dpos[0]][pos[1] + dpos[1]] === '1') {
            nextLevels.push([pos[0] + dpos[0], pos[1] + dpos[1]]);
          }
        }
      }
      if (nextLevels.length) {
        qs.push(nextLevels);
      }
    }
  };

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === counter) {
        continue;
      }
      if (grid[i][j] === '1') {
        counter++;
        bfs(i, j, counter);
      }
    }
  }
  return counter - 2;
};

207. 课程表

难度中等921收藏分享切换为英文接收动态反馈
你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

• 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]] 输出：true 解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。
示例 2：
输入：numCourses = 2, prerequisites = [[1,0],[0,1]] 输出：false 解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

• 1 <= numCourses <= 105
• 0 <= prerequisites.length <= 5000
• prerequisites[i].length == 2
• 0 <= ai, bi < numCourses
• prerequisites[i] 中的所有课程对 互不相同

/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {boolean}
 */
var canFinish = function(numCourses, prerequisites) {
  const ajcList = [];
  for (let i = 0; i < numCourses; i++) {
    ajcList[i] = {
      course: i,
      deps: []
    };
  }

  prerequisites.forEach(([course, dep]) => {
    ajcList[course].deps.push(dep);
  });

  const mems = {};
  const findCycle = (node) => {
    if (mems[node.course]) {
      return true;
    }
    node.visited = true;
    for (let i = 0; i < node.deps.length; i++) {
      if (ajcList[node.deps[i]].visited) {
        return false;
      } else {
        if (!findCycle(ajcList[node.deps[i]])) {
          return false;
        }
      }
    }
    node.visited = false;
    return true;
  };

  // console.log(ajcList);
  for (let i = 0; i < ajcList.length; i++) {
    if (!findCycle(ajcList[i])) {
      return false;
    }
    mems[i] = true;
  }
  return true;
};

210. 课程表 II

难度中等461收藏分享切换为英文接收动态反馈
现在你总共有 n 门课需要选，记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。
示例 1:
输入: 2, [[1,0]] 输出: [0,1] 解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。
示例 2:
输入: 4, [[1,0],[2,0],[3,1],[3,2]] 输出: [0,1,2,3] or [0,2,1,3] 解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。 因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
说明:

1. 输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
2. 你可以假定输入的先决条件中没有重复的边。

提示:

1. 这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
2. 通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。
3. 拓扑排序也可以通过 BFS 完成。

/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {number[]}
 */
var findOrder = function(numCourses, prerequisites) {
  const ajcList = [];
  for (let i = 0; i < numCourses; i++) {
    ajcList.push({
      course: i,
      pre: -1,
      post: -1,
      deps: [],
    });
  }
  prerequisites.forEach(([course, dep]) => {
    ajcList[course].deps.push(dep);
  });

  let clock = 0;
  const mems = [];
  const dfs = (node) => {
    if (mems[node.course]) {
      return true;
    }
    mems[node.course] = true;
    node.visited = true;
    node.pre = clock++;
    for (let i = 0; i < node.deps.length; i++) {
      if (ajcList[node.deps[i]].visited) {
        return false;
      }
      else {
        if (!dfs(ajcList[node.deps[i]])) {
          return false;
        }
      }
    }
    node.post = clock++;
    node.visited = false;
    return true;
  };

  for (let i = 0; i < ajcList.length; i++) {
    if (!mems[i] && !dfs(ajcList[i])) {
      return [];
    }
  }
  return ajcList.sort((a, b) => a.post - b.post).map(item => item.course);
};

310. 最小高度树

难度中等368收藏分享切换为英文接收动态反馈
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。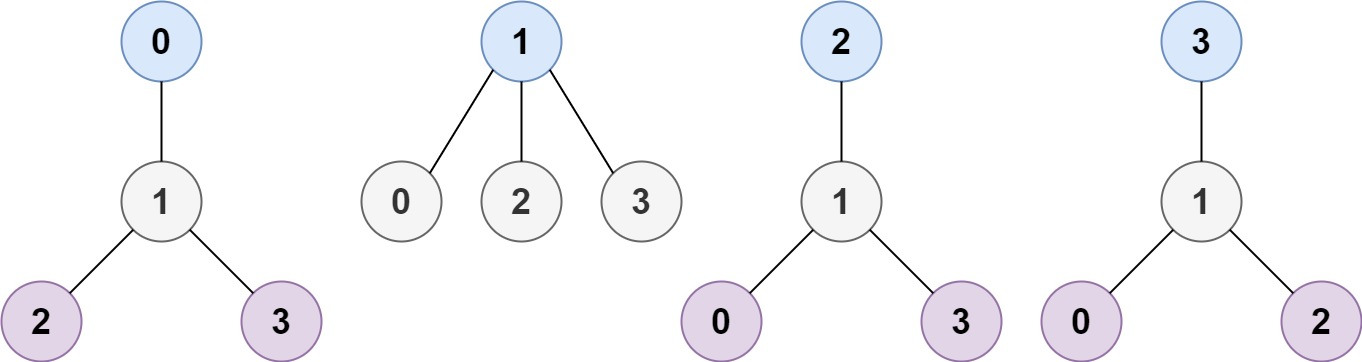
树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。
给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。
请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

示例 1：
输入：n = 4, edges = [[1,0],[1,2],[1,3]] 输出：[1] 解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。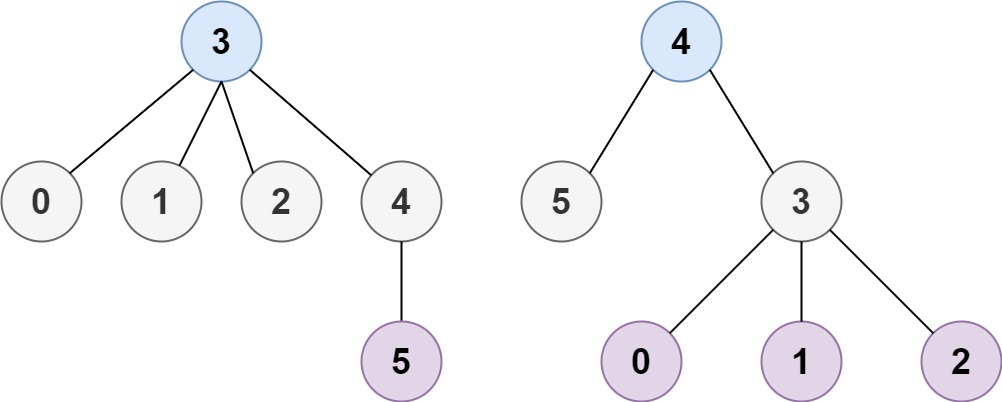

示例 2：
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] 输出：[3,4]
示例 3：
输入：n = 1, edges = [] 输出：[0]
示例 4：
输入：n = 2, edges = [[0,1]] 输出：[0,1]

提示：

• 1 <= n <= 2 * 104
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• 所有 (ai, bi) 互不相同
• 给定的输入 保证 是一棵树，并且 不会有重复的边

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[]}
 */
var findMinHeightTrees = function(n, edges) {
  const results = [];
  if (!edges.length) {
    results.push(0);
    return results;
  }
  const graphs = new Array(n);
  for(let i = 0; i < n; i++) {
    graphs[i] = {
      value: i,
      edges: [],
      degree: 0
    };
  }

  for (let i = 0; i < edges.length; i++) {
    graphs[edges[i][0]].edges.push(edges[i][1]);
    graphs[edges[i][0]].degree++;

    graphs[edges[i][1]].edges.push(edges[i][0]);
    graphs[edges[i][1]].degree++;
  }

  const leafs = [];
  let minDegree = Infinity;
  graphs.forEach(g => {
    if (g.degree < minDegree) {
      minDegree = g.degree;
      leafs.length = 0;
      leafs.push(g);
    } else if (g.degree === minDegree) {
      leafs.push(g);
    }
  });

  const qs = [leafs];

  // console.log('leafs:', leafs);
  while(qs.length) {
    const nodes = qs.shift();
    const nextLevels = [];
    for(let m = 0; m < nodes.length; m++) {
      const node = nodes[m];
      for (let i = 0; i < node.edges.length; i++) {
        let ajc = graphs[node.edges[i]];
        if (ajc.degree > minDegree) {
          ajc.degree--;
          if (ajc.degree === 1) {
            nextLevels.push(graphs[node.edges[i]]);
          }
        }
      }
    }
    results.length = 0;
    if (nextLevels.length) {
      nextLevels.forEach(p => {
        results.push(p.value);
      });
      qs.push(nextLevels);
    } else {
      nodes.forEach(p => {
        results.push(p.value);
      });
    }
  }
  return results;
};

261. 以图判树

难度中等127收藏分享切换为英文接收动态反馈
给定从 0 到 n-1 标号的 n 个结点，和一个无向边列表（每条边以结点对来表示），请编写一个函数用来判断这些边是否能够形成一个合法有效的树结构。
示例 1：
输入: n = 5, 边列表 edges = [[0,1], [0,2], [0,3], [1,4]] 输出: true
示例 2:
输入: n = 5, 边列表 edges = [[0,1], [1,2], [2,3], [1,3], [1,4]] 输出: false
注意：你可以假定边列表 edges 中不会出现重复的边。由于所有的边是无向边，边 [0,1] 和边 [1,0] 是相同的，因此不会同时出现在边列表 edges 中。

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {boolean}
 */
var validTree = function(n, edges) {
  const adList = [];
  adList.length = n;
  for (let i = 0; i < n; i++) {
    adList[i] = [];
  }
  for (let i = 0; i < edges.length; i++) {
    const [first, second] = edges[i];
    adList[first].push(second);
    adList[second].push(first);
  }

  const isCycle = (value, edges, visited, parent) => {
    visited.add(value);
    for (let i = 0; i < edges.length; i++) {
      const current = adList[edges[i]];
      // 与父节点互相有个边
      if (edges[i] === parent) {
        continue;
      }

      if (visited.has(edges[i])) {
        return true;
      }

      if (isCycle(edges[i], current, visited, value)) {
        return true;
      }
    }
    return false;
  };

  let counter = 0;
  const reached = new Set();
  for (let i = 0; i < adList.length; i++) {
    if (reached.has(i)) {
      continue;
    }
    counter ++;
    const visited = new Set();
    if (isCycle(i, adList[i], visited, -1)) {
      return false;
    }
    visited.forEach(p => reached.add(p));
  }
  return counter === 1;
};

286. 墙与门

难度中等163收藏分享切换为英文接收动态反馈
你被给定一个 m × n 的二维网格 rooms ，网格中有以下三种可能的初始化值：

1. -1 表示墙或是障碍物
2. 0 表示一扇门
3. INF 无限表示一个空的房间。然后，我们用 231 - 1 = 2147483647 代表 INF。你可以认为通往门的距离总是小于 2147483647 的。

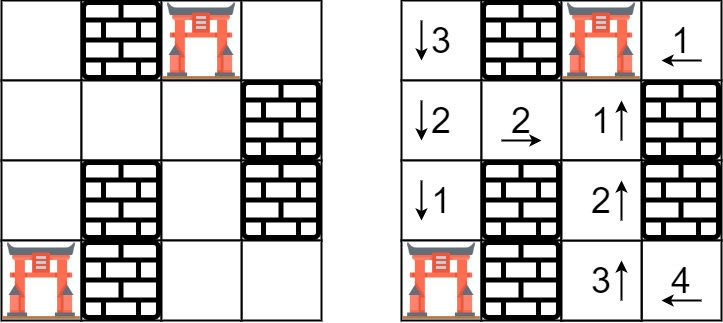
你要给每个空房间位上填上该房间到 最近门的距离 ，如果无法到达门，则填 INF 即可。

示例 1：
输入：rooms = [[2147483647,-1,0,2147483647],[2147483647,2147483647,2147483647,-1],[2147483647,-1,2147483647,-1],[0,-1,2147483647,2147483647]] 输出：[[3,-1,0,1],[2,2,1,-1],[1,-1,2,-1],[0,-1,3,4]]
示例 2：
输入：rooms = [[-1]] 输出：[[-1]]
示例 3：
输入：rooms = [[2147483647]] 输出：[[2147483647]]
示例 4：
输入：rooms = [[0]] 输出：[[0]]

提示：

• m == rooms.length
• n == rooms[i].length
• 1 <= m, n <= 250
• rooms[i][j] 是 -1、0 或 231 - 1

/**
 * @param {number[][]} rooms
 * @return {void} Do not return anything, modify rooms in-place instead.
 */
var wallsAndGates = function(rooms) {
  if (!rooms.length) {
    return [];
  }

  const INF = 2147483647;
  const ns = [[-1, 0],[1,0],[0,-1],[0,1]];
  const m = rooms.length;
  const n = rooms[0].length;
  const doors = [];
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (rooms[i][j] === 0) {
        doors.push([i, j]);
      }
    }
  }
  const isValidPos = (x, y) => {
    return x >= 0 && x < m && y >= 0 && y < n && rooms[x][y] === INF;
  };

  const qs = [doors];
  let level = 0;
  while (qs.length) {
    const nodes = qs.shift();
    const nextLevels = [];
    while (nodes.length) {
      const pos = nodes.shift();
      for (let m = 0; m < ns.length; m++) {
        const x = pos[0] + ns[m][0];
        const y = pos[1] + ns[m][1];        
        if (isValidPos(x, y)) {
          nextLevels.push([x, y]);
          rooms[x][y] = level + 1;
        }
      }
    }
    level++;
    if (nextLevels.length) {
      qs.push(nextLevels);
    }
  }
  // console.log(rooms);
  return rooms;
};

317. 离建筑物最近的距离

难度困难101收藏分享切换为英文接收动态反馈
你是个房地产开发商，想要选择一片空地 建一栋大楼。你想把这栋大楼够造在一个距离周边设施都比较方便的地方，通过调研，你希望从它出发能在 最短的距离和 内抵达周边全部的建筑物。请你计算出这个最佳的选址到周边全部建筑物的 最短距离和。

提示：
你只能通过向上、下、左、右四个方向上移动。
给你一个由 0、1 和 2 组成的二维网格，其中：

• 0 代表你可以自由通过和选择建造的空地
• 1 代表你无法通行的建筑物
• 2 代表你无法通行的障碍物

示例：

输入：[[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]]

1 - 0 - 2 - 0 - 1
|   |   |   |   |
0 - 0 - 0 - 0 - 0
|   |   |   |   |
0 - 0 - 1 - 0 - 0
输出：7 
解析：
给定三个建筑物 (0,0)、(0,4) 和 (2,2) 以及一个位于 (0,2) 的障碍物。
由于总距离之和 3+3+1=7 最优，所以位置 (1,2) 是符合要求的最优地点，故返回7。

注意：

• 题目数据保证至少存在一栋建筑物，如果无法按照上述规则返回建房地点，则请你返回 -1。

  /**
  * @param {number[][]} grid
  * @return {number}
  */
  var shortestDistance = function(grid) {
  if (!grid.length) {
    return -1;
  }
  const m = grid.length;
  const n = grid[0].length;
  
  const buildings = [];
  const dMaps = [];
  for (let i = 0; i < m; i ++) {
    dMaps[i] = [];
    dMaps[i].length = n;
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === 1) {
        buildings.push([i, j]);
      }
      if (grid[i][j] === 0) {
        dMaps[i][j] = {
          value: 0,
          visited: 0
        };
      }
    }
  }
  const ns = [[-1,0],[1,0],[0,-1],[0,1]];
  
  const isValid = (x, y) => {
    return x >= 0 && x < m && y >= 0 && y < n && dMaps[x][y];
  };
  
  const hasVisited = (x, y, visited) => visited[x][y];
  
  const makeVisited = () => {
    const visited = [];
    visited.length = m;
    for (let j = 0; j < m; j++) {
      visited[j] = [];
      visited[j].length = n;
    }
    return visited;
  };
  
  const inNextLevels = (x, y, nextLevels) => {
    return nextLevels.find(([ix, iy]) => ix === x && iy === y);
  };
  
  // console.log('fill distances');
  for (let b = 0; b < buildings.length; b++) {
    let level = 0;
    const visited = makeVisited();
    const block = buildings[b];
    // console.log('for building:', block);
    const qs = [[block]];
    while (qs.length) {
      const nodes = qs.shift();
      const nextLevels = [];
      while (nodes.length) {
        const [bx, by] = nodes.shift();
        visited[bx][by] = true;
        for (let i = 0; i < ns.length; i++) {
          const x = bx + ns[i][0];
          const y = by + ns[i][1];
          if (isValid(x, y) && !hasVisited(x, y, visited) && !inNextLevels(x, y, nextLevels)) {
            dMaps[x][y].value += level + 1;
            dMaps[x][y].visited++;
            nextLevels.push([x,y]);
          }
        }
      }
      level++;
      if (nextLevels.length) {
        qs.push(nextLevels);
      }
    }
    // console.log(dMaps.map(p => p.map(i => `${i.value}:${i.visited}`).join(' ')));
  }
  
  // console.log(dMaps);
  let min = Infinity;
  for (let i = 0; i < dMaps.length; i++) {
    for (let j = 0; j < dMaps[i].length; j++) {
      const r = dMaps[i][j];
      if (r && r.visited === buildings.length && r.value < min) {
        min = r.value;
      }
    }
  }
  min = min === Infinity ? -1 : min;
  // console.log('min:', min);
  return min;
  };
  

429. N 叉树的层序遍历

难度中等171收藏分享切换为英文接收动态反馈
给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。
树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：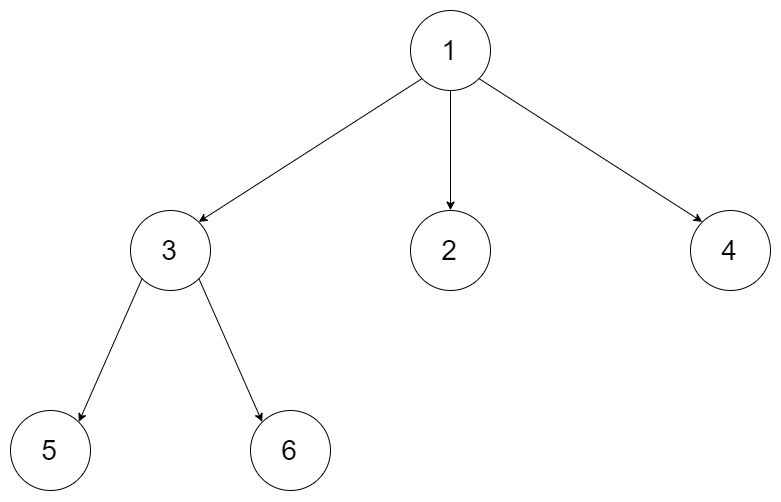

输入：root = [1,null,3,2,4,null,5,6] 输出：[[1],[3,2,4],[5,6]]
示例 2：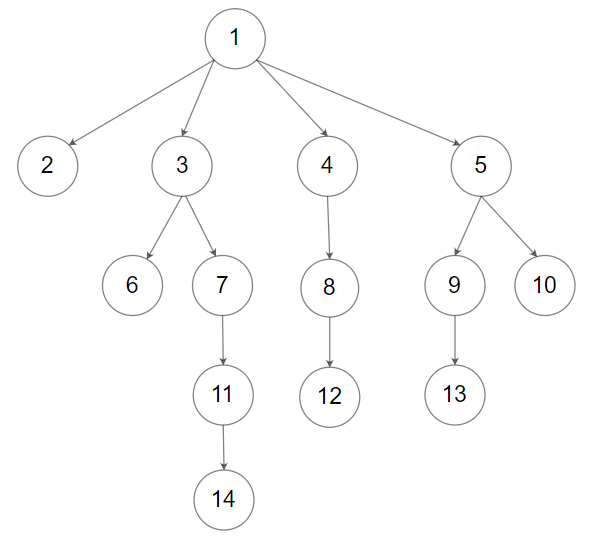

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

• 树的高度不会超过 1000
• 树的节点总数在 [0, 10^4] 之间

/**
 * // Definition for a Node.
 * function Node(val,children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */

/**
 * @param {Node|null} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    if (!root) {
        return [];
    }
    const q = [[root]];
    let top = 0;
    while (q[top].length) {
        const nextLevels = [];
        const nodes = q[top];
        for (let n = 0; n < nodes.length; n++) {
            if (nodes[n].children) {
                for (let i = 0; i < nodes[n].children.length; i++) {
                    if (nodes[n].children?.[i]) {
                        nextLevels.push(nodes[n].children[i]);
                    }
                }
            }
        }
        if (!nextLevels.length) {
            break;
        }
        top++;
        q.push(nextLevels);
    }
    return q.map(nodes => {
        return nodes.map(n => n.val);
    });
};

102. 二叉树的层序遍历

难度中等987收藏分享切换为英文接收动态反馈
给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：
二叉树：[3,9,20,null,null,15,7],
3 / \ 9 20 / \ 15 7
返回其层序遍历结果：
[ [3], [9,20], [15,7] ]

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    if (!root) {
        return [];
    }
    const q = [[root]];
    const r = [[root.val]];
    while(q.length) {
        const nodes = q.shift();
        const nextlevels = [];
        for (let node of nodes) {
            if (node && node.left) {
                nextlevels.push(node.left);
            }
            if (node && node.right) {
                nextlevels.push(node.right);
            }
        }
        if (nextlevels.length) {
            q.push(nextlevels);
            r.push(nextlevels.map(n => n.val));
        }
    }
    return r;
};

107. 二叉树的层序遍历 II

难度中等473收藏分享切换为英文接收动态反馈
给定一个二叉树，返回其节点值自底向上的层序遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）
例如：
给定二叉树 [3,9,20,null,null,15,7],
3 / \ 9 20 / \ 15 7
返回其自底向上的层序遍历为：
[ [15,7], [9,20], [3] ]

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrderBottom = function(root) {
    if (!root) {
        return [];
    }
    const q = [[root]];
    const ret = [[root.val]];

    while (q.length) {
        const nodes = q.shift();
        const nextLevels = [];
        for (let node of nodes) {
            if (node && node.left) {
                nextLevels.push(node.left);
            }
            if (node && node.right) {
                nextLevels.push(node.right);
            }
        }
        if (nextLevels.length) {
            q.push(nextLevels);
            ret.push(nextLevels.map(n => n.val));
        }
    }

    return ret.reverse();
};

剑指 Offer 32 - I. 从上到下打印二叉树

难度中等120收藏分享切换为英文接收动态反馈
从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回：
[3,9,20,15,7]

提示：

1. 节点总数 <= 1000

   /**
   * Definition for a binary tree node.
   * function TreeNode(val) {
   *     this.val = val;
   *     this.left = this.right = null;
   * }
   */
   /**
   * @param {TreeNode} root
   * @return {number[]}
   */
   var levelOrder = function(root) {
    if (!root) {
        return [];
    }
   
    const q = [root];
    let top = 0;
    while ( top < q.length) {
        const node = q[top];
        if (node && node.left) {
            q.push(node.left);
        }
        if (node && node.right) {
            q.push(node.right);
        }
        top += 1;
    }
    return q.map(n => n.val);
   };
   

   剑指 Offer 32 - III. 从上到下打印二叉树 III

   难度中等127收藏分享切换为英文接收动态反馈
   请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果：

[
[3],
[20,9],
[15,7]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/cong-shang-dao-xia-da-yin-er-cha-shu-iii-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

提示：

1. 节点总数 <= 1000

   /**
   * Definition for a binary tree node.
   * function TreeNode(val) {
   *     this.val = val;
   *     this.left = this.right = null;
   * }
   */
   /**
   * @param {TreeNode} root
   * @return {number[][]}
   */
   var levelOrder = function(root) {
    if (!root) {
        return [];
    }
   
    const q = [[root]];
    const r = [[root.val]];
   
    let leftToRight = false;
    while (q.length) {
        const nodes = q.shift();
        const nextLevels = [];
        for (let node of nodes) {
            if (node && node.left) {
                nextLevels.push(node.left);
            }
            if (node && node.right) {
                nextLevels.push(node.right);
            }
        }
        if (nextLevels.length) {
            q.push(nextLevels);
            if (leftToRight) {
                r.push(nextLevels.map(nn => nn.val));
            } else {
                r.push(nextLevels.map(nn => nn.val).reverse());
            }            
            leftToRight = !leftToRight;
   
        }
    }
   
    return r;
   };
   

103. 二叉树的锯齿形层序遍历

难度中等508收藏分享切换为英文接收动态反馈
给定一个二叉树，返回其节点值的锯齿形层序遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。
例如：
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层序遍历如下：

[
[3],
[20,9],
[15,7]
]

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var zigzagLevelOrder = function(root) {
    if (!root) {
        return [];
    }

    const q = [[root]];
    const r = [[root.val]];

    let leftToRight = false;
    while (q.length) {
        const nodes = q.shift();
        const nextLevels = [];
        for (let node of nodes) {
            if (node && node.left) {
                nextLevels.push(node.left);
            }
            if (node && node.right) {
                nextLevels.push(node.right);
            }
        }
        if (nextLevels.length) {
            q.push(nextLevels);
            if (leftToRight) {
                r.push(nextLevels.map(nn => nn.val));
            } else {
                r.push(nextLevels.map(nn => nn.val).reverse());
            }            
            leftToRight = !leftToRight;

        }
    }

    return r;
};

993. 二叉树的堂兄弟节点

难度简单229收藏分享切换为英文接收动态反馈
在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

示例 1：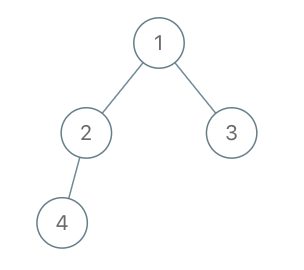

输入：root = [1,2,3,4], x = 4, y = 3 输出：false
示例 2：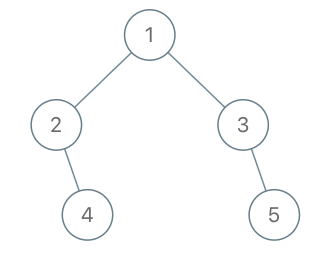

输入：root = [1,2,3,null,4,null,5], x = 5, y = 4 输出：true
示例 3：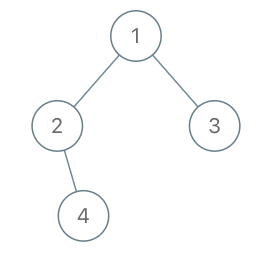

输入：root = [1,2,3,null,4], x = 2, y = 3 输出：false

提示：

• 二叉树的节点数介于 2 到 100 之间。

• 每个节点的值都是唯一的、范围为 1 到 100 的整数。 ```javascript /**

  • Definition for a binary tree node.
  • function TreeNode(val, left, right) {
  • this.val = (val===undefined ? 0 : val)
  • this.left = (left===undefined ? null : left)
  • this.right = (right===undefined ? null : right)
  • } / /*
  • @param {TreeNode} root
  • @param {number} x
  • @param {number} y

  • @return {boolean} */ var isCousins = function(root, x, y) { if (!root) {

    return false;
    

    }

    const q = [[root]]; let findXyResult = []; let depth = 0; while (q.length) {

    const nodes = q.shift();
    const nextLevels = [];
    for (let node of nodes) {
        if (node && node.left) {
            nextLevels.push(node.left);
            findXy(node.left, node, x, y, depth, findXyResult);
        }
        if (node && node.right) {
            nextLevels.push(node.right);
            findXy(node.right, node,  x, y, depth, findXyResult);
        }            
    }
    
    if (nextLevels.length) {
        q.push(nextLevels);
        depth += 1;
    }
    

    }

    return checkResult(findXyResult); };

function checkResult(findXyResult) { if (findXyResult.length === 2) { if (findXyResult[0][0] === findXyResult[1][0]) { return false; }

    if (findXyResult[0][1] !== findXyResult[1][1]) {
        return false;
    }
    return true;
}
return false;

}

function findXy(node, parent, x, y, depth, findXyResult) { if (node.val === x) { findXyResult.push([parent.val, depth + 1]); } if (node.val === y) { findXyResult.push([parent.val, depth + 1]); } }

<a name="uO3Nq"></a>
#### [323. 无向图中连通分量的数目](https://leetcode-cn.com/problems/number-of-connected-components-in-an-undirected-graph/)
难度中等96收藏分享切换为英文接收动态反馈<br />给定编号从 0 到 n-1 的 n 个节点和一个无向边列表（每条边都是一对节点），请编写一个函数来计算无向图中连通分量的数目。<br />**示例 1:**<br />输入: n = 5 和 edges = [[0, 1], [1, 2], [3, 4]]

     0             3<br />     |              |<br />     1 --- 2    4 

输出: 2

**示例 2:**<br />输入: n = 5 和 edges = [[0, 1], [1, 2], [2, 3], [3, 4]]

     0               4<br />     |                |<br />     1 --- 2 --- 3

输出:  1

**注意:**<br />你可以假设在 edges 中不会出现重复的边。而且由于所以的边都是无向边，[0, 1] 与 [1, 0]  相同，所以它们不会同时在 edges 中出现。

```javascript
/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number}
 */
var countComponents = function(n, edges) {

    const graphs = [];
    graphs.length = n;

    for (let [from, to] of edges) {
        graphs[from] = graphs[from] || [];
        graphs[from].push(to);

        graphs[to] = graphs[to] || [];
        graphs[to].push(from);
    }

    const visited = [];
    visited.length = n;
    visited.fill(false);
    let count = 0;
    for (let i = 0; i < graphs.length; i++) {
        if (!visited[i]) {
            bfs(graphs, i, visited);
            count += 1;
        }
    }
    return count;
};

function bfs(graphs, i, visited) {
    const q = [[i]];
    visited[i] = true;
    while (q.length) {
        const nodes = q.shift();
        const nextLevels = [];
        for (let node of nodes) {
            if (graphs[node] && graphs[node].length) {
                for (let j = 0; j < graphs[node].length; j++) {
                    if (!visited[graphs[node][j]]) {
                        nextLevels.push(graphs[node][j]);
                        visited[graphs[node][j]] = true;
                    }
                }
            }
        }

        if (nextLevels.length) {
            q.push(nextLevels);
        }
    }
}

695. 岛屿的最大面积

难度中等546收藏分享切换为英文接收动态反馈
给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。
示例 2:
[[0,0,0,0,0,0,0,0]]
对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxAreaOfIsland = function(grid) {
    let max = 0;
    for (let i = 0; i < grid.length; i++) {
        for (let j = 0; j < grid[i].length; j++) {
            if (grid[i][j] === 1) {
                max = Math.max(max, bfs(grid, i, j));
            }
        }
    }
    return max;
};

function bfs(grid, i, j) {
    const q = [[[i, j]]];
    let count = 1;
    const positions = [
        [-1, 0],
        [1, 0],
        [0, -1],
        [0, 1]
    ];
    const isValidPos = (x, y) => {
        return x < grid.length 
            && x >= 0 
            && y < grid[0].length 
            && y >= 0;
    };
    grid[i][j] = 0;
    while (q.length) {
        const nodes = q.shift();
        const nextLevels = [];
        for (let [x, y] of nodes) {
            for (let [dx, dy] of positions) {
                if (isValidPos(x + dx, y + dy) && grid[x + dx][y + dy] === 1) {
                    count += 1;
                    nextLevels.push([x + dx, y + dy]);
                    grid[x + dx][y + dy] = 0;
                }
            }
        }
        if (nextLevels.length) {
            q.push(nextLevels);
        }
    }
    return count;
}

417. 太平洋大西洋水流问题

难度中等280收藏分享切换为英文接收动态反馈
给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。
规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。
请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标。

提示：

1. 输出坐标的顺序不重要
2. m 和 n 都小于150

示例：

给定下面的 5x5 矩阵:

太平洋 ~ ~ ~ ~ ~
~ 1 2 2 3 (5)
~ 3 2 3 (4) (4)
~ 2 4 (5) 3 1
~ (6) (7) 1 4 5
~ (5) 1 1 2 4
大西洋

返回:

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).

/**
 * @param {number[][]} heights
 * @return {number[][]}
 */
var pacificAtlantic = function (heights) {
  const { m, n, pround, around } = initBoundary(heights);
  const visited = initVisited(m, n, pround, around);
  // bfs from pacific
  bfs(pround, heights, ([nx, ny]) => {
    const old = visited[nx][ny];
    const diff = old === 0 || old === 2 ? 1 : 0;
    visited[nx][ny] += diff;
    if (diff === 1) {
      return [nx, ny];
    }
  });

  // bfs from atlantic
  bfs(around, heights, ([nx, ny]) => {
    const old = visited[nx][ny];
    const diff = old === 0 || old === 1 ? 2 : 0;
    visited[nx][ny] += diff;
    if (diff === 2) {
      return [nx, ny];
    }
  });
  return findResult(m, n, visited);
};
function initVisited(m, n, pround, around) {
  const visited = new Array(m);
  for (let i = 0; i < m; i++) {
    visited[i] = [];
    visited[i].length = n;
    for (let j = 0; j < n; j++) {
      visited[i][j] = 0;
    }
  }
  pround.forEach(([x, y]) => {
    visited[x][y] += 1;
  });
  around.forEach(([x, y]) => {
    visited[x][y] += 2;
  });  
  return visited;
}
function bfsTemplate(rootlevels, nodeVisitor) {
  const q = [rootlevels];
  while (q.length) {
    const nodes = q.shift();
    const nextLevels = [];
    for (let node of nodes) {
      const r = nodeVisitor(node);
      if (r && Array.isArray(r) && r.length) {
        nextLevels.push(...r);
      }
    }
    if (nextLevels.length) {
      q.push(nextLevels);
    }
  }
}

function initBoundary(heights) {
  const m = heights.length;
  const n = heights[0].length;
  const pround = [];
  const around = [];
  for (let i = 0; i < n; i++) {
    pround.push([0, i]);
    around.push([m - 1, i]);
  }
  const isSame = (x, y) => {
    return ([ix, iy]) => x === ix && iy === y;
  };

  for (let i = 0; i < m; i++) {
    if (!pround.find(isSame(i, 0))) {
      pround.push([i, 0]);
    }

    if (!around.find(isSame(i, n - 1))) {
      around.push([i, n - 1]);
    }
  }
  return { m, n, pround, around };
}

function findResult(m, n, visited) {
  const result = [];
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (visited[i][j] >= 3) {
        result.push([i, j]);
      }
    }
  }
  return result;
}

function isBoundry(m, n, nx, ny) {
  return (nx === m - 1 && ny === 0) || (nx === 0 && ny === n - 1);
}

const positions = [
  [-1, 0],
  [1, 0],
  [0, -1],
  [0, 1],
];

function bfs(round, heights, checkCell) {
  const m = heights.length;
  const n = heights[0].length;
  const mapPosition = ([x, y]) => ([dx, dy]) => {
    const nx = x + dx;
    const ny = y + dy;
    const r = nx >= 0 && ny >= 0 && nx < m && ny < n && (
      heights[nx][ny] >= heights[x][y] || isBoundry(m, n, nx, ny)
    );
    if (r) {
      return [nx, ny];
    }
    return null;
  };

  bfsTemplate(round, (pos) => {
    return positions
      .map(mapPosition(pos))
      .filter(Boolean)
      .reduce((nextLevels, npos) => {
        const r = checkCell(npos);
        if (r) {
          nextLevels.push(r);
        }
        return nextLevels;
      }, []);
  }); 
}

130. 被围绕的区域

难度中等603收藏分享切换为英文接收动态反馈
给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ ，找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。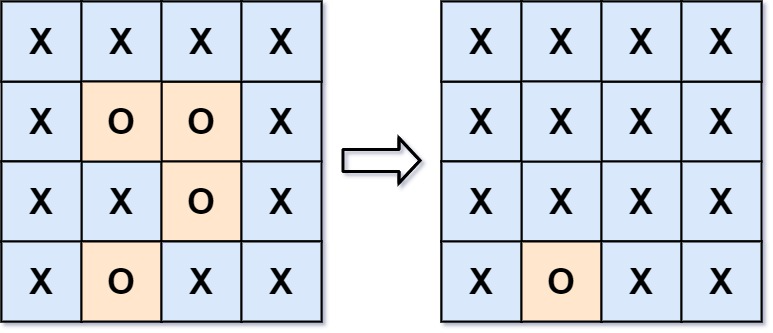

示例 1：
输入：board = [[“X”,”X”,”X”,”X”],[“X”,”O”,”O”,”X”],[“X”,”X”,”O”,”X”],[“X”,”O”,”X”,”X”]]
输出：[[“X”,”X”,”X”,”X”],[“X”,”X”,”X”,”X”],[“X”,”X”,”X”,”X”],[“X”,”O”,”X”,”X”]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：
输入：board = [[“X”]] 输出：[[“X”]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 为 ‘X’ 或 ‘O’

/**
 * @param {character[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
var solve = function(board) {
    const m = board.length;
    const n = board[0].length;
    const holds = new Array(m); // -1 hold, 0 no visited 1 visited
    const rounds = [];

    for (let i = 0; i < m; i++) {
        holds[i] = [];
        for (let j = 0; j < n; j++) {
            holds[i][j] = 0;
            if (board[i][j] === 'O' && (i === 0 || i === m - 1 || j === 0 || j === n-1)) {
                rounds.push([i, j]);
                holds[i][j] = -1;
            }
        }
    }

    const isValidPos = (pos, dpos) => {
        return (pos[0] + dpos[0]) >= 0 && (pos[1] + dpos[1]) >= 0 &&
            (pos[0] + dpos[0]) < m && (pos[1] + dpos[1]) < n;
    };

    const positions = [
        [-1, 0],
        [1, 0],
        [0, 1],
        [0, -1]
    ];
    // console.log(holds);
    // console.log(rounds);
    const q = [rounds];
    while (q.length) {
        const nodes = q.shift();
        const nextLevels = [];
        for (let [i, j] of nodes) {
            for (let dpos of positions) {
                if (isValidPos([i,j], dpos) && board[i + dpos[0]][j + dpos[1]] === 'O') {
                    if (holds[i + dpos[0]][j + dpos[1]] === 0) {
                        holds[i + dpos[0]][j + dpos[1]] = -1;
                        nextLevels.push([i + dpos[0], j + dpos[1]]);
                    }
                }
            }
        }
        if (nextLevels.length) {
            q.push(nextLevels);
        }
    }

    // console.log(holds);
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (holds[i][j] !== -1) {
                board[i][j] = 'X'; 
            }
        }
    }
 };

934. 最短的桥

难度中等184收藏分享切换为英文接收动态反馈
在给定的二维二进制数组 A 中，存在两座岛。（岛是由四面相连的 1 形成的一个最大组。）
现在，我们可以将 0 变为 1，以使两座岛连接起来，变成一座岛。
返回必须翻转的 0 的最小数目。（可以保证答案至少是 1 。）

示例 1：
输入：A = [[0,1],[1,0]] 输出：1
示例 2：
输入：A = [[0,1,0],[0,0,0],[0,0,1]] 输出：2
示例 3：
输入：A = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]] 输出：1

提示：

• 2 <= A.length == A[0].length <= 100
• A[i][j] == 0 或 A[i][j] == 1

/**
 * @param {number[][]} grid
 * @return {number}
 */
var shortestBridge = function(grid) {
  const m = grid.length;
  const n = grid[0].length;
  const visited = new Array(m);
  const eachCell = (grid, callback) => {
    const m = grid.length;
    const n = grid[0].length;
    for (let i = 0 ; i < m; i++) {
      for (let j = 0; j < n; j++) {
        callback([i, j], grid[i][j], grid);
      }
    }
  };

  let first = [-1, -1];
  eachCell(grid, ([i, j], val) => {
    if (!visited[i]) {
      visited[i] = new Array(n).fill(false);
    }
    if (val === 1 && !visited[i][j]) {
      first[0] = i;
      first[1] = j;
    }
  });


  const positions = [
    [-1, 0], [1, 0], [0, -1], [0, 1]
  ];
  const isValidPos = (pos, dpos) => {
    return pos[0] + dpos[0] >= 0 &&
      pos[1] + dpos[1] >= 0 &&
      pos[0] + dpos[0] < m &&
      pos[1] + dpos[1] < n;
  }

  const bfsWithMark = (nodes, visited) => {
    const q = [nodes];
    const islands = [...nodes];
    while (q.length) {
      const nodes = q.shift();
      const nextLevels = [];

      for (let [i, j] of nodes) {
        visited[i][j] = true;
        for (let dpos of positions) {
          if (isValidPos([i, j], dpos) && 
            !visited[i + dpos[0]][j + dpos[1]] &&
            grid[i + dpos[0]][j + dpos[1]] === 1) {
            islands.push([i + dpos[0], j + dpos[1]]);
            nextLevels.push([i + dpos[0], j + dpos[1]]);
            visited[i + dpos[0]][j + dpos[1]] = true;
          }
        }
      }

      if (nextLevels.length) {
        q.push(nextLevels);
      }
    }
    return islands;
  };
  const bfs = (nodes, visited) => {
    const q = [nodes];
    let levels = 0;
    let min = Number.MAX_SAFE_INTEGER;
    while (q.length) {
      const nodes = q.shift();
      const nextLevels = [];

      for (let [i, j] of nodes) {
        for (let dpos of positions) {
          if (isValidPos([i, j], dpos) && 
            !visited[i + dpos[0]][j + dpos[1]]) {
            const nextValue = grid[i + dpos[0]][j + dpos[1]];
            if (nextValue === 0) {
              nextLevels.push([i + dpos[0], j + dpos[1]]);
            } else if (nextValue === 1) {
              min = Math.min(min, levels);
            }
            visited[i + dpos[0]][j + dpos[1]] = true;
          }
        }
      }

      if (nextLevels.length) {
        q.push(nextLevels);
        levels += 1;
      }
    }
    return min;
  };

  const islands = bfsWithMark([first], visited);
  const r = bfs(islands, visited);
  return r;
};

1020. 飞地的数量

难度中等53收藏分享切换为英文接收动态反馈
给出一个二维数组 A，每个单元格为 0（代表海）或 1（代表陆地）。
移动是指在陆地上从一个地方走到另一个地方（朝四个方向之一）或离开网格的边界。
返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：
输入：[[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]] 输出：3 解释： 有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。
示例 2：
输入：[[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]] 输出：0 解释： 所有 1 都在边界上或可以到达边界。

提示：

1. 1 <= A.length <= 500
2. 1 <= A[i].length <= 500
3. 0 <= A[i][j] <= 1
4. 所有行的大小都相同

/**
 * @param {number[][]} grid
 * @return {number}
 */
var numEnclaves = function (grid) {
    const m = grid.length;
    const n = grid[0].length;
    const positions = [
        [-1, 0], [1, 0], [0, -1], [0, 1]
    ];

    const isValidPos = (i, j) => {
        return i >= 0 && j >= 0 && j < n && i < m;
    };
    for (let i = 0; i < n; i++) {
        if (grid[0][i] === 1) {
            bfs(0, i, 2);
        }
        if (grid[m-1][i] === 1) {
            bfs(m-1, i, 2);
        }
    }
    for (let i = 0; i < m; i++) {
        if (grid[i][0] === 1) {
            bfs(i, 0, 2);
        }
        if (grid[i][n-1] === 1) {
            bfs(i, n-1, 2);
        }
    }
    let count = 0;
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] === 1) {
                // console.log(count, grid.map(item => item.join(',')));
                count += 1;
            }
        }
    }

    function bfs(i, j, val) {
        grid[i][j] = val;
        const q = [[i, j]];
        while (q.length) {
            const [x, y] = q.shift();
            for (let n = 0; n < positions.length; n++) {
                const [dx, dy] = positions[n];
                if (isValidPos(x + dx, y + dy) && grid[x + dx][y + dy] === 1) {
                    grid[x + dx][y + dy] = val;
                    q.push([x + dx, y + dy]);
                }
            }
        }
    };
    // console.log(grid.map(item => item.join(',')));
    return count;
};

1254. 统计封闭岛屿的数目

难度中等88收藏分享切换为英文接收动态反馈
有一个二维矩阵 grid ，每个位置要么是陆地（记号为 0 ）要么是水域（记号为 1 ）。
我们从一块陆地出发，每次可以往上下左右 4 个方向相邻区域走，能走到的所有陆地区域，我们将其称为一座「岛屿」。
如果一座岛屿 完全 由水域包围，即陆地边缘上下左右所有相邻区域都是水域，那么我们将其称为 「封闭岛屿」。
请返回封闭岛屿的数目。

示例 1：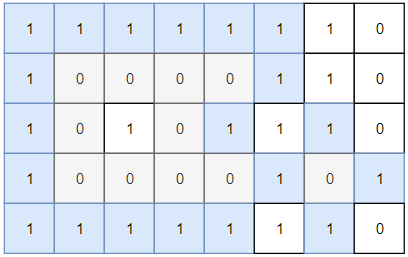

输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] 输出：2 解释： 灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。
示例 2：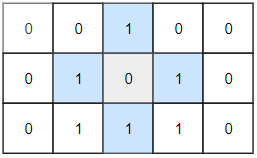

输入：grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]] 输出：1
示例 3：
输入：grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
输出：2

提示：

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <=1

/**
 * @param {number[][]} grid
 * @return {number}
 */
var closedIsland = function(grid) {
    const m = grid.length;
    const n = grid[0].length;
    const positions = [
        [-1, 0], [1, 0], [0, -1], [0, 1]
    ];

    const isValidPos = (i, j) => {
        return i >= 0 && j >= 0 && j < n && i < m;
    };
    for (let i = 0; i < n; i++) {
        if (grid[0][i] === 0) {
            bfs(0, i, 1);
        }
        if (grid[m-1][i] === 0) {
            bfs(m-1, i, 1);
        }
    }
    for (let i = 0; i < m; i++) {
        if (grid[i][0] === 0) {
            bfs(i, 0, 1);
        }
        if (grid[i][n-1] === 0) {
            bfs(i, n-1, 1);
        }
    }
    let count = 0;
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] === 0) {
                // console.log(count, grid.map(item => item.join(',')));
                count += 1;
                bfs(i, j, 1);
            }
        }
    }

    function bfs(i, j, val) {
        grid[i][j] = val;
        const q = [[i, j]];
        while (q.length) {
            const [x, y] = q.shift();
            for (let n = 0; n < positions.length; n++) {
                const [dx, dy] = positions[n];
                if (isValidPos(x + dx, y + dy) && grid[x + dx][y + dy] === 0) {
                    grid[x + dx][y + dy] = val;
                    q.push([x + dx, y + dy]);
                }
            }
        }
    };
    // console.log(grid.map(item => item.join(',')));
    return count;
};

1034. 边框着色

难度中等26收藏分享切换为英文接收动态反馈
给出一个二维整数网格 grid，网格中的每个值表示该位置处的网格块的颜色。
只有当两个网格块的颜色相同，而且在四个方向中任意一个方向上相邻时，它们属于同一连通分量。
连通分量的边界是指连通分量中的所有与不在分量中的正方形相邻（四个方向上）的所有正方形，或者在网格的边界上（第一行/列或最后一行/列）的所有正方形。
给出位于 (r0, c0) 的网格块和颜色 color，使用指定颜色 color 为所给网格块的连通分量的边界进行着色，并返回最终的网格 grid 。

示例 1：
输入：grid = [[1,1],[1,2]], r0 = 0, c0 = 0, color = 3 输出：[[3, 3], [3, 2]]
示例 2：
输入：grid = [[1,2,2],[2,3,2]], r0 = 0, c0 = 1, color = 3 输出：[[1, 3, 3], [2, 3, 3]]
示例 3：
输入：grid = [[1,1,1],[1,1,1],[1,1,1]], r0 = 1, c0 = 1, color = 2 输出：[[2, 2, 2], [2, 1, 2], [2, 2, 2]]

提示：

1. 1 <= grid.length <= 50
2. 1 <= grid[0].length <= 50
3. 1 <= grid[i][j] <= 1000
4. 0 <= r0 < grid.length
5. 0 <= c0 < grid[0].length
6. 1 <= color <= 1000

/**
 * @param {number[][]} grid
 * @param {number} r0
 * @param {number} c0
 * @param {number} color
 * @return {number[][]}
 */
var colorBorder = function(grid, r0, c0, color) {
    const m = grid.length;
    const n = grid[0].length;

    const target = grid[r0][c0];
    const q = [[r0, c0]];

    const positions = [
        [-1, 0], [1, 0], [0, -1], [0, 1]
    ];
    const isValidPos = (i, j) => {
        return i >= 0 && j >= 0 && i < m && j < n;
    };

    const isBoundary = (x, y) => {
        for (let [dx, dy] of positions) {
            if ((x === 0 || x === m-1 || y === 0 || y===n-1) && grid[x][y] === target || isValidPos(x + dx, y + dy) && grid[x + dx][y + dy] !== target) {
                return true;
            }
        }
        return false;
    };

    const bs = [];
    const visited = new Array(m);
    for (let i = 0; i < m; i++) {
        visited[i] = new Array(n).fill(0);
    }
    while (q.length) {
        const [r, c] = q.shift();
        if (isBoundary(r, c)) {
            bs.push([r, c]);
        }
        for (let [dx, dy] of positions) {
            if (isValidPos(r + dx, c + dy) && grid[r+dx][c+dy] === target && !visited[r+dx][c+dy]) {
                q.push([r + dx, c + dy]);
                visited[r+dx][c+dy] = true;
            }
        }
    }
    bs.forEach(([x, y]) => {
        grid[x][y] = color;
    });
    return grid;
};

733. 图像渲染

难度简单213收藏分享切换为英文接收动态反馈
有一幅以二维整数数组表示的图画，每一个整数表示该图画的像素值大小，数值在 0 到 65535 之间。
给你一个坐标 (sr, sc) 表示图像渲染开始的像素值（行 ，列）和一个新的颜色值 newColor，让你重新上色这幅图像。
为了完成上色工作，从初始坐标开始，记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。
最后返回经过上色渲染后的图像。
示例 1:
输入: image = [[1,1,1],[1,1,0],[1,0,1]] sr = 1, sc = 1, newColor = 2
输出: [[2,2,2],[2,2,0],[2,0,1]]
解析: 在图像的正中间，(坐标(sr,sc)=(1,1)), 在路径上所有符合条件的像素点的颜色都被更改成2。 注意，右下角的像素没有更改为2， 因为它不是在上下左右四个方向上与初始点相连的像素点。
注意:

• image 和 image[0] 的长度在范围 [1, 50] 内。
• 给出的初始点将满足 0 <= sr < image.length 和 0 <= sc < image[0].length。
• image[i][j] 和 newColor 表示的颜色值在范围 [0, 65535]内。

/**
 * @param {number[][]} image
 * @param {number} sr
 * @param {number} sc
 * @param {number} newColor
 * @return {number[][]}
 */
var floodFill = function(image, sr, sc, newColor) {
    const m = image.length;
    const n = image[0].length;

    const target = image[sr][sc];
    const q = [[sr, sc]];

    const positions = [
        [-1, 0], [1, 0], [0, -1], [0, 1]
    ];
    const isValidPos = (i, j) => {
        return i >= 0 && j >= 0 && i < m && j < n;
    };

    const isBoundary = (x, y) => {
        for (let [dx, dy] of positions) {
            if ((x === 0 || x === m-1 || y === 0 || y===n-1) && image[x][y] === target || isValidPos(x + dx, y + dy) && image[x + dx][y + dy] !== target) {
                return true;
            }
        }
        return false;
    };

    const bs = [];
    const visited = new Array(m);
    for (let i = 0; i < m; i++) {
        visited[i] = new Array(n).fill(0);
    }
    while (q.length) {
        const [r, c] = q.shift();
        bs.push([r, c]);
        for (let [dx, dy] of positions) {
            if (isValidPos(r + dx, c + dy) && image[r+dx][c+dy] === target && !visited[r+dx][c+dy]) {
                q.push([r + dx, c + dy]);
                visited[r+dx][c+dy] = true;
            }
        }
    }
    bs.forEach(([x, y]) => {
        image[x][y] = newColor;
    });
    return image;
};

剑指 Offer 13. 机器人的运动范围

难度中等341收藏分享切换为英文接收动态反馈
地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：
输入：m = 2, n = 3, k = 1 输出：3
示例 2：
输入：m = 3, n = 1, k = 0 输出：1
提示：

• 1 <= n,m <= 100
• 0 <= k <= 20

/**
 * @param {number} m
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var movingCount = function(m, n, k) {
  const q = [[0,0]];
  const maxLen = Math.max(m, n);
  const sum = (x) => {
    if (x < 10) {
      return x;
    }
    return (x % 10) + sum( Math.floor(x / 10));
  };
  const sums = new Array(maxLen);
  for (let i = 0; i < maxLen; i++) {
    sums[i] = sum(i);
  }

  const canReach = (x, y) => {
    return (sums[x] + sums[y]) <= k;
  };

  const positions = [
    [-1, 0], [1, 0], [0, -1], [0, 1]
  ];
  const isValidPos = (x, y) => {
    return x >=0 && y >= 0 && x < m && y < n;
  };
  let count = 0;
  const visited = new Array(m);
  for (let i = 0; i < m; i++) {
    visited[i] = new Array(n).fill(false);
  }
  visited[0][0] = true;
  while (q.length) {
    const [x, y] = q.shift();
    if (canReach(x, y)) {
      count += 1;
      for (let [dx, dy] of positions) {
        if (isValidPos(x + dx, y + dy) && !visited[x+dx][y+dy]) {
          visited[x+dx][y+dy] = true;
          q.push([x+dx, y+dy]);
        }
      }
    }
  }
  return count;
};

909. 蛇梯棋

难度中等82收藏分享切换为英文接收动态反馈
N x N 的棋盘 board 上，按从 1 到 NN 的数字给方格编号，编号* 从左下角开始，每一行交替方向。
例如，一块 6 x 6 大小的棋盘，编号如下：

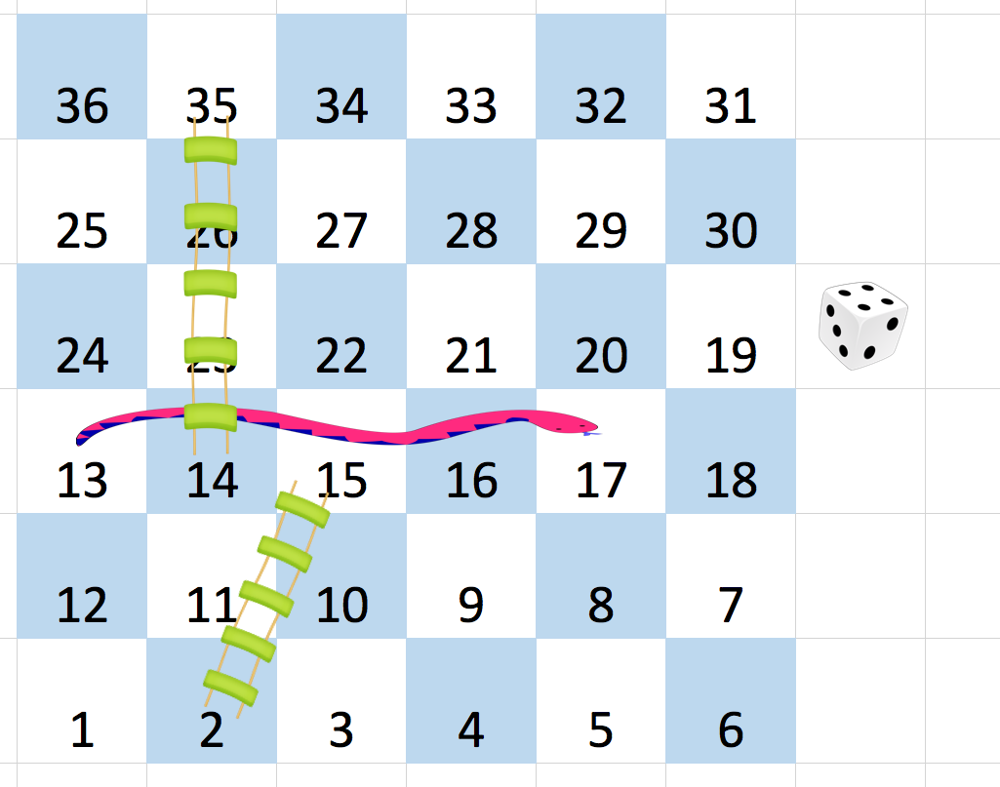
r 行 c 列的棋盘，按前述方法编号，棋盘格中可能存在 “蛇” 或 “梯子”；如果 board[r][c] != -1，那个蛇或梯子的目的地将会是 board[r][c]。
玩家从棋盘上的方格 1 （总是在最后一行、第一列）开始出发。
每一回合，玩家需要从当前方格 x 开始出发，按下述要求前进：

• 选定目标方格：从编号为 x+1，x+2，x+3，x+4，x+5，或者 x+6 的方格中选出一个作为目标方格 s ，目标方格的编号 <= N*N。
  • 该选择模拟了掷骰子的情景，无论棋盘大小如何，你的目的地范围也只能处于区间 [x+1, x+6] 之间。
• 传送玩家：如果目标方格 S 处存在蛇或梯子，那么玩家会传送到蛇或梯子的目的地。否则，玩家传送到目标方格 S 。

注意，玩家在每回合的前进过程中最多只能爬过蛇或梯子一次：就算目的地是另一条蛇或梯子的起点，你也不会继续移动。
返回达到方格 N*N 所需的最少移动次数，如果不可能，则返回 -1。

示例：
输入：[ [-1,-1,-1,-1,-1,-1], [-1,-1,-1,-1,-1,-1], [-1,-1,-1,-1,-1,-1], [-1,35,-1,-1,13,-1], [-1,-1,-1,-1,-1,-1], [-1,15,-1,-1,-1,-1]]
输出：4
解释： 首先，从方格 1 [第 5 行，第 0 列] 开始。
你决定移动到方格 2，并必须爬过梯子移动到到方格 15。
然后你决定移动到方格 17 [第 3 行，第 4 列]，必须爬过蛇到方格 13。
然后你决定移动到方格 14，且必须通过梯子移动到方格 35。
然后你决定移动到方格 36, 游戏结束。
可以证明你需要至少 4 次移动才能到达第 N*N 个方格，所以答案是 4。

提示：

• 2 <= board.length = board[0].length <= 20
• board[i][j] 介于 1 和 N*N 之间或者等于 -1。
• 编号为 1 的方格上没有蛇或梯子。
• 编号为 N*N 的方格上没有蛇或梯子。

/**
 * @param {number[][]} board
 * @return {number}
 */
var snakesAndLadders = function (board) {
    const m = board.length;
    const len = m * m;
    const dist = new Array(len + 1).fill(-1);
    dist[1] = 0;
    const getVal = (i) => {
        const rowno = Math.ceil(i / m);
        const x = m - rowno;
        const y = (rowno % 2 === 0 ? (m - 1 - (i - 1) % m) : ((i - 1) % m)) % m;
        return board[x][y];
    };

    const q = [1];
    while (q.length) {
        const i = q.shift();
        if (i === len) {
            break;
        }
        for (let j = i + 1; j <= Math.min(i + 6, len); j++) {
            const val = getVal(j);
            const next = val === -1 ? j : val;
            if (dist[next] === -1) {
                dist[next] = dist[i] + 1;
                q.push(next);
            }
        }
    }
    return dist[len];
};

279. 完全平方数

难度中等1067收藏分享切换为英文接收动态反馈
给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：
输入：n = 12 输出：3 解释：12 = 4 + 4 + 4

示例 2：
输入：n = 13 输出：2 解释：13 = 4 + 9
提示：

• 1 <= n <= 104

  /**
  * @param {number} n
  * @return {number}
  */
  var numSquares = function(n) {
  const up = Math.ceil(Math.sqrt(n));
  const numberSet = [];
  const dp = new Array(n+1);
  dp.fill(Infinity);
  
  for (let i = 1,n=1; i <= up; i++, n = i**2) {
    numberSet.push(n);
    dp[n] = 1;
  }
  
  for (let i = 1; i <= n; i++) {
    // if (numberSet.includes(i)) {
    //   dp[i] = 1;
    // } else {
      for (let k of numberSet) {
        if (i < k) {
          break;
        }
        dp[i] = Math.min(dp[i], dp[i-k] + 1);
      }
    // }
  }
  // console.log(dp.map((item , index) => `[${index}: ${item}]`).join(','));
  return dp[n];
  };