二分法 - 《算法》

二分答案

二分答案

875. 爱吃香蕉的珂珂

难度中等191收藏分享切换为英文接收动态反馈
珂珂喜欢吃香蕉。这里有 N 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。
珂珂可以决定她吃香蕉的速度 K （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 K 根。如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）。

示例 1：
输入: piles = [3,6,7,11], H = 8
输出: 4

示例 2：
输入: piles = [30,11,23,4,20], H = 5
输出: 30

示例 3：
输入: piles = [30,11,23,4,20], H = 6
输出: 23

提示：

1 <= piles.length <= 10^4
piles.length <= H <= 10^9

1 <= piles[i] <= 10^9

/**
* @param {number[]} piles
* @param {number} h
* @return {number}
*/
var minEatingSpeed = function(piles, h) {
// 由于每堆的时间消耗都是向上取整，故与总时间长度与堆的大小顺序无关
// 我们先排序，方便搜索解的大小。
piles.sort((a, b) => a-b);
const getTime = (p) => {
  let sum =0;
  for (let i = 0; i < piles.length; i++) {
    sum += Math.ceil(piles[i]/p);
  }
  return sum;
};
// 下限：每个小时1根
// 上限：最大堆的大小/小时
// 则在这个上下界的范围内采用二分查找方式获取满足条件的最小的速度。
let left = 1, right = piles[piles.length - 1], min = right;
// [left, right]是闭区间
while (left <= right) {
  let mid = left + ((right - left) >>> 1);
  let t = getTime(mid);
  if (t > h) {
    // 时间超过期望值，说明速度慢，left调整。
    left = mid + 1;
  } else {
    // 时间不超过期望值，说明速度快，right调整。
    right = mid - 1;
    // 更新结果大小，求的是最小速度，故取min。
    min = Math.min(min, mid);
  }
}
return min;
};

719. 找出第 k 小的距离对

给定一个整数数组，返回所有数对之间的第 k 个最小距离。一对 (A, B) 的距离被定义为 A 和 B 之间的绝对差值。
示例 1:
输入：
nums = [1,3,1]
k = 1
输出：0
解释：
所有数对如下：
(1,3) -> 2
(1,1) -> 0
(3,1) -> 2
因此第 1 个最小距离的数对是 (1,1)，它们之间的距离为 0。

提示:

2 <= len(nums) <= 10000.
0 <= nums[i] < 1000000.
1 <= k <= len(nums) * (len(nums) - 1) / 2.

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var smallestDistancePair = function(nums, k) {
  // 在全组合中寻找，故先排序
  nums.sort((a, b) => a-b);
  // 下界： 0，两个数字相同。
  // 上界：最大-最小
  let left = 0, right = nums[nums.length - 1] - nums[0];
  // 枚举所有的距离
  while (left < right) {
    let mid = (left + right) >>> 1;
    // 计数mid距离的组合数量。
    let count = 0, i = 0;
    // 数组已经排序，故滑动窗口扫描。
    // i: 左指针
    // j: 右指针
    for (let j = 0; j < nums.length; j++) {
      // 窗口不满足条件，左边界移动
      while (nums[j] - nums[i] > mid) {
        i++;
      }
      count += j - i;
    }

    // 计数比K小，下界向上调整提升
    if (count < k) {
      left = mid + 1;
    } else {
      // 上界向下调整
      right = mid;
    }
  }
  return left;
};

【MEDIUM】寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。
假设 nums 只有一个重复的整数，找出这个重复的数。
你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。
示例 1：
输入： nums = [1,3,4,2,2] 输出： 2<br />示例 2： <br />输入： nums = [3,1,3,4,2] 输出： 3
示例 3：
输入： nums = [1,1] 输出： 1<br />示例 4： <br />输入： nums = [1,1,2] 输出： 1
提示：

1 <= n <= 105
nums.length == n + 1
1 <= nums[i] <= n
nums 中只有一个整数出现两次或多次，其余整数均只出现一次

进阶：

如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？ ```javascript // 解法一：快慢指针 /**
- @param {number[]} nums
- @return {number} */ var findDuplicate = function(nums) { let r = 0, l = 0; do { l = nums[l]; r = nums[nums[r]]; } while (l !== r); l = 0; while (l !== r) { l = nums[l]; r = nums[r]; } return l; };

// 解法二：二分答案，计数小于目标的个数，这个个数的函数f(x)具有单调性 /**

@param {number[]} nums
@return {number} */ var findDuplicate = function(nums) { let l = 0, r = nums.length-1, ans = Number.MAX_SAFE_INTEGER; while (l <= r) { let m = l + ((r - l) >>> 1); let t = 0; for (let i = 0; i < nums.length; i++) { if (nums[i] <= m) {
```
 t += 1;
```
} } if (t <= m) { l = m + 1; } else { r = m - 1; ans = Math.min(ans, m); } } return ans; }; ```

410. 分割数组的最大值
难度困难543收藏分享切换为英文接收动态反馈
给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。
设计一个算法使得这 m 个子数组各自和的最大值最小。

示例 1：
输入：nums = [7,2,5,10,8], m = 2
输出：18
解释： 一共有四种方法将 nums 分割为 2 个子数组。其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。
示例 2：
输入：nums = [1,2,3,4,5], m = 2
输出：9
示例 3：
输入：nums = [1,4,4], m = 3
输出：4

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 106
1 <= m <= min(50, nums.length) ```javascript /**
- @param {number[]} nums
- @param {number} m
- @return {number} */ var splitArray = function(nums, m) { const sum = .reduce(nums, (r, v) => r += v, 0); let l = .max(nums), r = sum; while (l <= r) { // sum和 let mid = l + ((r - l) >>> 1); let t = 0; s = -1;
  
  // 统计连续子数组个数，使得数组之和<= mid for (let i = 0; i < nums.length; i++) { s = s === -1 ? nums[i] : (s + nums[i]); if (s > mid) {
```
s = -1;
s = nums[i];
t++;
```
  } } if (s != -1 && s !== 0) { t++; }
  
  // 比m大，说明分组分多了，要向右移动左边界。 if (t > m) { l = mid + 1; } else { // 否则，向左边界靠齐。 r = mid - 1; } } return l; };

<a name="nuaEt"></a>
### 数值二分
<a name="WeEmd"></a>
#### [34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/)
难度中等1148<br />给定一个按照升序排列的整数数组 `nums`，和一个目标值 `target`。找出给定目标值在数组中的开始位置和结束位置。<br />如果数组中不存在目标值 `target`，返回 `[-1, -1]`。<br />**进阶：**

- 你可以设计并实现时间复杂度为 `O(log n)` 的算法解决此问题吗？

 <br />**示例 1：**<br />**输入：**nums = [`5,7,7,8,8,10]`, target = 8<br />**输出：**[3,4]<br />**示例 2：**<br />**输入：**nums = [`5,7,7,8,8,10]`, target = 6<br />**输出：**[-1,-1]<br />**示例 3：**<br />**输入：**nums = [], target = 0<br />**输出：**[-1,-1]<br /> <br />**提示：**

- `0 <= nums.length <= 105`
- `-109 <= nums[i] <= 109`
- `nums` 是一个非递减数组
- `-109 <= target <= 109`

```javascript
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var searchRange = function(nums, target) {
  let left = 0, right = nums.length - 1;
  let ans = [-1, -1];
  // find lower bound.
  while (left + 1 < right) {
    let mid = left + ((right - left) >>> 1);
    if (nums[mid] >= target) {
      right = mid;
    } else {
      left = mid + 1;
    }
  }
  if (nums[right] === target) {
    ans[0] = right;
  }
  if (nums[left] === target) {
    ans[0] = left;
  }
  left = 0;
  right = nums.length - 1;
  // find upper bound
  while (left + 1 < right) {
    let mid = left + ((right - left) >>> 1);
    if (nums[mid] <= target) {
      left = mid;
    } else {
      right = mid - 1;
    }
  }
  if (nums[left] === target) {
    ans[1] = left;
  }
  if (nums[right] === target) {
    ans[1] = right;
  }
  return ans;
};

162. 寻找峰值

难度中等490
峰值元素是指其值大于左右相邻值的元素。
给你一个输入数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。

示例 1：
输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。
示例 2：
输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5
解释：你的函数可以返回索引 1，其峰值元素为 2；
或者返回索引 5，其峰值元素为 6。

提示：

1 <= nums.length <= 1000
-231 <= nums[i] <= 231 - 1
对于所有有效的 i 都有 nums[i] != nums[i + 1]

进阶：你可以实现时间复杂度为 O(logN) 的解决方案吗？

/**
 * @param {number[]} nums
 * @return {number}
 */
var findPeakElement = function(nums) {
  let left = 0, right = nums.length - 1;
  while (left < right) {
    let mid = left + ((right - left) >>> 1);
    // 比后面的大，则丢弃右侧，向左寻找
    if (nums[mid] > nums[mid + 1]) {
      right = mid;
    } else {
    // 不大于后面，丢弃左侧，向右寻找
      left = mid + 1;
    }
  }
  return left;
};

270. 最接近的二叉搜索树值

难度简单86
给定一个不为空的二叉搜索树和一个目标值 target，请在该二叉搜索树中找到最接近目标值 target 的数值。
注意：

给定的目标值 target 是一个浮点数
题目保证在该二叉搜索树中只会存在一个最接近目标值的数

示例：
输入: root = [4,2,5,1,3]，目标值 target = 3.714286

4<br />   / \<br />  2   5<br /> / \<br />1   3

输出: 4

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} target
 * @return {number}
 */
var closestValue = function(root, target) {
  let minDiff = Number.MAX_SAFE_INTEGER, ans = Number.MAX_SAFE_INTEGER;
  const dfs = (node, t) => {
    const diff = Math.abs(node.val - t);
    if (diff < minDiff) {
      minDiff = diff;
      ans = node.val;
    }
    if (node.val > t && node.left) {
      dfs(node.left, t);
    } else if (node.val < t && node.right) {
      dfs(node.right, t);
    }
  };
  dfs(root, target);
  return ans;
};

50. Pow(x, n)

难度中等709
实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。

示例 1：
输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：
输入：x = 2.10000, n = 3
输出：9.26100

示例 3：
输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1

-104 <= xn <= 104

/**
* @param {number} x
* @param {number} n
* @return {number}
*/
var myPow = function (x, n) {
const st = [[1, 0], [x, 1]];
const calc = (b) => {
  if (b === 0) return 1;
  let t = 1; count = 1;
  while (t * 2 < b) {
    t = t * 2;
    count++;
  }
  while (!st[count]) {
    let [top, idx] = st[st.length - 1];
    st.push([top * top, idx + 1]);
  }
  return st[count][0] * calc(b - t);
};
return n >= 0 ? calc(n) : 1/calc(-n);
};

4. 寻找两个正序数组的中位数

难度困难4445收藏分享切换为英文接收动态反馈
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例 1：
输入：nums1 = [1,3], nums2 = [2] 输出：2.00000 解释：合并数组 = [1,2,3] ，中位数 2
示例 2：
输入：nums1 = [1,2], nums2 = [3,4] 输出：2.50000 解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
示例 3：
输入：nums1 = [0,0], nums2 = [0,0] 输出：0.00000
示例 4：
输入：nums1 = [], nums2 = [1] 输出：1.00000
示例 5：
输入：nums1 = [2], nums2 = [] 输出：2.00000

提示：

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function(nums1, nums2) {
  let nl = nums1.length + nums2.length;
  let k = Math.floor((nl + 1)/2);
  if (nums1.length > nums2.length) return findMedianSortedArrays(nums2, nums1);
  const getK = (k) => {
    let l = 0, r = 0;
    while (k>0) {
      if (l >= nums1.length) return nums2[r + k - 1];
      if (r >= nums2.length) return nums1[l + k - 1];
      if (k === 1) return Math.min(nums1[l], nums2[r]);

      let nextk = k >>> 1;
      let lm = l + nextk - 1 >= nums1.length ? Number.MAX_SAFE_INTEGER : nums1[l + nextk - 1];
      let rm = r + nextk- 1 >= nums2.length ? Number.MAX_SAFE_INTEGER : nums2[r + nextk - 1];
      if (lm <= rm) {
        l += nextk;
      } else {
        r += nextk;
      }
      k -= nextk;
    }
  };

  if (nl % 2 === 0) {
    return (getK(k) + getK(1 + k))/2;
  }
  return getK(k);
};

74. 搜索二维矩阵

难度中等498收藏分享切换为英文接收动态反馈
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

示例 1：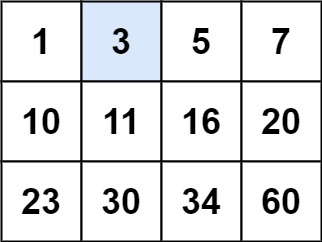

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：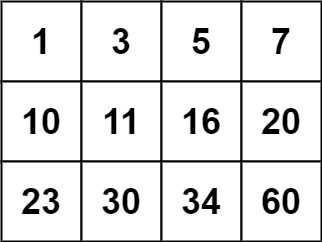

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function(matrix, target) {
  let m = matrix.length;
  let n = matrix[0].length;
  let l = 0;
  let r = m * n;
  while (l < r) {
    let mid = l + ((r - l) >>> 1);
    let col = mid % n;
    let row = Math.floor(mid / n);
    let num = matrix[row][col];
    if (num === target) {
      return true;
    } else if (num > target) {
      r = mid;
    } else if (num < target) {
      l = mid + 1;
    }
  }
  return false;
};