- 题目类型一: 单调状态判断
- 题目类型二:下一个更大的元素
- 变种一:求下标差值:每日温度
- 链接">变种二:下一个更大元素二(循环数组)链接
- 链接">变种三:【无形单调栈】下一个更大的元素三 链接
- 链接">题目类型三:树 链接
题目类型一: 单调状态判断
132模式 https://leetcode-cn.com/problems/132-pattern
给你一个整数数组 nums ,数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成,并同时满足:i < j < k 和 nums[i] < nums[k] < nums[j] 。
如果 nums 中存在 132 模式的子序列 ,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [1,2,3,4]
输出:false
解释:序列中不存在 132 模式的子序列。
示例 2:
输入:nums = [3,1,4,2]
输出:true
解释:序列中有 1 个 132 模式的子序列: [1, 4, 2] 。
示例 3:
输入:nums = [-1,3,2,0]
输出:true
解释:序列中有 3 个 132 模式的的子序列:[-1, 3, 2]、[-1, 3, 0] 和 [-1, 2, 0] 。
提示:
- n == nums.length
- 1 <= n <= 2 * 105
- -109 <= nums[i] <= 109
题解:
/*** @param {number[]} nums* @return {boolean}*/var find132pattern = function(nums) {const st = [];let last = -1; // 代表 132 中的 2的元素下标。// 采用从后向前的单调递减栈, 132 模式,对应i1 < i2 < i3. 整体 1 < 2 为单调递减,3 > 2为不满足单调性被弹出的元素// 故后续只要判断1 < 3 则表示找到这样的元素对。for (let i = nums.length - 1; i >= 0; i--) {// 退出条件:新的1 比 2小,则满足返回条件。if (last !== -1 && nums[i] < nums[last]) {return true;}// 单调性保持// 单调递减(栈中元素的大小关系,非出栈时的大小关系),则新元素在比当前栈顶元素大的时候,// 不断的弹出栈中的元素,直到栈顶元素小于新元素或者栈为空。// 在这里即为保持单调性3(i,入栈后的新栈顶) < 2(st[st.length-1],旧栈顶)// 因此检测条件取反时可以将栈中不满足单调性的旧的栈顶元素全部弹出。// 用last保存最后弹出的那个栈顶。while (st.length && nums[st[st.length - 1]] < nums[i]) {const t = st.pop();last = t;}st.push(i); // 入栈新栈顶。}return false;};
题目二: 剑指 Offer 33. 二叉搜索树的后序遍历序列 链接
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5<br /> / \<br /> 2 6<br /> / \<br /> 1 3<br />示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
提示:
数组长度 <= 1000
/**
* @param {number[]} postorder
* @return {boolean}
*/
var verifyPostorder = function(postorder) {
const st = [];
let r = -1; // 状态变量,保存右子节点
for(let i = postorder.length - 1; i >= 0; i--) {
// 退出条件:新的下标i的元素比r下标的元素大,则验证失败,返回false
if (r !== -1 && postorder[i] > postorder[r]) {
return false;
}
// 单调性维持:单调递增栈
// 每次更新 状态变量, 当退出while循环时,r即为 i下标对应的右子树节点。
while (st.length && postorder[st[st.length - 1]] > postorder[i]) {
r = st.pop();
}
st.push(i);
}
return true;
};
题目类型二:下一个更大的元素
下一个更大的元素:https://leetcode-cn.com/problems/next-greater-element-i
给你两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于 num1 中的数字 4 ,你无法在第二个数组中找到下一个更大的数字,因此输出 -1 。
对于 num1 中的数字 1 ,第二个数组中数字1右边的下一个较大数字是 3 。
对于 num1 中的数字 2 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
对于 num1 中的数字 2 ,第二个数组中的下一个较大数字是 3 。
对于 num1 中的数字 4 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
提示:
1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 104
nums1和nums2中所有整数 互不相同
nums1 中的所有整数同样出现在 nums2 中
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
var nextGreaterElement = function(nums1, nums2) {
const mp = new Map();
const st = [];
for (let i = 0; i < nums2.length; i++) {
// 单调性维持:单调递减栈,
while (st.length && nums2[st[st.length-1]] < nums2[i]) {
const t = st.pop();
// 更新存在的元素的位置下标,只保留结果集中需要的。
mp.set(nums2[t], i);
}
st.push(i);
}
// 将下标数组进行结果转换。
return nums1.map(i => {
if (mp.has(i)) {
return nums2[mp.get(i)];
}
return -1;
});
};
变种一:求下标差值:每日温度
剑指 Offer II 038. 每日温度 https://leetcode-cn.com/problems/iIQa4I
739 题 每日温度: https://leetcode-cn.com/problems/daily-temperatures/
请根据每日 气温 列表 temperatures ,重新生成一个列表,要求其对应位置的输出为:要想观测到更高的气温,至少需要等待的天数。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
提示:
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100
/**
* @param {number[]} temperatures
* @return {number[]}
*/
var dailyTemperatures = function(temperatures) {
// 单调差值数组定义,默认填0
const ans = new Array(temperatures.length).fill(0);
const st = [];
for (let i = 0; i < temperatures.length; i++) {
// 单调递减保持,弹出的每个下标都是不满足单调递减性,用当前下标与栈顶下标的差值填充返回结果。
while (st.length && temperatures[st[st.length - 1]] < temperatures[i]) {
const t = st.pop();
// 与上例相比多了一个结果状态更新,弹出的时候知道谁把元素弹出了,所以在这个时候来更新。
// 由于是返回差值天数,故计算两者的下标差值
ans[t] = i - t;
}
// 新栈顶
st.push(i);
}
return ans;
};
变种二:下一个更大元素二(循环数组)链接
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
注意: 输入数组的长度不会超过 10000。
/**
* @param {number[]} nums
* @return {number[]}
*/
var nextGreaterElements = function(nums) {
const ans = new Array(nums.length).fill(-1);
let st = [], loop = nums.length << 1;
// 循环数组,所以循环的条件就是2倍的数组长度。
for (let i = 0; i < loop; i++) {
// 由于是循环数组,所以结果的保存所用下标要重新计算,用长度取模即可。
const vi = i % nums.length;
// 单调性维持:单调递减栈,不停的弹出比新元素小的的元素,并更新结果。
while (st.length && nums[st[st.length-1]] < nums[vi]) {
const t = st.pop();
// 结果更新
ans[t] = nums[vi];
}
st.push(vi);
}
return ans;
};
变种三:【无形单调栈】下一个更大的元素三 链接
给你一个正整数 n ,请你找出符合条件的最小整数,其由重新排列 n 中存在的每位数字组成,并且其值大于 n 。如果不存在这样的正整数,则返回 -1 。
注意 ,返回的整数应当是一个 32 位整数 ,如果存在满足题意的答案,但不是 32 位整数 ,同样返回 -1 。
示例 1:
输入:n = 12
输出:21
示例 2:
输入:n = 21
输出:-1
提示:
1 <= n <= 231 - 1
/**
* @param {number} n
* @return {number}
*/
var nextGreaterElement = function(n) {
if (n < 12) {
return -1;
}
const ns = [];
let v = n;
while (v) {
let last= v % 10;
ns.unshift(last);
v -= last;
v /= 10;
}
const swap = (i, j) => {
[ns[i], ns[j]] = [ns[j], ns[i]];
};
const max = Math.pow(2, 31) - 1;
for (let i = ns.length - 1; i >= 0; i--) {
// 找到第一个比前面大的元素
// 单调性维持,从后面向前是为单调递增栈,前面的元素要比后面的大,不满足,说明找到了需要变化的最高位数。
// 由于只是需要寻找位置,所以不需要O(n)的栈空间来做栈操作。
if (i < ns.length-1 && ns[i] < ns[i+1]) {
// 由于是单调递增栈,从后面向前面寻找第一个大于i的元素,并交换两个,然后排序i+1后面的元素。
for (let j = ns.length - 1; j >= i + 1; j--) {
if (ns[j] > ns[i]) {
swap(i, j);
// 思路一:TODO: 抽象一个inplace的区间排序操作。
const sorted = ns.slice(i+1).sort((a, b) => a-b);
const ans = Number([...ns.slice(0, i+1), ...sorted].join(''));
// 思路二: 由于i+1后面的元素已经是降序的,故直接首尾交换这个区间中的元素也可以实现排序。
for (let m = i+1, n = ns.length - 1; m < n; m++,n--) {
swap(m, n);
}
const ans = Number(ns.join(''));
// 边界条件,不能比32位整数大。
return (ans <= max) ? ans : -1;
}
}
}
}
return -1;
};
题目类型三:树 链接
给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下:
二叉树的根是数组 nums 中的最大元素。
左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。
返回有给定数组 nums 构建的 最大二叉树 。
示例 1:
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示: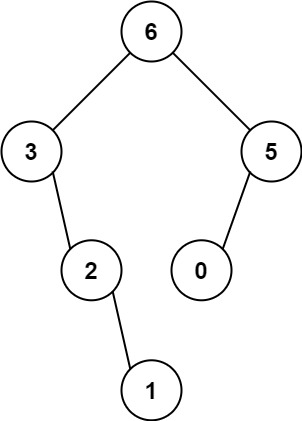
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
示例 2: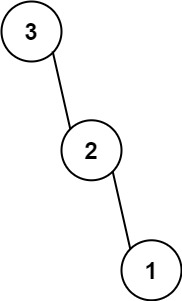
输入:nums = [3,2,1]
输出:[3,null,2,null,1]
提示:
1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同
解法一:递归
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} nums
* @return {TreeNode}
*/
var constructMaximumBinaryTree = function(nums) {
const dfs = (arr, left, right) => {
// 查找区间内最大值的位置,
let max = -1;
for (let i = left; i <= right; i++) {
if (max === -1 || nums[max] < nums[i]) {
max = i;
}
}
if (max !== -1) {
// 递归构造左右子节点
return new TreeNode(nums[max], dfs(arr, left, max - 1), dfs(arr, max + 1, right));
}
return null;
}
return dfs(nums, 0, nums.length - 1);
};
解法二:单调递减栈(栈顶最大元素)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} nums
* @return {TreeNode}
*/
var constructMaximumBinaryTree = function(nums) {
const st = new Array();
for (let i = 0; i < nums.length; i++) {
const node = new TreeNode(nums[i]);
// 单调性维持,单调递减栈,不满足,则进行弹出处理。
while (st.length && st[st.length - 1].val < nums[i]) {
const t = st.pop();
// 弹出处理,若当前栈顶比i下标元素小,则说明弹出节点为栈顶元素的右子节点。
// 若栈空,则弹出元素为i下标元素的左子节点,因为栈中元素都是在i的左侧。
if (st.length && st[st.length - 1].val < nums[i]) {
st[st.length-1].right = t;
} else {
node.left = t;
}
}
st.push(node);
}
// 栈中遗留元素的处理逻辑:
// 后一个元素是前一个的右子节点,栈中元素的先后顺序没有该表,后一个元素在原数组中也是在前一个元素的右侧。
let t = st.pop();
while (st.length) {
st[st.length - 1].right = t;
t = st.pop();
}
return t;
};

