题目一：路径寻找
- 变种一：返回结果集
- 437. 路径总和 III">变种二：437. 路径总和 III
题目二：子节点大小选择
- 111. 二叉树的最小深度">111. 二叉树的最小深度
题目类型三：有序性

题目一：路径寻找

112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。

叶子节点是指没有子节点的节点。

示例 1：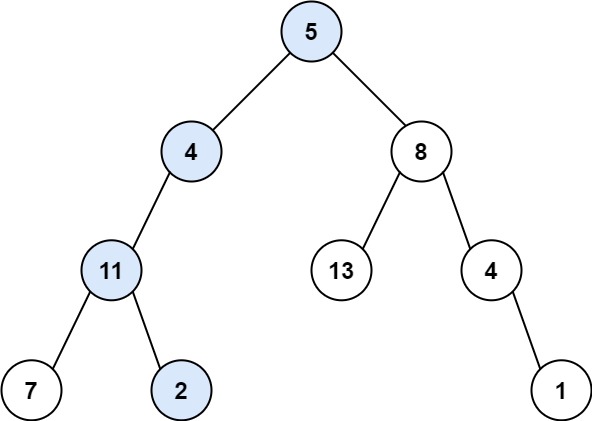
二叉树 - 图1
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true

示例 2：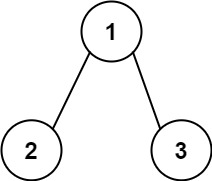
二叉树 - 图2
输入：root = [1,2,3], targetSum = 5
输出：false

示例 3：
输入：root = [1,2], targetSum = 0
输出：false

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/path-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function(root, targetSum) {
  const dfs = (node, t) => {
    // 叶子节点，满足条件t === node.val
    if (node && t === node.val && (!node.left && !node.right)) {
      return true;
    }
    if (node && dfs(node.left, t - node.val)) return true;
    if (node && dfs(node.right, t - node.val)) return true;
    return false;
  };
  return dfs(root, targetSum);
};

变种一：返回结果集

路径总和 II https://leetcode-cn.com/problems/path-sum-ii

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。

叶子节点是指没有子节点的节点。

示例 1：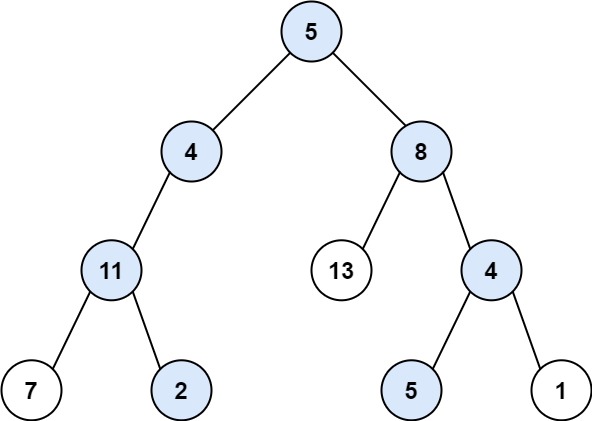
二叉树 - 图3
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：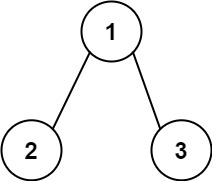
二叉树 - 图4
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：
输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/path-sum-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number[][]}
 */
var pathSum = function(root, targetSum) {
  const ans = [];
  const dfs = (node, t, paths) => {
    // 叶子节点，满足条件t === node.val
    if (node && t === node.val && (!node.left && !node.right)) {
      paths.push(node.val);
      // 复制到结果集合中
      ans.push([...paths]);
      paths.pop();
      return true;
    }
    if (node) {
      // 与前一的差异是需要回溯，在左右两个子节点间遍历，因为是返回所有结果结果集。
      paths.push(node.val);
      dfs(node.left, t - node.val, paths);
      dfs(node.right, t - node.val, paths);
      // 回溯堆栈
      paths.pop();
    }
    return false;
  };
  dfs(root, targetSum, []);
  return ans;
};

变种二：437. 路径总和 III

难度中等940收藏分享切换为英文接收动态反馈
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。
路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：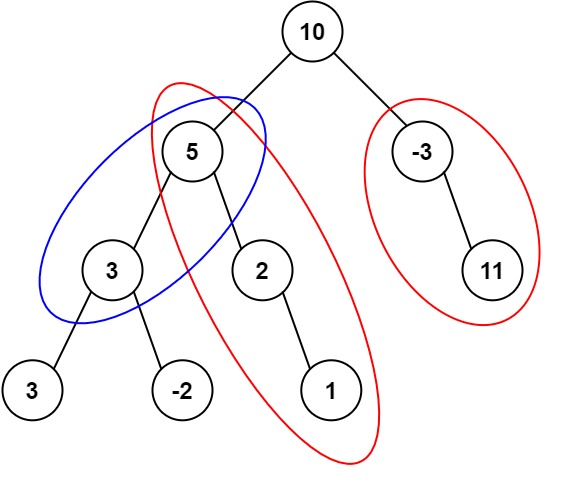
二叉树 - 图5
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109
-1000 <= targetSum <= 1000

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function(root, targetSum) {
  if (!root) return 0;
  let ans = 0;
  const dfs = (node, t) => {
    if (!node) return;
    // 叶子节点，满足条件t === node.val，不要return，继续寻找，有可能后续会右多个节点之和为0.
    if (t === node.val) {
      ans++;
    }
    dfs(node.left,  t - node.val);
    dfs(node.right,  t - node.val);
  };
  dfs(root, targetSum);
  // 再以左右子树来遍历寻找。
  ans += pathSum(root.left, targetSum);
  ans += pathSum(root.right, targetSum);
  return ans;
};

题目二：子节点大小选择

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。

示例 1：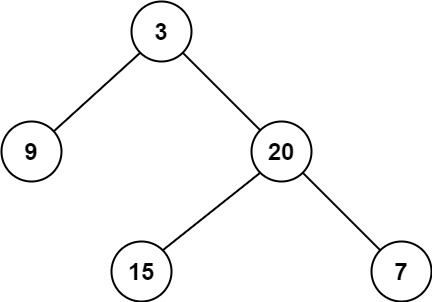
二叉树 - 图6
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 105] 内

-1000 <= Node.val <= 1000

/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
*     this.val = (val===undefined ? 0 : val)
*     this.left = (left===undefined ? null : left)
*     this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
const dfs = (node) => {
  if (!node) return 0;
  // 只有左子树，结果等 1 + h(left);
  if (node && !node.right) {
    return 1 + dfs(node.left);
  }
  // 只有右子树，结果等 1 + h(right);
  if (node && !node.left) {
    return 1 + dfs(node.right);
  }
  return Math.min(dfs(node.left), dfs(node.right)) + 1;
};
return dfs(root);
};

题目类型三：有序性

114. 二叉树展开为链表
难度中等878收藏分享切换为英文接收动态反馈
给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：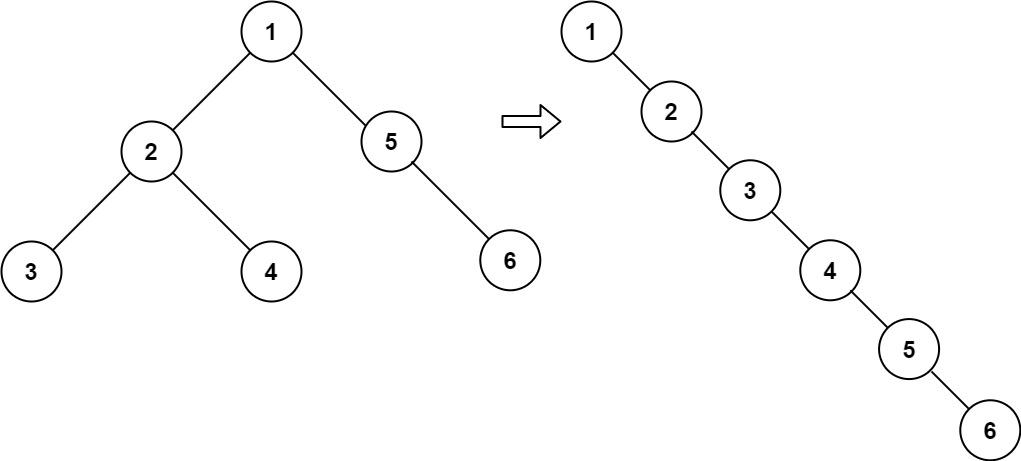

输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

解法一：递归

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
  let top; // 只使用栈顶指针
  const dfs = (node) => {
    if (!node) {
      return;
    }
    let left = node.left;
    let right = node.right;
    if (top) { 
      // 关联右指针
      top.right = node;
      top.left = null;
    }
    // 入栈
    top = node;
    dfs(left);
    dfs(right);
  };
  dfs(root);
  return root;
};

解法二：三指针

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
  let curr = root;
  while (curr !== null) {
    // 左子树不为空
    if (curr.left !== null) {
      const next = curr.left;
      // 找到当前节点的左子树的最右节点，这个节点为pre。
      let pre = next;
      while (pre.right !== null) {
        pre = pre.right;
      }
      // 移动cur的右子树为pre的右子树。
      pre.right = curr.right;
      // 旋转左子树为右子树。
      curr.left = null;
      curr.right = next;
    }
    // 只有右子树，则继续跳跃指针
    curr = curr.right;
  }
};

二叉树