组合数学
阶乘
n! = n (n - 1) (n - 2) …. 1
排列
从n个不同元素中,任取m(m≤n)个元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号p(n,m)表示.p(n,m)=n(n-1)(n-2)……(n-m+1)=(规定0!=1).
组合
从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数.用符号c(n,m)表示.c(n,m)=p(n,m)/m!=n!/((n-m)!*m!);c(n,m)=c(n,n-m);
组合数公式
二项式定理:
二项式系数符合: 杨辉三角
卡特兰数
定义式
-
组合数公式 (用生成函数推导定义式)
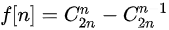
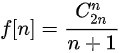
-
卡特兰数列
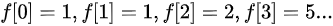
-
应用方向
括号匹配问题
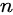 个左括号,
个左括号, 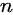 个右括号,对于每一个位置,左括号数大于等于右括号数的方案总数。
个右括号,对于每一个位置,左括号数大于等于右括号数的方案总数。- 等价于
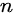 个
个 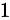 ,
, 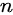 个
个 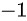 ,每个位置前缀和大于等于
,每个位置前缀和大于等于 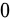 的方案总数。
的方案总数。 - 两种理解方向:
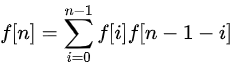 。枚举第一次前缀和为
。枚举第一次前缀和为 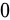 的位置,假如第
的位置,假如第 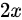 个点为第一次前缀和为
个点为第一次前缀和为 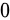 的点,则固定第一个数为
的点,则固定第一个数为 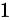 ,第
,第 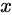 个数为
个数为 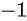 ,则对答案贡献为
,则对答案贡献为  。
。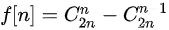 。总方案数为
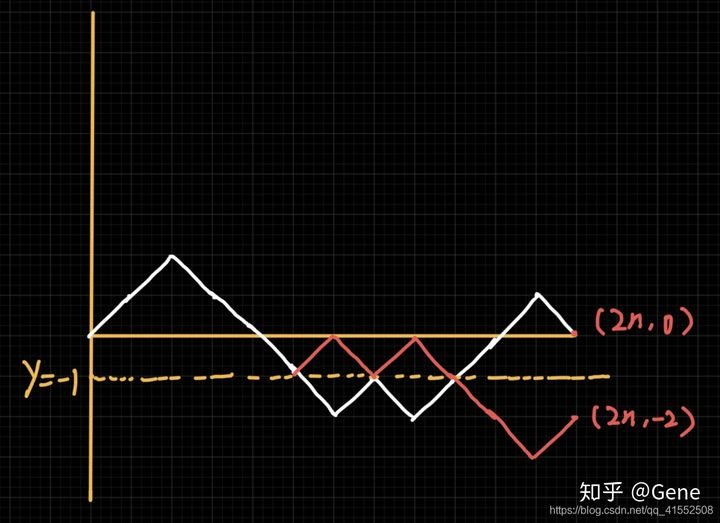
。总方案数为  ,现需求不符合条件的方案数,将问题转化为网格上的折线问题。第
,现需求不符合条件的方案数,将问题转化为网格上的折线问题。第 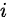 次在
次在 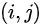 处,第
处,第 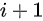 次在
次在 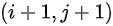 或
或 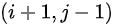 处,终点为
处,终点为  。不符合条件则说明折线上出现了
。不符合条件则说明折线上出现了 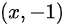 这个点,
这个点, 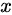 为第一次到达
为第一次到达 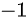 的点,我们将
的点,我们将 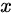 点之后的折线沿
点之后的折线沿 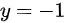 对称过来,则终点为
对称过来,则终点为 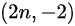 ,则一共有
,则一共有  个
个 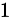 ,
, 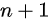 个
个 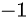 ,即不合法的方案总数为
,即不合法的方案总数为 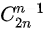 ,因此
,因此 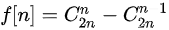 。
。
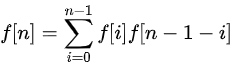
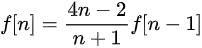
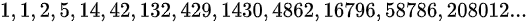
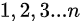 ,求有多少个不同的出栈序列。
,求有多少个不同的出栈序列。
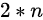 个点,将这些点对连接起来使得所得到的
个点,将这些点对连接起来使得所得到的 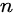 条线段不想交的方案数。
条线段不想交的方案数。
 个节点,能构成多少种形状不同的二叉树。
个节点,能构成多少种形状不同的二叉树。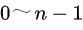 个点,右边则可以取
个点,右边则可以取 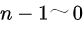 个点,相乘再累加即可得到答案。
个点,相乘再累加即可得到答案。
