综述

「滑动窗口」是一类通过使用两个变量在数组上同向交替移动解决问题的算法。这一类问题的思考路径通常是：先思考暴力解法，分析暴力解法的缺点（一般而言暴力解法的缺点是重复计算），然后 结合问题的特点，使用「双指针」技巧对暴力解法进行剪枝。因此，思考算法设计的合理性是更关键的，这一点适用于所有算法问题。

• left 和 right 同方向移动；
• 定义条件，即我们需要时刻检测的一件事情；
• 原理：充分利用本题本身的特点，以减少不必要的计算；
• 利用「循环不变量」保证代码边界正确；
• 不要记忆代码模板，应该结合具体问题分析出什么时候滑动窗口最长，什么时候滑动窗口最短；
• 掌握处理字符串的技巧。

最长连续

范式：求最长，则主循环以右边界为主，每次必然右移，然后在循环中判断是否满足窗口条件。
步骤：
1、初始时，l=r=0 定义窗口的区间为[l, r]
2、循环时，保持 r < len, 针对每个r，都将其加入到结果集计算过程中，保持窗口有效，持续增长长度，每右移一次右边界，判断一次是否有效窗口，若无效，右移左侧边界，直到窗口有效，则所得的结果即为当前的最长结果；
3、更新结果集
4、循环退出时，r = len

let l = 0, r = 0, ans = 结果集
while (r < |len|) {
   新入元素r，计算结果集;
   // 如果isWindow判断需要使用到r访问数组，则需要判断r是否已经越界。
   while (isWindow()) {
     右移左边界l，
   }
   r++;
   // 如果更新结果集需要使用到r，则需要判断r是否已经越界。
   更新结果集。
}
return ans;

剑指 Offer II 119. 最长连续序列

/**
 * @param {number[]} nums
 * @return {number}
 */
var longestConsecutive = function(nums) {
  if (nums.length < 2) return nums.length;
  nums.sort((a, b) => a - b);
  let left = 0, right = 0, ans = 1, dup = 0;
  while (right < nums.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    // !isValidWindow, 不需要使用while来遍历，不满足旧直接跳过所有中间状态，并将dup重置为0.
    if (right >= 1 && nums[right] - nums[right-1] > 1) {
      left = right;
      dup = 0;
    } else if (right >= 1 && nums[right] - nums[right-1] === 0) {
      // 当连续的数字相同时，计数，由于只是去子序列，所以相同的只需要一个就可以了（窗口内）。
      dup++;
    }
    // 这里是后加加，防止上面两个statement数组越界。
    right++; 
    // 由于已经++，计算长度的时候不需要再+1补充了。
    ans = Math.max(ans, right - left - dup);
  }
  return ans;
};

674. 最长连续递增序列

/**
 * @param {number[]} nums
 * @return {number}
 */
var findLengthOfLCIS = function(nums) {
  // init: [left, right) = [0, 1), 初始长度是ans = 1；
  // loop: [1, len) => right 的区间范围，如果比前一个小，则不满足单调性，left 直接跳到right的位置。
  // end: right = len
  let left = 0, right = 1, ans = right - left;
  while (right < nums.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    // 1、!isValidWindow, 不需要使用while来遍历，不满足直接跳过所有中间状态。
    if (nums[right-1] >= nums[right]) {
      left = right;
    }
    // isValidWindow， 右侧最右，左侧有效，即为最大窗口。
    right++;
    // update max value
    ans = Math.max(ans, right - left);
  }
  return ans;
};

1658. 将 x 减到 0 的最小操作数

/**
 * @param {number[]} nums
 * @param {number} x
 * @return {number}
 */
var minOperations = function(nums, x) {
  let sum = 0;
  for (let i = 0; i < nums.length; i++) {
    sum += nums[i];
  }
  // 将问题转换为最长数组和为sum-x
  let t = sum - x;
  if (t < 0) return -1;

  let l = 0, r = 0, s = 0, ans = Number.MIN_SAFE_INTEGER;
  while (r < nums.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    // 计算前缀和
    s += nums[r];

    // !isValidWindow，需要使用while，来缩减窗口到窗口合法。或者达到边界。
    while (l < nums.length && s > t) {
      s -= nums[l++];
    }
    // isValidWindow， 右侧最右，左侧有效，即为最大窗口。
    r++;
    // update result on condition，右侧最右，左侧有效，即为最大窗口。
    if (s === t) {
      ans = Math.max(ans, r - l);
    }
  }
  // 有条件才能获取值的时候，要判断是否为空的场景。
  return ans === Number.MIN_SAFE_INTEGER ? -1: nums.length - ans;
};

424. 替换后的最长重复字符

/**
 * @param {string} s
 * @param {number} k
 * @return {number}
 */
var characterReplacement = function(s, k) {
  let l = 0, r = 0, ct = new Array(26).fill(0), max = 0, ans = 0;

  // isValidWindow在r++之后使用，所以窗口为右开区间，长度为：r-l
  const isValidWindow = () => r - l + 1<= max + k;
  const get = (r) => s.charCodeAt(r) - 65; // 65 A字符的ascii码

  while (r < s.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    // isValidWindow, 长度在增长
    ct[get(r)]++;
    max = Math.max(max, ct[get(r)]);
    // !isValidWindow
    while (!isValidWindow()) {
      ct[get(l++)]--;
    }
    r++;
    // update result
    ans = Math.max(ans, r-l);
  }
  return ans;
};

3. 无重复字符的最长子串

/**
 * @param {string} s
 * @return {number}
 */
var lengthOfLongestSubstring = function(s) {
  if (!s.length) return 0;
  let l = 0, r = 0, ans = 0, ct = new Array(128).fill(0);
  const isValidWindow = () => ct[s.charCodeAt(r)] <= 1;

  while (r < s.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    const ch = s.charCodeAt(r);
    ct[ch]++;
    // !isValidWindow,由于重复字符可能出现在窗口中的任意位置，为了保持窗口的有效性，需要while循环右移窗口左侧边界直到窗口有效为止。
    while (!isValidWindow()) {
      ct[s.charCodeAt(l++)]--;
    }

    r++;
    ans = Math.max(ans, r - l);
  }
  return ans;
};

487. 最大连续1的个数 II

/**
 * @param {number[]} nums
 * @return {number}
 */
var findMaxConsecutiveOnes = function(nums) {
  let l = 0, r = 0, ans = 0, t0 = 0;
  while (r < nums.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    t0 += 1 - nums[r];
    // !isValidWindow, 每次的变化量不超过1，所以只需要右移窗口左边界一次就可以了，不需使用while循环。
    if (t0 > 1) {
      t0 -= 1 - nums[l++];
    }

    r++;
    // 条件更新result。
    if (t0 <= 1) {
      ans = Math.max(ans, r - l);
    }
  }
  return ans;
};

1004. 最大连续1的个数 III

给定一个由若干 0 和 1 组成的数组 A，我们最多可以将 K 个值从 0 变成 1 。
返回仅包含 1 的最长（连续）子数组的长度。

示例 1：
输入：A = [1,1,1,0,0,0,1,1,1,1,0], K = 2 输出：6 解释： [1,1,1,0,0,1,1,1,1,1,1] 粗体数字从 0 翻转到 1，最长的子数组长度为 6。
示例 2：
输入：A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3 输出：10 解释： [0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1] 粗体数字从 0 翻转到 1，最长的子数组长度为 10。

提示：

1. 1 <= A.length <= 20000
2. 0 <= K <= A.length

3. A[i] 为 0 或 1

   /**
   * @param {number[]} nums
   * @param {number} k
   * @return {number}
   */
   var longestOnes = function(nums, k) {
   let l = 0, r = 0, ans = 0, t0 = 0;
   while (r < nums.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    t0 += 1 - nums[r];
    // !isValidWindow, 每次的变化量不超过1，所以在k边界处只需要一次判断即可识别是否有效窗口，
    // 超过则说明窗口无效，所以只需要右移窗口左边界一次就可以了，不需使用while循环。
    if (t0 > k) {
      t0 -= 1 - nums[l++];
    }
   
    r++;
    if (t0 <= k) {
      ans = Math.max(ans, r - l);
    } 
   }
   return ans;
   };
   

   1695. 删除子数组的最大得分

   ```javascript // 使用set 判重。 /**

   • @param {number[]} nums
   • @return {number} */ var maximumUniqueSubarray = function(nums) { let l = 0, r = 0, ct = new Set(), s = 0, ans = 0; while (r < nums.length) { // isValidWindow, 由于一直是不重复，所以先最大化right，因此要使用while，直到找到一个重复的字符。 while (r < nums.length && !ct.has(nums[r])) { ct.add(nums[r]); s += nums[r++]; } // 前面的循环已经跳出，所以当前是非法的，update max result。 ans = Math.max(ans, s); // !isValidWindow, 窗口左边界右移，直至满足窗口 while (ct.has(nums[r])) { s -= nums[l]; ct.delete(nums[l++]); } } return ans; };

// 使用map计数方案： /**

• @param {number[]} nums
• @return {number} */ var maximumUniqueSubarray = function(nums) { let l = 0, r = 0, ct = new Map(), s = 0, ans = 0; while (r < nums.length) { ct.set(nums[r], ct.has(nums[r]) ? (1 + ct.get(nums[r])) : 1); s += nums[r]; while (ct.get(nums[r]) > 1) { s -= nums[l]; ct.set(nums[l], ct.get(nums[l]) - 1); l++; } r++; ans = Math.max(ans, s); } return ans; }; ```

  1208. 尽可能使字符串相等

  ```javascript /**
• @param {string} s
• @param {string} t
• @param {number} maxCost

• @return {number} */ var equalSubstring = function(s, t, maxCost) {

  // const arr = new Array(s.length).fill(0); // for (let i = 0; i < s.length;i++) { // arr[i] = Math.abs(s.charCodeAt(i) - t.charCodeAt(i)); // } let l = 0, r = 0, ans = 0, sum = 0; while (r < s.length) { // isValidWindow, 先最大化right，因此要使用while，直到成本消耗超过maxCost。 while (r < s.length && sum <= maxCost) { ans = Math.max(ans, r - l); sum += Math.abs(s.charCodeAt(r) - t.charCodeAt(r)); r++; } while (l < s.length && sum > maxCost) { sum -= Math.abs(s.charCodeAt(l) - t.charCodeAt(l)); l++; } } if (sum <= maxCost) { ans = Math.max(ans, r - l); } return ans; };

/**

• @param {string} s
• @param {string} t
• @param {number} maxCost
• @return {number} */ var equalSubstring = function(s, t, maxCost) { let l = 0, r = 0, ans = 0, sum = 0; while (r < s.length) { sum += Math.abs(s.charCodeAt(r) - t.charCodeAt(r)); while (l < s.length && sum > maxCost) { sum -= Math.abs(s.charCodeAt(l) - t.charCodeAt(l)); l++; } r++; if (sum <= maxCost) { ans = Math.max(ans, r - l); } } return ans; }; ```

  1493. 删掉一个元素以后全为 1 的最长子数组

  ```javascript 思路一：计算子数组前缀和，判断前缀和 与长度是否存在+1的关系。 /**
• @param {number[]} nums
• @return {number} */ var longestSubarray = function(nums) { let l = 0, r = 0, ans = Number.MIN_SAFE_INTEGER, t = 0; while (r < nums.length) { // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++ t += nums[r]; while (r-l + 1 > t + 1) { t -= nums[l++]; } r++; ans = Math.max(ans, r - l); } return ans === Number.MIN_SAFE_INTEGER ? 0 : ans-1; };

思路二：计算前缀和不超过1的最长子数组长度，最后再-1即可，注意特殊场景，数组全是0的场景，这是 前缀和和结果集都为1，则返回0. /**

• @param {number[]} nums
• @return {number} */ var longestSubarray = function(nums) { let l = 0, r = 0, ans = 0, t = 0; while (r < nums.length) { t += 1 - nums[r]; while (t > 1) { t -= 1 - nums[l++]; } r++; ans = Math.max(ans, r - l); } return t === ans ? 0 : ans - 1; }; ```

978. 最长湍流子数组

抄答案的正解，移动9中情况，排除两种情况：

1、A < B < C 排除，右移左指针到r - 1
2、A < B === C 排除，右移左指针到r
3、A < B > C 接受

4、A === B < C 接受
5、A === B === C 排除，右移左指针到r
6、A === B > C 接受

7、A > B < C 接受
8、A > B === C 排除，右移左指针到r
9、A > B > C 排除，右移左指针到r-1

简化为两种情况下需要排除：
一种的是前后两个变化一致， 1, 5、9
一种是当前数和上一个数相同，2、5、8

/**
 * @param {number[]} arr
 * @return {number}
 */
var maxTurbulenceSize = function(arr) {
  if (arr.length < 2) return 1;
  let ans = 0, r = 1, l = 0;
  const cp = (i) => {
    if (arr[i] > arr[i-1]) return 1;
    if (arr[i] === arr[i-1]) return 0;
    if (arr[i] < arr[i-1]) return -1;
  }
  let st = 0;
  while (r < arr.length) {
    const d = cp(r);
    // 前后两次变化率一致，增大、减小、不变。
    if (d === st) {
      l = r - 1;
    }
    // 和上一个数相同，直接跳过。
    if (arr[r - 1] === arr[r]) {
      l = r;
    }
    r++;
    ans = Math.max(ans, r - l);
    st = d;
  }
  return ans;
};

自己写的初始化AC版本和学习思路后，优化版本：

/**
 * @param {number[]} arr
 * @return {number}
 */
var maxTurbulenceSize = function(arr) {
  if (arr.length < 2) return 1;
  let ans = 0, r = 1, l = 0;
  const cp = (i) => {
    if (arr[i] > arr[i-1]) return 1;
    if (arr[i] === arr[i-1]) return 0;
    if (arr[i] < arr[i-1]) return -1;
  }
  // a > b => 1
  // a === b => 0
  // a < b => -1;
  let st = cp(1);
  while (r < arr.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    const d = cp(r);
    if (d * st !== -1) {
      l=r+1; // 为啥+1.跑前面去了？
    }
    r++;
    if (d * st === -1) {
      ans = Math.max(ans, r - l + 2);
    }
    st = d;
  }
  if (ans === 0 && st === 0) {
    return 1;
  }
  return Math.max(ans, r - l + 2);
};

按照第一个答案的思路优化下：

var maxTurbulenceSize = function(arr) {
  if (arr.length < 2) return 1;
  let ans = 0, r = 1, l = 0;
  const cp = (i) => {
    if (arr[i] > arr[i-1]) return 1;
    if (arr[i] === arr[i-1]) return 0;
    if (arr[i] < arr[i-1]) return -1;
  }
  // a > b => 1
  // a === b => 0
  // a < b => -1;
  let st = cp(1);
  while (r < arr.length) {
    // 窗口为[left, right], 所以每次要先判断窗口是否无效窗口，再right++
    const d = cp(r);
    // !== -1，代表除3，7外的所有场景，那么第一步就是，先从r-1开始。
    if (d * st !== -1) {
      l = r - 1;
      // l=r+1; // 为啥+1.跑前面去了？
    }
    // 再补充和前一个元素的相同的场景。2，5，8的处理逻辑，将l移动到r的位置
    if (arr[r] === arr[r - 1]) {
      l = r;
    }
    // 其他场景，1，2，5，8，9，经过上述两部处理后，长度最大为1，属于base case
    // 3，4，6，7 场景下，正常计算结果集大小。
    r++;
    ans = Math.max(ans, r - l);
    // if (d * st === -1) {
    // ans = Math.max(ans, r - l + 2);
    // }
    st = d;
  }
  return ans;
  // if (ans === 0 && st === 0) {
  //   return 1;
  // }
  // return Math.max(ans, r - l + 2);
};

计数

【distinct_and_equal(k)/计数/中等】1100. 长度为 K 的无重复字符子串

给你一个字符串 S，找出所有长度为 K 且不含重复字符的子串，请你返回全部满足要求的子串的 数目。
示例 1：

输入：S = “havefunonleetcode”, K = 5
输出：6
解释：
这里有 6 个满足题意的子串，分别是：’havef’,’avefu’,’vefun’,’efuno’,’etcod’,’tcode’。
示例 2：

输入：S = “home”, K = 5
输出：0
解释：
注意：K 可能会大于 S 的长度。在这种情况下，就无法找到任何长度为 K 的子串。

提示：

1 <= S.length <= 10^4
S 中的所有字符均为小写英文字母
1 <= K <= 10^4

/**
 * @param {string} s
 * @param {number} k
 * @return {number}
 */
var numKLenSubstrNoRepeats = function(s, k) {
  let l = 0, r = 0, ans = 0, c = new Array(26).fill(0), base = 'a'.charCodeAt(0);
  while (r < k && r < s.length) {
    c[s.charCodeAt(r++) - base]++;
  }


  // 这里效率不高，需要优化，可以使用一个ct 表示不同字符数量，当计数为1时，表示新增了一个字符，右移时退出窗口时，如果减为0，表示减少了一种字符。
  const isValidWindow = () => {
    // 字符不重复，
    let t = 0;
    for (let i = 0; i < c.length; i++) {
      if (c[i] === 0) continue;
      if (c[i] > 1) return false;
      if (c[i] === 1) {
        t++;
      }
    }
    return t === k;
  };
  if (isValidWindow()) {
    ans += 1;
  }
  while (r < s.length) {
    c[s.charCodeAt(r++) - base]++;
    c[s.charCodeAt(l++) - base]--;
    if (isValidWindow()) {
      ans += 1;
    }
  }
  return ans;
};

使用定长窗口的范式，然后，在window对象中实现窗口状态的维护。

/**
 * @param {string} s
 * @param {number} k
 * @return {number}
 */
var numKLenSubstrNoRepeats = function(s, k) {
  let l = 0, r = 0, ans = 0, win = new CharCounter(k);
  while (r < k && r < s.length) {
    win.add(s.charCodeAt(r++));
  }

  ans += win.countWin();
  while (r < s.length) {
    win.add(s.charCodeAt(r++));
    win.remove(s.charCodeAt(l++));
    ans += win.countWin();
  }
  return ans;
};

class CharCounter {
  constructor(k) {
    this.c = new Array(26).fill(0);
    this.ct = 0;
    this.k = k;
  }
  countWin() {
    return (this.ct === this.k) ? 1 : 0;
  }
  add(ch) {
    this.c[ch - 97]++;
    if (this.c[ch - 97] === 1) {
      this.ct++;
    }
  }
  remove(ch) {
    this.c[ch - 97]--;
    if (this.c[ch - 97] === 0) {
      this.ct--;
    }
  }
}

【distinct(2)/最长/中等】159. 至多包含两个不同字符的最长子串

难度中等131收藏分享切换为英文接收动态反馈
给定一个字符串 s ，找出 至多 包含两个不同字符的最长子串 t ，并返回该子串的长度。
示例 1:
输入: “eceba”
输出: 3
解释: t 是 “ece”，长度为3。

示例 2:
输入: “ccaabbb”
输出: 5
解释: t 是 “aabbb”，长度为5。

/**
 * @param {string} s
 * @return {number}
 */
var lengthOfLongestSubstringTwoDistinct = function(s) {
  let l = 0, r = 0, ct = new Array(128).fill(0), count = 0, ans = 0;
  while (r < s.length) {
    ct[s.charCodeAt(r)]++;
    if (ct[s.charCodeAt(r)] === 1) {
      count++;
    }
    r++;
    while (count === 3) {
      ct[s.charCodeAt(l)]--;
      if (ct[s.charCodeAt(l)] === 0) {
        count--;
      }
      l++;
    }
    ans = Math.max(ans, r - l);
  }
  return ans;
};

【distinct(k)/最长/中等】340. 至多包含 K 个不同字符的最长子串

难度中等145收藏分享切换为英文接收动态反馈
给定一个字符串 **_s_** ，找出 至多 包含 _k_ 个不同字符的最长子串 T。

示例 1:
输入: s = “eceba”, k = 2
输出: 3
解释: 则 T 为 “ece”，所以长度为 3。
示例 2:
输入: s = “aa”, k = 1
输出: 2
解释: 则 T 为 “aa”，所以长度为 2。

提示：

• 1 <= s.length <= 5 * 104
• 0 <= k <= 50

  /**
  * @param {string} s
  * @param {number} k
  * @return {number}
  */
  var lengthOfLongestSubstringKDistinct = function(s, k) {
  let l = 0, r = 0, ct = new Array(128).fill(0), ans = 0, count = 0;
  while (r < s.length) {
    ct[s.charCodeAt(r)]++;
    if (ct[s.charCodeAt(r)] === 1) {
      count++;
    }
    r++;
    while (count === k + 1) {
      ct[s.charCodeAt(l)]--;
      if (ct[s.charCodeAt(l)] === 0) {
        count--;
      }
      l++;
    }
    ans = Math.max(ans, r - l);
  }
  return ans;
  };
  

  【前缀和/差分/总量/困难】992. K 个不同整数的子数组

  难度困难310收藏分享切换为英文接收动态反馈
  给定一个正整数数组 A，如果 A 的某个子数组中不同整数的个数恰好为 K，则称 A 的这个连续、不一定不同的子数组为好子数组。
  （例如，[1,2,3,1,2] 中有 3 个不同的整数：1，2，以及 3。）
  返回 A 中好子数组的数目。
  
  示例 1：
  输入：A = [1,2,1,2,3], K = 2
  输出：7
  解释：恰好由 2 个不同整数组成的子数组：[1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].

示例 2：
输入：A = [1,2,1,3,4], K = 3
输出：3
解释：恰好由 3 个不同整数组成的子数组：[1,2,1,3], [2,1,3], [1,3,4].

提示：

1. 1 <= A.length <= 20000
2. 1 <= A[i] <= A.length
3. 1 <= K <= A.length

   /**
   * @param {number[]} nums
   * @param {number} k
   * @return {number}
   */
   var subarraysWithKDistinct = function(nums, k) {
   const atMost = (t) => {
    let l = 0, r = 0, ct = new Array(nums.length + 1).fill(0), c = 0, ans = 0;
    while (r < nums.length) {
      if (ct[nums[r++]]++ === 0) {
        c++;
      }
      while (c === t + 1) {
        if (--ct[nums[l++]] === 0) {
          c--;
        }
      }
      ans += r - l;
    }
    return ans;
   };
   return atMost(k) - atMost(k - 1);
   };
   

   【前缀积/差分/总量/中】713. 乘积小于K的子数组

   难度中等278收藏分享切换为英文接收动态反馈
   给定一个正整数数组 nums和整数 k 。
   请找出该数组内乘积小于 k 的连续的子数组的个数。
   
   示例 1:
   输入: nums = [10,5,2,6], k = 100
   输出: 8
   解释: 8个乘积小于100的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。
   需要注意的是 [10,5,2] 并不是乘积小于100的子数组。

示例 2:
输入: nums = [1,2,3], k = 0
输出: 0

提示:

• 1 <= nums.length <= 3 * 104
• 1 <= nums[i] <= 1000
• 0 <= k <= 106

  /**
  * @param {number[]} nums
  * @param {number} k
  * @return {number}
  */
  var numSubarrayProductLessThanK = function(nums, k) {
  let l = 0, r = 0, t = 1, ans = 0;
  while (r < nums.length) {
    t *= nums[r];
    while (l <= r && t >= k) {
      t /= nums[l++];
    }
    r++;
    ans += r - l;
  }
  return ans;
  };
  

  【distinct(k)/最长/中】904. 水果成篮

  在一排树中，第 i 棵树产生 tree[i] 型的水果。
  你可以从你选择的任何树开始，然后重复执行以下步骤：

1. 把这棵树上的水果放进你的篮子里。如果你做不到，就停下来。
2. 移动到当前树右侧的下一棵树。如果右边没有树，就停下来。

请注意，在选择一颗树后，你没有任何选择：你必须执行步骤 1，然后执行步骤 2，然后返回步骤 1，然后执行步骤 2，依此类推，直至停止。
你有两个篮子，每个篮子可以携带任何数量的水果，但你希望每个篮子只携带一种类型的水果。
用这个程序你能收集的水果树的最大总量是多少？

示例 1：
输入：[1,2,1]
输出：3
解释：我们可以收集 [1,2,1]。

示例 2：
输入：[0,1,2,2]
输出：3
解释：我们可以收集 [1,2,2]
如果我们从第一棵树开始，我们将只能收集到 [0, 1]。

示例 3：
输入：[1,2,3,2,2]
输出：4
解释：我们可以收集 [2,3,2,2]
如果我们从第一棵树开始，我们将只能收集到 [1, 2]。

示例 4：
输入：[3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：我们可以收集 [1,2,1,1,2]
如果我们从第一棵树或第八棵树开始，我们将只能收集到 4 棵水果树。

提示：

• 1 <= tree.length <= 40000

• 0 <= tree[i] < tree.length

  /**
  * @param {number[]} fruits
  * @return {number}
  */
  var totalFruit = function(fruits) {
  let l = 0, r = 0, ct = new Array(fruits.length + 1).fill(0), ans = 0, t = 0;
  while (r < fruits.length) {
    if (++ct[fruits[r++]] === 1) {
      t++;
    }
    while (t === 3) {
      if (--ct[fruits[l++]] === 0) {
        t--;
      }
    }
    ans = Math.max(ans, r - l);
  }
  return ans;
  };
  

  【distinct(k)/总量/中】1358. 包含所有三种字符的子字符串数目

  难度中等55收藏分享切换为英文接收动态反馈
  给你一个字符串 s ，它只包含三种字符 a, b 和 c 。
  请你返回 a，b 和 c 都 至少 出现过一次的子字符串数目。
  
  示例 1：
  输入：s = “abcabc”
  输出：10
  解释：包含 a，b 和 c 各至少一次的子字符串为 “_abc“, “abca“, “abcab“, “abcabc“, “bca“, “bcab“, “bcabc“, “cab“, “cabc“ 和 “abc“ (相同字符串算多次)。
  示例 2：
  输入：s = “aaacb”
  输出：3
  解释：包含 a，b 和 c 各至少一次的子字符串为 “aaacb“, “aacb“ 和 “acb“ 。_
  示例 3：
  输入：s = “abc”
  输出：1

  
  提示：

• 3 <= s.length <= 5 x 10^4

• s 只包含字符 a，b 和 c 。

  /**
  * @param {string} s
  * @return {number}
  */
  var numberOfSubstrings = function(s) {
  let l = 0, r = 0, ct = [0,0,0],t = 0,ans = 0, b = 'a'.charCodeAt(0);
  while (r < s.length) {
    if (++ct[s.charCodeAt(r++) - b] === 1) {
      t++;
    }
  
    while (t === 3) {
      // 关键点：由于后面的所有的都满足，所以不用遍历，直接计数，
      // 1, 表示[l, r)这一个，s.length - r 是后面的数字个数。
      ans += 1 + s.length - r;
      if (--ct[s.charCodeAt(l++) - b] === 0) {
        t--;
      }
    }
  }
  return ans;
  };
  

  【单调性/总量/中】467. 环绕字符串中唯一的子字符串

  难度中等160收藏分享切换为英文接收动态反馈
  把字符串 s 看作是“abcdefghijklmnopqrstuvwxyz”的无限环绕字符串，所以 s 看起来是这样的：”…zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd….”.
  现在我们有了另一个字符串 p 。你需要的是找出 s 中有多少个唯一的 p 的非空子串，尤其是当你的输入是字符串 p ，你需要输出字符串 s 中 p 的不同的非空子串的数目。
  注意: p 仅由小写的英文字母组成，p 的大小可能超过 10000。
  
  示例 1:
  输入: “a”
  输出: 1
  解释: 字符串 S 中只有一个”a”子字符。

  
  示例 2:
  输入: “cac”
  输出: 2
  解释: 字符串 S 中的字符串“cac”只有两个子串“a”、“c”。.

  
  示例 3:
  输入: “zab”
  输出: 6
  解释: 在字符串 S 中有六个子串“z”、“a”、“b”、“za”、“ab”、“zab”。. ```javascript /**

  • @param {string} p
  • @return {number} */ var findSubstringInWraproundString = function(p) { let r = 0, t = 0, ans = 0, ct = new Array(128).fill(0); while (r < p.length) { const diff = p.charCodeAt(r) - p.charCodeAt(r - 1); t = (diff === 1 || diff === -25) ? (t + 1) : 1; ct[p.charCodeAt(r)] = Math.max(t, ct[p.charCodeAt(r)]); r++; } for (let i = 0; i < 128; i++) { ans += ct[i]; } return ans; };

/**

• @param {string} p

• @return {number} */ var findSubstringInWraproundString = function(p) { let r = 0, t = 0, ans = 0, ct = new Array(128).fill(0); while (r < p.length) { let pre = p.charCodeAt(r - 1); let ch = p.charCodeAt(r++); const diff = ch - pre; t = (diff === 1 || diff === -25) ? (t + 1) : 1;

  ans -= ct[ch]; ct[ch] = Math.max(t, ct[ch]); ans += ct[ch]; } return ans; }; ```

  最小连续

模板：

let l = 0, r = 0, ans = 结果集
while (r < |len|) {
   更新窗口状态
   r++;
   while(l <= r && isWindow()) {
     更新结果集和状态
     l++;
   }
}
return ans;

76. 最小覆盖子串

难度困难1297收藏分享切换为英文接收动态反馈
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

• 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。

• 如果 s 中存在这样的子串，我们保证它是唯一的答案。

  
  示例 1：
  输入：s = “ADOBECODEBANC”, t = “ABC”
  输出：“BANC”

示例 2：
输入：s = “a”, t = “a”
输出：“a”

示例 3:
输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

• 1 <= s.length, t.length <= 105

• s 和 t 由英文字母组成

  /**
  * @param {string} s
  * @param {string} t
  * @return {string}
  */
  var minWindow = function(s, t) {
  let l = 0, r = 0, ct = new Array(128).fill(0) ;
  while (l < t.length) {
    const ch = t.charCodeAt(l++);
    ct[ch]++;
  }
  l = 0; temp = new Array(128).fill(0);
  let ans="";
  
  const isValidWindow = (win) => {
    for (let i = 0; i < ct.length; i++) {
      if (ct[i] === 0) continue;
      // 窗口中字符计数比统计结果少，窗口无效。
      if (win[i] < ct[i]) return false;
    }
    return true;
  };
  while (r < s.length) {
    // 无效字符过滤。
    if (ct[s.charCodeAt(r)] === 0) {
      r++;
      continue;
    }
    // 首先无效窗口时，右指针右移
    temp[s.charCodeAt(r++)]++;
    // 窗口有效时，左指针右移
    while (l < s.length && isValidWindow(temp)) {
      // 更新结果
      if (ans.length === 0 || (r - l) < ans.length) {
        ans = s.substring(l, r);
      }
      temp[s.charCodeAt(l++)]--;
    }
  }
  return ans;
  };
  

  209. 长度最小的子数组

  /**
  * @param {number} target
  * @param {number[]} nums
  * @return {number}
  */
  var minSubArrayLen = function(target, nums) {
  let l = 0, r = 0, s = 0, ans = Number.MAX_SAFE_INTEGER;
  while (r < nums.length) {
    s += nums[r++];
    while (l < nums.length && s >= target) {
      ans = Math.min(ans, r - l);
      s -= nums[l++];
    }
  }
  return ans === Number.MAX_SAFE_INTEGER ? 0 : ans;
  };
  

  【子序列/困难】727. 最小窗口子序列

  难度困难91收藏分享切换为英文接收动态反馈
  给定字符串 S and T，找出 S 中最短的（连续）子串 W ，使得 T 是 W 的 子序列 。
  如果 S 中没有窗口可以包含 T 中的所有字符，返回空字符串 ""。如果有不止一个最短长度的窗口，返回开始位置最靠左的那个。
  示例 1：
  输入：
  S = “abcdebdde”, T = “bde”
  输出：“bcde”
  解释：
  “bcde” 是答案，因为它在相同长度的字符串 “bdde” 出现之前。
  “deb” 不是一个更短的答案，因为在窗口中必须按顺序出现 T 中的元素。
  
  注：

• 所有输入的字符串都只包含小写字母。All the strings in the input will only contain lowercase letters.

• S 长度的范围为 [1, 20000]。
• T 长度的范围为 [1, 100]。

必须有序，所以无法使用计数方式来检测窗口是否满足。只能用双指针来扫描两个字符串。

/**
 * @param {string} s1
 * @param {string} s2
 * @return {string}
 */
var minWindow = function(s1, s2) {
  let l = 0, r = 0, ans = '';
  const update = (pos) => {
    let start = pos;
    while (r > 0) {
      if (s1.charAt(start--) === s2.charAt(r-1)) {
        r--;
      }
    }
    start++; // s1 中结果区间范围：[start, l]
    return start;
  };

  while (l < s1.length) {
    if (s1.charAt(l) === s2.charAt(r)) {
      r++;
    }
    if (r === s2.length) {
      let nextL = update(l);
      if (l - nextL + 1 < ans.length || ans.length === 0) {
        ans = s1.substring(nextL, l + 1);
      }
      l = nextL;
      r = 0;
    }
    l++;
  }
  return ans;
};

【重要】995. K 连续位的最小翻转次数

难度困难205收藏分享切换为英文接收动态反馈
在仅包含 0 和 1 的数组 A 中，一次 _K_ 位翻转包括选择一个长度为 K 的（连续）子数组，同时将子数组中的每个 0 更改为 1，而每个 1 更改为 0。
返回所需的 K 位翻转的最小次数，以便数组没有值为 0 的元素。如果不可能，返回 -1。

示例 1：
输入：A = [0,1,0], K = 1
输出：2
解释：先翻转 A[0]，然后翻转 A[2]。

示例 2：
输入：A = [1,1,0], K = 2
输出：-1
解释：无论我们怎样翻转大小为 2 的子数组，我们都不能使数组变为 [1,1,1]。

示例 3：
输入：A = [0,0,0,1,0,1,1,0], K = 3
输出：3
解释：
翻转 A[0],A[1],A[2]: A变成 [1,1,1,1,0,1,1,0]
翻转 A[4],A[5],A[6]: A变成 [1,1,1,1,1,0,0,0]
翻转 A[5],A[6],A[7]: A变成 [1,1,1,1,1,1,1,1]

提示：

1. 1 <= A.length <= 30000
2. 1 <= K <= A.length

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var minKBitFlips = function(nums, k) {
  let ans = 0;
  for (let r = 0; r < nums.length; r++) {
    if (nums[r] === 0) {
      if (r + k > nums.length)  return -1;
      let j = 0;
      while (j < k) {
        nums[r + j] = 1 - nums[r + j];
        j++;
      }
      ans += 1;
    }
  }
  return ans;
};

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var minKBitFlips = function(nums, k) {
  let ans = 0;
  for (let r = 0; r < nums.length; r++) {
    if (nums[r] === 0) {
      if (r + k > nums.length)  return -1;
      let j = 0;
      while (j < k) {
        nums[r + j++] ^= 1;
      }
      ans += 1;
    }
  }
  return ans;
};

其他解法：

方法一：滑动窗口 fuxuemingzhu

上面方法超时的主要原因是我们真实地进行了翻转。根据结论二，位置 ii 现在的状态，和它被前面 K - 1K−1 个元素翻转的次数（奇偶性）有关。

我们使用队列模拟滑动窗口，该滑动窗口的含义是前面 K - 1K−1 个元素中，以哪些位置起始的 子区间 进行了翻转。该滑动窗口从左向右滑动，如果当前位置 ii 需要翻转，则把该位置存储到队列中。遍历到新位置 j (j < i + K)j(j<i+K) 时，队列中元素的个数代表了 ii 被前面 K - 1K−1 个元素翻转的次数。

当 A[i]A[i] 为 0，如果 ii 位置被翻转了偶数次，那么翻转后仍是 0，当前元素需要翻转；
当 A[i]A[i] 为 1，如果 ii 位置被翻转了奇数次，那么翻转后变成 0，当前元素需要翻转。
综合上面两点，我们得到一个结论，如果 len(que) % 2 == A[i] 时，当前元素需要翻转。

当 i + K > Ni+K>N 时，说明需要翻转大小为 K 的子区间，但是后面剩余的元素不到 K 个了，所以返回 -1。

示例
下面的动图演示了题目给出的示例三 A = [0,0,0,1,0,1,1,0], K = 3 的情况：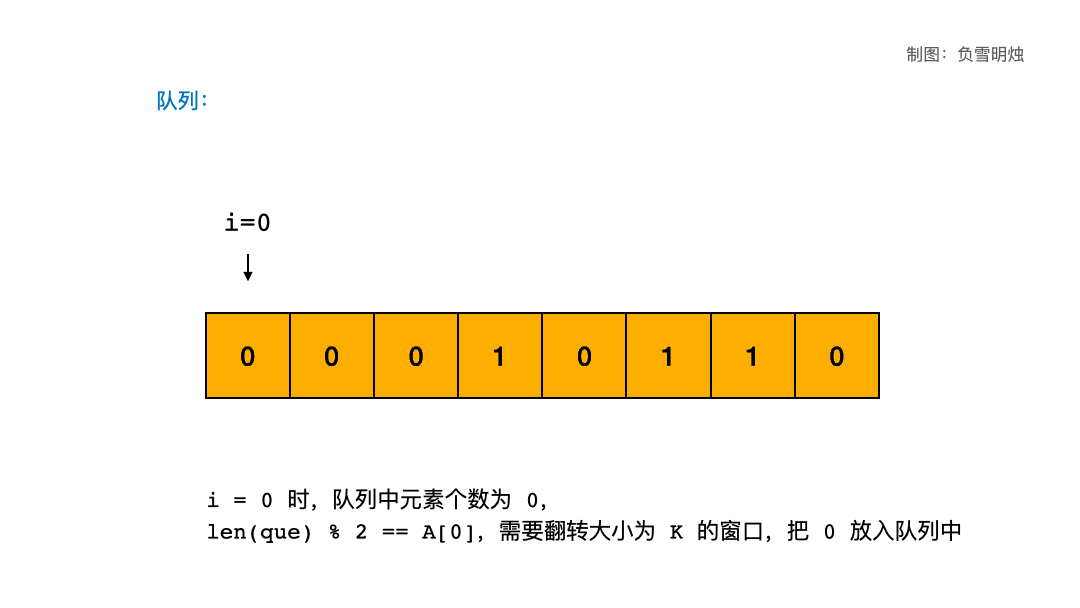

class Solution {
public:
    int minKBitFlips(vector<int>& A, int K) {
        int N = A.size();
        queue<int> que;
        int res = 0;
        for (int i = 0; i < N; ++i) {
            if (!que.empty() && i >= que.front() + K) {
                que.pop();
            }
            if (que.size() % 2 == A[i]) {
                if (i + K > N) {
                    return -1;
                }
                que.push(i);
                res ++;
            }
        }
        return res;
    }
};

方法二：滑动窗口 官解

能否将空间复杂度优化至 O(1) 呢？
回顾方法一的代码，当遍历到位置i 时，若能知道位置 i−k上发生了翻转操作，便可以直接修改revCnt，从而去掉 diff 数组。
注意到 0≤nums[i]≤1，我们可以用 nums[i] 范围之外的数来表达「是否翻转过」的含义。

具体来说，若要翻转从位置i开始的子数组，可以将 nums[i] 加 2，这样当遍历到位置 i′时，若有 nums[i′−k]>1，则说明在位置 i′−k 上发生了翻转操作。

时间复杂度：O(n)。其中 nn 是数组nums 的长度。需要对数组nums 遍历一次。

空间复杂度：O(1)。

var minKBitFlips = function(nums, k) {
    const n = nums.length;
    let ans = 0, revCnt = 0;
    for (let i = 0; i < n; ++i) {
        if (i >= k && nums[i - k] > 1) {
            revCnt ^= 1;
            nums[i - k] -= 2; // 复原数组元素，若允许修改数组 nums，则可以省略
        }
        if (nums[i] == revCnt) {
            if (i + k > n) {
                return -1;
            }
            ++ans;
            revCnt ^= 1;
            nums[i] += 2;
        }
    }
    return ans;
};

方法三：一次遍历，常数空间，面对困难题也要重拳出击

因为题目给了 K 大小反转窗口，所以我们可以尝试应用滑动窗口。通过观察，我们可以隐约发现，每次应该在第一个 0 元素位置开始反转，如果能够使得整个数组不存在 0，即返回res作为反转次数。

此题有几个小诀窍可以应用：

1. 当反转次数为奇数次，元素会由 0 -> 1，1 -> 0; 当反转次数为偶数次，元素不变;
   2. 由于我们关注窗口的起点，所以我们可以在处理过的元素中 +2 ，这样可以标记反转窗口起始点；
   3. 同时我们还需要关注同一元素在窗口内反转了几次，用 windowFlip 表示。这样的话如果元素为 0，则满足 windowFlip % 2 == A[i]

public int minKBitFlips(int[] A, int K) {
    int len = A.length, res = 0, windowFlip = 0;
    for (int i = 0; i < len; i++) {
        if (i - K >= 0 && A[i - K] > 1) { // 找到反转起始点，要跟下方标记点对应好
            windowFlip--; 
        } 
        if (windowFlip % 2 == A[i]) { //反转奇数次后是1 或者 反转偶数次后是0
            if (i + K - 1 >= len) 
                return -1;
            A[i] += 2; // 标记反转起始点，加几随意
            windowFlip++; 
            res++;
        }

    }
    return res;
}

方法四：贪心 + 差分解法

由于我们总是对连续的一段进行「相同」的操作，同时只有「奇数」次数的翻转才会真正改变当前位置上的值。

自然而然，我们会想到使用数组 arr 来记录每一位的翻转次数。

同时我们又不希望是通过「遍历记 arr 的 k 位进行 +1」来完成统计。

因此可以使用差分数组来进行优化：当需要对某一段 [l,r] 进行 +1 的时候，只需要 arr[l]++ 和 arr[r + 1]— 即可。

class Solution {
    public int minKBitFlips(int[] nums, int k) {
        int n = nums.length;
        int ans = 0;
        int[] arr = new int[n + 1];
        for (int i = 0, cnt = 0; i < n; i++) {
            cnt += arr[i];
            if ((nums[i] + cnt) % 2 == 0) {
                if (i + k > n) return -1;
                arr[i + 1]++;
                arr[i + k]--;
                ans++;
            }
        }
        return ans;
    }
}

【重要】二段性

395. 至少有 K 个重复字符的最长子串

难度中等538收藏分享切换为英文接收动态反馈
给你一个字符串 s 和一个整数 k ，请你找出 s 中的最长子串， 要求该子串中的每一字符出现次数都不少于 k 。返回这一子串的长度。

示例 1：
输入：s = “aaabb”, k = 3 输出：3 解释：最长子串为 “aaa” ，其中 ‘a’ 重复了 3 次。
示例 2：
输入：s = “ababbc”, k = 2 输出：5 解释：最长子串为 “ababb” ，其中 ‘a’ 重复了 2 次， ‘b’ 重复了 3 次。

提示：

• 1 <= s.length <= 104
• s 仅由小写英文字母组成
• 1 <= k <= 105

抄答案：

/**
 * @param {string} s
 * @param {number} k
 * @return {number}
 */
var longestSubstring = function(s, k) {
  let ans = 0;
  for (let i = 0; i < 26; i++) {
    let l = 0, r = 0, ct = new Array(26).fill(0);
    let type = 0, mtype = 0;
    while (r < s.length) {
      let ch = s.charCodeAt(r++) - 97;
      ct[ch]++;
      if (ct[ch] === 1) {
        type++;
      }
      if (ct[ch] === k) {
        mtype++;
      }

      while (type > i) {
        let lch = s.charCodeAt(l++) - 97;
        ct[lch]--;
        if (ct[lch] === 0) {
          type--;
        }
        if (ct[lch] === k -1) {
          mtype--;
        }
      }
      if (type === mtype) {
        ans = Math.max(ans, r - l);
      }
    }
  }
  return ans;
};

https://leetcode-cn.com/problems/longest-substring-with-at-least-k-repeating-characters/solution/xiang-jie-mei-ju-shuang-zhi-zhen-jie-fa-50ri1/
其实看到这道题，我第一反应是「二分」，直接「二分」答案。

但是往下分析就能发现「二分」不可行，因为不具有二段性质。

也就是假设有长度 t 的一段区间满足要求的话，t + 1 长度的区间是否「一定满足」或者「一定不满足」呢？

显然并不一定，是否满足取决于 t + 1 个位置出现的字符在不在原有区间内。

举个🌰吧，假设我们已经画出来一段长度为 t 的区间满足要求（且此时 k > 1），那么当我们将长度扩成 t + 1 的时候（无论是往左扩还是往右扩）：

如果新位置的字符在原有区间出现过，那必然还是满足出现次数大于 k，这时候 t + 1 的长度满足要求
如果新位置的字符在原有区间没出现过，那新字符的出现次数只有一次，这时候 t + 1 的长度不满足要求
因此我们无法是使用「二分」，相应的也无法直接使用「滑动窗口」思路的双指针。

因为双指针其实也是利用了二段性质，当一个指针确定在某个位置，另外一个指针能够落在某个明确的分割点，使得左半部分满足，右半部分不满足。

那么还有什么性质可以利用呢？这时候要留意数据范围「数值小」的内容。

题目说明了只包含小写字母（26 个，为有限数据），我们可以枚举最大长度所包含的字符类型数量，答案必然是 [1, 26]，即最少包含 1 个字母，最多包含 26 个字母。

你会发现，当确定了长度所包含的字符种类数量时，区间重新具有了二段性质。

当我们使用双指针的时候：

右端点往右移动必然会导致字符类型数量增加（或不变）
左端点往右移动必然会导致字符类型数量减少（或不变）
当然，我们还需要记录有多少字符符合要求（出现次数不少于 k），当区间内所有字符都符合时更新答案。

class Solution {
    public int longestSubstring(String s, int k) {
        int ans = 0;
        int n = s.length();
        char[] cs = s.toCharArray();
        int[] cnt = new int[26];
        for (int p = 1; p <= 26; p++) {
            Arrays.fill(cnt, 0);
            // tot 代表 [j, i] 区间所有的字符种类数量；sum 代表满足「出现次数不少于 k」的字符种类数量
            for (int i = 0, j = 0, tot = 0, sum = 0; i < n; i++) {
                int u = cs[i] - 'a';
                cnt[u]++;
                // 如果添加到 cnt 之后为 1，说明字符总数 +1
                if (cnt[u] == 1) tot++;
                // 如果添加到 cnt 之后等于 k，说明该字符从不达标变为达标，达标数量 + 1
                if (cnt[u] == k) sum++;
                // 当区间所包含的字符种类数量 tot 超过了当前限定的数量 p，那么我们要删除掉一些字母，即「左指针」右移
                while (tot > p) {
                    int t = cs[j++] - 'a';
                    cnt[t]--;
                    // 如果添加到 cnt 之后为 0，说明字符总数-1
                    if (cnt[t] == 0) tot--;
                    // 如果添加到 cnt 之后等于 k - 1，说明该字符从达标变为不达标，达标数量 - 1
                    if (cnt[t] == k - 1) sum--;
                }
                // 当所有字符都符合要求，更新答案
                if (tot == sum) ans = Math.max(ans, i - j + 1);
            }
        }
        return ans;
    }
}

作者：AC_OIer
链接：https://leetcode-cn.com/problems/longest-substring-with-at-least-k-repeating-characters/solution/xiang-jie-mei-ju-shuang-zhi-zhen-jie-fa-50ri1/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。