零、⼆分查找框架

def binarySearch(self, nums,target):
    left = 0
    right = ...    # 注意
    while ...:
        mid =  (left + (right - left)) // 2
        if nums[mid] > target:
            ...
        elif nums[mid] < target:
            ...
        elif nums[mid] == target:
            ...
     return ...

⼀、寻找⼀个数（基本的⼆分搜索）

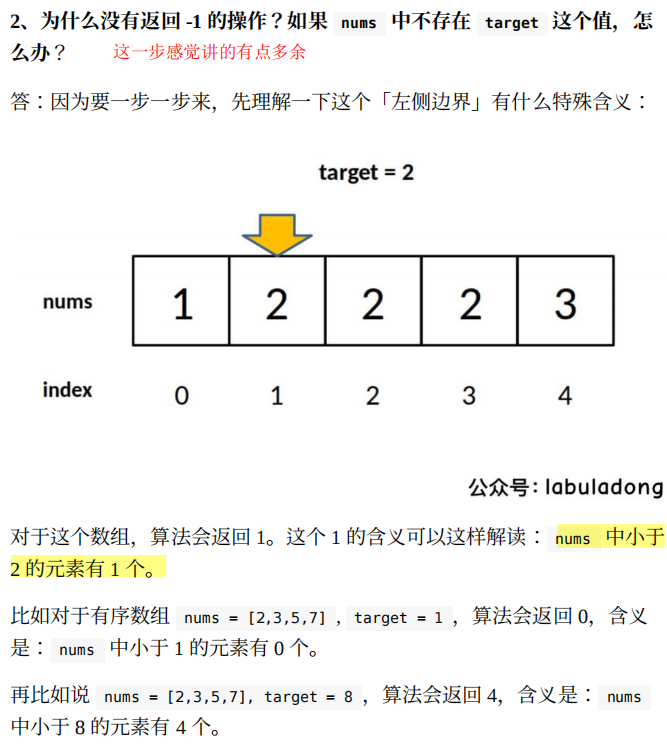
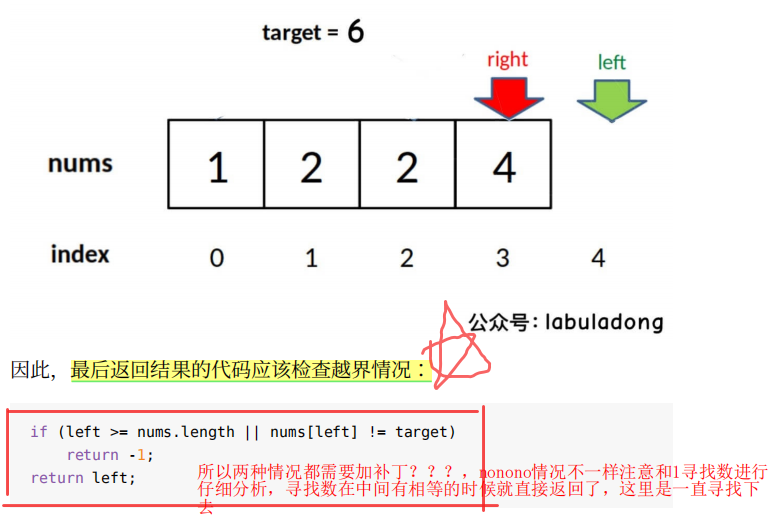
⼆、寻找左侧边界的⼆分搜索

三、寻找右侧边界的⼆分查找

四、逻辑统⼀

练习题目

剑指 Offer 11. 旋转数组的最小数字

class Solution:
    def minArray(self, numbers: [int]) -> int:
        i, j = 0, len(numbers) - 1
        while i < j:
            m = (i + j) // 2
            if numbers[m] > numbers[j]: i = m + 1
            elif numbers[m] < numbers[j]: j = m
            else: j -= 1
        return numbers[i]

实际上，当出现 nums[m] = nums[j]nums[m]=nums[j] 时，一定有区间 [i, m]内所有元素相等 或 区间 [m,j] 内所有元素相等（或两者皆满足）。对于寻找此类数组的最小值问题，可直接放弃二分查找，而使用线性查找替代。

class Solution:
    def minArray(self, numbers: [int]) -> int:
        i, j = 0, len(numbers) - 1
        while i < j:
            m = (i + j) // 2
            if numbers[m] > numbers[j]: i = m + 1
            elif numbers[m] < numbers[j]: j = m
            else: return min(numbers[i:j])
        return numbers[i]